Функции радиального базиса (пример)

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Функция радиального базиса — функция, значение которой зависит только от нормы аргумента. RBF используются в метрических алгоритмах классификации, в частности в методе потенциальных функций, который (в упрощенном виде) рассматривается в этой статье.

Содержание

1 Постановка задачи
2 Ядерные функции
3 Алгоритм отыскания оптимальных параметров
4 Вычислительный эксперимент
5 Исходный код
6 Смотри также
7 Литература

Постановка задачи

Задана выборка $X^l$ , в которой описание каждого объекта является вектором $x_{i}\in R^n$ . Метки классов $y_i$ принадлежат множеству $Y=\{+1,-1\}$ . Считается, что каждый объект выборки $x_i$ имеет некоторый «заряд» $\gamma_i$ и создает в пределах окрестности $h_i$ потенциал, вид которого определяется функцией радиального базиса $K(x)$ . Таким образом, суммарный потенциал в точке $x\in{R^n}$ определяется по формуле:

$\phi(x)=\sum_{y=1}^{l}{y_{i}\gamma_{i}K(\frac{x_i-x}{h_i})}.$

Знак этого потенциала определяет класс объекта $x$ , т.е. классификатор $a(x)={\rm sign}\nolimits \phi(x)$ . Требуется оптимизировать значения параметров $\gamma_i$ , $h_i$ .

Ядерные функции

Одной из важных частей алгоритма является выбор функции радиального базиса $K(x)$ . В качестве $K$ могут применяться следующие функции (введено обозначение $\|x\|=r$ ):

Гауссиана $G(x)=\exp(-\beta r^2)$ , где $\beta>0$ .
Ядро логистической регрессии $L(x)=\frac{1}{1+e^{r/\sigma}}$ , $\sigma>0$ .
Ядро, соответсвующее ньютонову потенциалу $N(x)=\frac{1}{A+r}$ , $A>0$ .
Модифицированный ньютонов потенциал $N_n(x)=\frac{1}{A+r^n}$ , $A>0$ , $n>0$ .
Треугольное ядро $T(x)=(1-r)[r\leq 1]$ .
Модифицированное треугольное ядро $T_n(x)=(1-r)^{n}[r\leq 1]$ , $n>0$ .
Прямоугольное ядро $P(x)=[r\leq 1]$ .
Ядро Епанечникова $E(x)=(1-r^2)[r\leq 1]$ .
Квартическое ядро $Q(x)=(1-r^2)^2[r\leq 1]$ .
Обобщенное квартическое ядро $Q_n(x)=(1-r^2)^n[r\leq 1]$ , $n>0$ .
Обратное мультиквадратичное ядро $M(x)=\frac{1}{\sqrt{A+r^2}}$ , $A>0$ .
Семейство ядер Вендланда $W_{nl}$ , представляющее собой многочлены на отрезке $[-1,+1]$ и равные

нулю вне его. Они характеризуются двумя параметрами — размерностью пространства $n$ и степенью гладкости $l$ . В данной реализации используется первые девять ядер:

$n$	$l$	$W_{nl}$
1	0	$(1-r)_{+}$
1	2	$(1-r)^{3}_{+}(3r+1)$
1	4	$(1-r)^{5}_{+}(8r^2+5r+1)$
3	0	$(1-r)^{2}_{+}$
3	2	$(1-r)^{4}_{+}(4r+1)$
3	4	$(1-r)^{6}_{+}(7r^2+6r+1)$
5	0	$(1-r)^{3}_{+}$
5	2	$(1-r)^{5}_{+}(5r+1)$
5	4	$(1-r)^{7}_{+}(16r^2+7r+1)$

Используется обозначение $F_{+}=\max(0, F)$ .

Алгоритм отыскания оптимальных параметров

Считается, что радиусы всех потенциалов равны между собой ( $h_i=h$ $\forall i=1,...,l$ ). Переменная $h$ , а также параметры RBF (если таковые имеются) — структурные параметры метода. Заряды $\gamma_i$ настраиваются согласно алгоритму:

положить $\gamma_i:=0$ $\forall i=1,...,l$ .
повторять
выбрать случайный элемент из выборки
если $a(x_i)\neq y_i$ то
$\gamma_i:=\gamma_i+1$
пока не выполнен критерий останова

Используются следующие критерии останова алгоритма:

Ограничение на максимальное количество итераций.
Доля ошибок на обучающей выборке — если $\sum_{i=1}^l{[y_i\neq a(x_i)]} < \varepsilon$ , то алгоритм останавливается. $\varepsilon$ является структурным параметром метода.
В качестве развития предыдущего пункта — процент ошибок на тестовой выборке $X^k$ , которая

выделяется из обучающей заранее случайным образом. Доля объектов, которые войдут в тестовую выборку, задается извне.

Поскольку подсчет доли ошибок — весьма трудоемкий процесс, то рационально выполнять его не в каждой итерации алгоритма. Частоту проверок можно изменять извне.

Вычислительный эксперимент

Для проверки работоспособности алгоритма использовались наборы реальных и синтетических данных.

1) Реальные данные

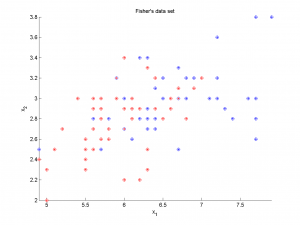
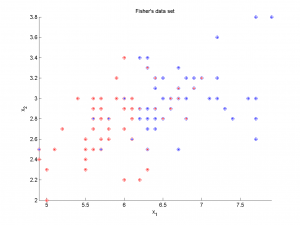
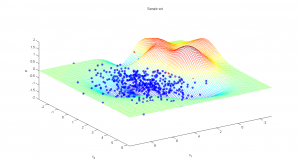
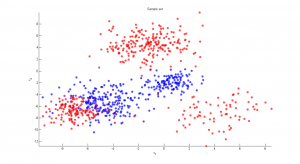
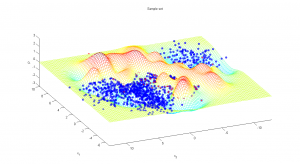
В качестве реальных данных использовались данные о сортах ирисов, собранные Фишером. Обучающая выборка состояла из 100 объектов (по 50 объектов каждого из двух классов), обладающих четырьмя вещественными признаками. При использовании всех четырех признаков алгоритм показал очень хороший результат, неправильно классифицировав три объекта. При использовании только первых двух признаков классы глубоко проникают друг в друга; алгоритм работает значительно хуже, неправильно классифицируя около 25 объектов.

По осям графиков отложены значения признаков. Точки — объекты, цвет точек обозначает принадлежность к тому или иному классу; цвет кружков вокруг точек — результат работы алгоритма.

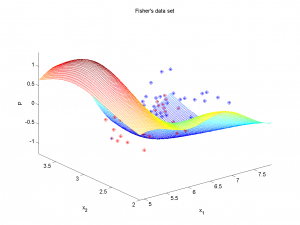
Во втором случае возможно нарисовать трехмерный график, изображающий потенциал в различных точках пространства признаков:

2) Синтетические данные

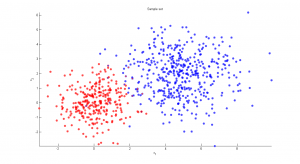
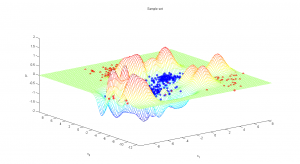
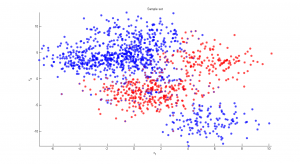
Синтетические данные представляли собой объекты с двумя признаками из нескольких кластеров. В пределах каждого из кластеров признаки имели нормальное распределение. В зависимости от числа кластеров и параметров распределения задача классификации представляла разную сложность.

baseL = 200;   %average number of objects in clusters
X = [];
y = [];
L = 0;
CLUSTERS = 5;  %number of clusters
for cl=1:CLUSTERS
    alpha = 0.5 + rand; 
    L2 = floor(baseL*alpha); %number of objects in the cluster
    sigma = 1 + 1.5*rand;  %variance of feature values
    dist = 3 + 5*rand;   %distance to the (0, 0) point
    v = repmat(...
        dist * [sin(2*pi*rand) cos(2*pi*rand)], ...
        [L2, 1]);   %random vector between (0, 0) and the center of the cluster
    X2 = sigma * randn(L2, 2) + v; %objects in cluster
    label = sign(rand-0.5);  %choosing class of objects
    if (label == 0)
        label = 1;
    end
    X = [X; X2];
    y = [y; repmat(label, [L2, 1])];
    L = L + L2; %L is total number of objects
end

2.1) Легкий случай

Объекты формируют два кластера со слабым взаимным проникновением. Качество классификации хорошее (меньше 5% неправильно определенных меток классов).

2.2) Промежуточный случай

Объекты составляют пять кластеров с существенным проникновением. Неправильно классифицировано около 8% объектов.

2.3) Сложный случай

Объекты составляют восемь кластеров с сильным проникновением друг в друга. Неправильно классифицировано около 13% объектов.

Исходный код

kernel.m, rbflearn.m, rbfmdl.m - (реализация алгоритма); demo_kernel.m - (демонстрация доступных ядер); demo_iris.m, demo_synth1.m, demo_synth2.m - (вычислительный эксперимент).

Смотри также

Литература

К. В. Воронцов. Лекции по метрическим алгоритмам классификации.
Хардле В. Прикладная непараметрическая регрессия.
Интерактивная помощь программы MATLAB.
Bishop C. Pattern Recognition and Machine Learning.

Данная статья была создана в рамках учебного задания.

Студент: Участник:Алексей Островский

Преподаватель: Участник:В.В. Стрижов

Срок: 28 мая 2009

В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A4%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B8_%D1%80%D0%B0%D0%B4%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE_%D0%B1%D0%B0%D0%B7%D0%B8%D1%81%D0%B0_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категории: Метрические алгоритмы классификации | Практика и вычислительные эксперименты

@@ Строка 55: / Строка 55: @@
 | 3 || 2 || <tex>(1-r)^{4}_{+}(4r+1)</tex>
 |-
-| 3 || 4 || <tex>(1-r)^{6}_{+}(35r^2+18r+3)</tex>
+| 3 || 4 || <tex>(1-r)^{6}_{+}(7r^2+6r+1)</tex>
 |-
 | 5 || 0 || <tex>(1-r)^{3}_{+}</tex>

Функции радиального базиса (пример)

Материал из MachineLearning.

Текущая версия

Содержание

Постановка задачи

Ядерные функции

Алгоритм отыскания оптимальных параметров

Вычислительный эксперимент

Исходный код

Смотри также

Литература

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты