Прогнозирование плотности транспортного потока

Материал из MachineLearning.

(Различия между версиями)

Перейти к: навигация, поиск

Текущая версия

Данная статья была создана в рамках учебного задания.

Студент: Петров Г.Е.

Преподаватель: Чехович Ю.В.

Срок:

В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Прогнозирование плотности транспортных потоков.

Содержание

1 Общее описание
2 Постановка задачи
3 Решение задачи
4 Вычислительный эксперимент
- 4.1 Значения параметров
- 4.2 Результат
5 Заключение
6 Литература

Общее описание

Введем понятия и обозначения, которые в дальнейшем будут использованы в статье: АТС — автомобильное транспортное средство; $\rho(t,x)$ — число АТС на единицу длины в момент времени $t$ в окрестности точки трассы с координатой $x$ (плотность транспортного потока); $v(t,x)$ — скорость АТС в момент времени $t$ в окрестности точки трассы с координатой $x$ ; $Q(\rho)$ — количество АТС, проходящих в единицу времени через заданное сечение (интенсивность транспортного потока).

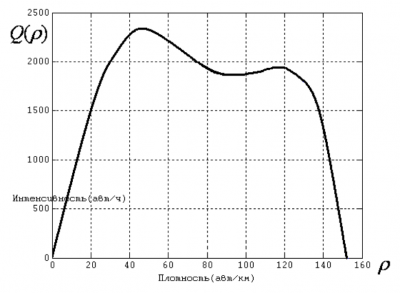
Зависимость $Q(\rho)$ также часто называют фундаментальной (основной) диаграммой. Обычно данная зависимость выглядит следующим образом:

Фундаментальная диаграмма

Провал интенсивности потока при плотностях $\rho \sim 60-115$ шт/км можно тем, что в этом случае на интенсивность потока существенно влияют перемещения АТС между полосами.

Для измерения различных характеристик и определения дорожной ситуации в конкретном ее месте устанавливают транспортные детекторы. Они могут собирать такие данные, как индивидуальная скорость АТС, количество АТС, заполненность (отношение количества времени, когда автомобиль находился под транспортным детектором, к общему времени измерения). Очевидно, минусом такого подхода является то, что все показатели известны только в определенной точке дороги.

Вторым важным подходом для определения дорожной ситуации является использование GPS-трекеров, которые широко распространены в последнее время. Минусами такого подхода являются погрешности измерения приборов и относительно невысокий процент оборудованных ими АТС.

Замечание. Все измерения производятся в системе СИ, если не оговорено иначе.

Постановка задачи

На графе дорог в известных точках установлены детекторы, которые измеряют среднюю скорость потока и заполненность. Некоторая часть АТС оборудована GPS-трекерами. Требуется придумать алгоритм, который в каждый момент времени будет наилучшим образом определять плотность транспортного потока на всех ребрах графа дорог. Насколько увеличится ошибка определения плотности, если есть ошибка в исходных данных: как в треках GPS-трекеров (положение автомобиля меняется в круге радиуса $R$ ), так и в данных детекторов? Каким образом лучше всего расположить детекторы для минимизации ошибки определения плотности?

Также возникает ряд других интересных задач, которые будут описаны ниже по мере их появления.

Решение задачи

Описание конфигурации

Опишем все необходимые параметры, которые будут в дальнейшем использоваться для эксперимента.

Рассмотрим однополосную кольцевую дорогу с радиусом $R$ . Пусть все параметры объектов, участвующих в транспортной системе, пересчитываются с периодом $t_{\mathit{iter}}$ (период дискретизации); $t_{\mathit{a}}$ — период обновления положения АТС; $t_{\mathit{d}\mathit{et}}$ — период обновления собранной детектором статистики по дорожной ситуации. Пусть также на дороге расположены объекты: множество светофоров $TL$ , у которых определены время горения зеленого света $t_{\mathit{green}}$ и красного света $t_{\mathit{red}}$ ; множество детекторов $D$ ; множество АТС $A$ . Изначально все АТС расположены друг за другом на одинаковом расстоянии.

Измерение качества

Как уже было отмечено выше, существуют несколько вариантов получения неточных измерений:

погрешность измерения детектора;
погрешность измерения GPS-трекера;
погрешность работы самого алгоритма.

Для более точного подбора подходящего алгоритма решения задачи необходимо минимизировать ошибки первых двух типов, поэтому реальные данные не подходят для анализа. Этот факт следует из тех соображений, что в случае возникновения большой ошибки вычисления плотности транспортного потока неясно, что является ее источником: ошибочные показания детектора, высокая погрешность GPS-трекера или же ошибки самого алгоритма. В связи с этим возникает необходимость в генерации искусственных данных и в варьировании параметров, которые применялись при генерации, для определения зависимости точности работы алгоритма от входных данных. Также в этом случае можно точно определить все интересующие характеристики транспортной системы, так как в любой момент можно их измерить. В реальной же ситуации такой возможности нет: есть лишь исторические данные, собранные с помощью неточных приборов.

Для измерения качества определения плотности транспортного потока выберем интересующий нас участок дороги длиной $L$ метров. В течение всего времени $T$ симуляции дорожного движения будем измерять плотность на этом участке и строить график ее зависимости от времени. Для определения ошибки измерения плотности потока методом №1 относительно метода №2 будем использовать формулу:

$\frac{\sum_{i = 0}^{T / dt}{|f(i \cdot t_{\mathit{iter}}) - g(i \cdot t_{\mathit{iter}})|}}{\sum_{i = 0}^{T / dt}{f(i \cdot t_{\mathit{iter}})}}$ ,

то есть это отношение невязки к значению функции.

Вычисление плотности

В зависимости от исходных данных будем вычислять плотность одним из следующих способов.

Измерение истинного значения плотности.

В каждый момент времени определяем точное значение количества автомобилей $n$ , находящихся на интересующем нас участке дороги, и вычисляем значение плотности по формуле: $\rho = \frac{n}{L}$ .

Измерение плотности на основе данных детектора.

С периодом $t_{\mathit{d}\mathit{et}}$ считаем суммарную скорость $V_{\mathit{sum}}$ и количество автомобилей $n$ , проехавших под детектором. Тогда из определения плотности следует:

$\rho = \frac{n}{S} = \frac{n}{V_{\mathit{avr} \cdot t_{\mathit{d}\mathit{et}}}} = \frac{n}{\frac{V_{\mathit{sum}}}{n} \cdot t_{\mathit{d}\mathit{et}}} = \frac{n^2}{V_{\mathit{sum}} \cdot t_{\mathit{d}\mathit{et}}}$ .

Измерение плотности на основе данных GPS-трекера.

Можно выделить два основных способа подсчета плотности транспортного потока на основе данных GPS-трекера:

отслеживание количества попавших в интересующую нас область дороги АТС для определения плотности;
вычисление средней скорости движения АТС в выделенной нами области и применение различных функционалов для определения плотности.

Минусами первого подхода, очевидно, является тот факт, что далеко не все АТС оборудованы GPS-трекерами, поэтому вычисленное значение плотности будет пропорционально зависеть от их доли. Другая проблема заключается в том, что нам не известна эта доля оборудованных GPS-трекерами АТС, иначе можно было бы просто разделить значение плотности на процент АТС с GPS-трекерами и получить реальное значение плотности транспортного потока (при условии равномерного распространения оборудования).

Минусами второго подхода (как и первого) является возможность неравномерного распределения оборудования среди АТС и погрешность измерения. Все остальное зависит уже от метода вычисления плотности.

Здесь параллельно возникает следующая интересная задача: каким образом расположение светофоров влияет на точность определения плотности транспортного потока? Насколько важно отношение времени того, когда горит зеленый свет, ко времени работы красного света. Где лучше всего следует расположить детектор: до светофора, после или прямо в одной точке вместе с ним?

Пересчет физических параметров участников дорожного движения

Отметим некоторые особенности пересчета физических параметров объектов (светофоры, АТС, детекторы), которые участвуют в эксперименте.

С пересчетом характеристик светофора и сбором статистики детектором все относительно просто, поэтому не будем заострять внимание на этих объектах. Наибольший интерес представляют АТС, для которых необходимо заново обновлять положение, скорость и ускорение на каждой итерации симуляции со временем дискретизации $t_{\mathit{a}}$ . Все эти параметры пересчитываются исходя из физических законов:

$V_{i} = V_{i - 1} + a_{i - 1} \cdot t_{\mathit{a}}$ ,

$s_{i} = V_{i - 1} \cdot t_{\mathit{a}} + a_{i - 1} \cdot \frac{t_{\mathit{a}}^2}{2}$ ,

где $a_{i - 1}, V_{i - 1}$ — ускорение, скорость АТС на предыдущем шаге соответственно; $a_{i}, V_{i}, s_{i}$ — ускорение, скорость, пройденное расстояние АТС на текущем шаге соответственно.

Особенность описанной выше конфигурации в том, что дорога является окружностью, поэтому положение АТС пересчитывается следующим образом:

$\beta_{i} = \frac{s_{i}}{R}$ ,

$x_{i} = C_{x} + R \cdot \cos{(\alpha_{i - 1} + \beta_{i})}$ ,

$y_{i} = C_{y} + R \cdot \sin{(\alpha_{i - 1} + \beta_{i})}$ ,

где $C_{x}, C_{y}$ — абсцисса и ордината центра окружности, $\alpha_{i - 1}$ — угол положения АТС в предыдущий момент времени, $\beta_{i}$ — текущий угол смещения автомобиля за время $t_{\mathit{a}}$ .

Самый изменчивый параметр АТС — ускорение $a$ , через него уже выражаются все остальные параметры. Будем изменять ускорение по следующим правилам:

пока скорость АТС не достигла некоторого максимума $V_{max}$ , ускорение будет иметь значение $a_1$ , иначе считаем ускорение равным 0;
если впереди АТС на расстоянии $L_v$ возникает какое-то препятствие в виде, например, светофора и или другого АТС, то ускорение пересчитывается согласно модели "следования за лидером".

Все параметры подбираются опытным путем.

Модель следования за лидером

Принцип простейшей модели следования за лидером в следующем: ускорение $n$ -го АТС прямо пропорционально разности скоростей $(n + 1)$ -го АТС с коэффициентом пропорциональности обратно пропорциональным расстоянию до впереди идущего АТС. То есть:

$a_n(t + \tau)=\alpha \frac{v_{n + 1}(t) - v_{n}(t)}{s_{n + 1}(t) - s_{n}(t)}, \alpha > 0$ ,

где $\alpha$ — коэффициент чувствительности, характеризующий скорость реакции водителя.

Данная модель была предложена в 1959 году сотрудниками компании Дженерал Моторс.

Измерение плотности на основе данных GPS-трекера

Модели, которые использовались для тестирования:

1) Модель Танака.

$\rho(v)=\frac{1}{d(v)},$

$d(v)= L+ c_1 v+ c_2 v^2,$

где $d(v)$ – среднее (безопасное) расстояние между АТС, $L$ – средняя длина АТС, $c_1$ – время, характеризующее реакцию водителя, $c_2$ - коэффициент пропорциональности тормозному пути. При нормальных условиях (сухой асфальт): $L=4.5, c_1=0.504, c_2=0.0285$ .

2) Модель Гриндшилдса.

$\rho= \rho_{max} (1- \frac{v}{v_{max}} ),$

где $\rho_{max}$ - максимальная плотность потока (при отсутствии движения), $v_{max}$ - максимальная скорость движения АТС (при пустой дороге).

3) Модель Гринберга.

$\rho= \rho_{max} e^{-\frac{v}{c}},$

где C – неотрицательная константа с размерностью скорости.

4) Модель Гриндшилдса-Гринберга.

$\rho= \rho_{max}(1- \frac{v}{v_{max}} )^{\frac{2}{n+1}},\:n \leq 0,$

5) Модель Гриндшилдса-Гринберга (другой вид формулы).

$\rho= \rho_{max} (1 - (n+1) \frac{v}{c} \rho_{max}^{-(n+1)/2})^{\frac{2}{n+1}},\:n \neq -1,\:n \neq 1$

где $\rho_{max}$ - максимальная плотность потока (при отсутствии движения), $v_{max}$ - максимальная скорость движения АТС (при пустой дороге), C – неотрицательная константа с размерностью скорости.

Вычислительный эксперимент

Значения параметров

Для расчетов будем использовать параметры:

Параметр	Значение
Радиус круга $R$	1000 м
Максимальная скорость $v_{max}$	16.7 м/с
Максимальная плотность $\rho_{max}$	150 шт/км
Количество итераций	300000
Период дискретизации $t_{iter}$	0.01 с
Период обновления положения АТС $t_{a}$	60.0 с
Период обновления статистики детектора $t_{d et}$	60.0 с
Время горения зеленого света $t_{green}$	20.0 с
Время горения красного света $t_{red}$	60.0 с
Длина участка дороги $L$ для измерения плотности	100.0 м
Количество АТС $n$	30 шт.

Конфигурация эксперимента:

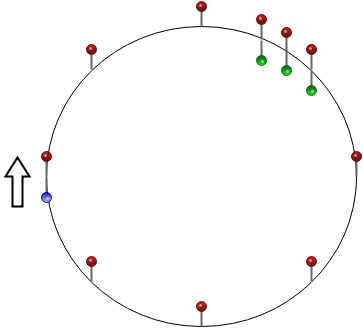
Начальная конфигурация: стрелка - направление движения, красный маркер - положения детекторов, зеленый маркер - положения светофоров (в каждом эксперименте участвует только один светофор), синий - начальное положение АТС

Результат

1. Модель №1:

Тип модели	Суммарная ошибка	Лучшие параметры
Модель Танака	17349	-

Заключение

Исходные коды программ можно найти здесь:

Моделирование движения: https://github.com/greexon/TrafficSim.
Визуализация движения: https://github.com/greexon/TrafficSimVisualizer.

Литература

Гасников А. В. Введение в математическое моделирование транспортных потоков. Москва, МФТИ, 2010.
Семенов В. В. Математическое моделирование динамики транспортных потоков мегаполиса.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9F%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%BF%D0%BB%D0%BE%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B8_%D1%82%D1%80%D0%B0%D0%BD%D1%81%D0%BF%D0%BE%D1%80%D1%82%D0%BD%D0%BE%D0%B3%D0%BE_%D0%BF%D0%BE%D1%82%D0%BE%D0%BA%D0%B0»

Категории: Анализ данных о транспортных потоках | Имитационное моделирование