Вычисление второй производной по одной переменной

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Содержание

1 Введение
- 1.1 Постановка математической задачи
2 Изложение метода
3 Числовые примеры
4 Рекомендации программисту
5 Заключение
6 Ссылки
7 Список литературы

Введение

Постановка математической задачи

Рассмотрим задачу вычисления второй производной $\frac{d^2}{d x^2}$ функции $y(x)$ . Если задачу точно решить либо не удаётся, либо слишком сложно, то приходится использовать методы численного дифференцирования.

В данном отчёте теоретически обосновываются приближенные формулы для вычисления производной:

( 1 )

$y''(x)=(y(x+h)-2y(x)+y(x-h))/h^2+O(h^2)$ .

( 2 )

$y''(x)=(-y(x+2h)+16y(x+h)-30y(x)+16y(x-h)-y(x-2h))/(12h^2)+O(h^4)$

Эти формулы можно использовать и для вычисления частной производной функции многих переменных.

После этого приводятся оценки ошибок формул (1) и (2), а также рассматривается вопрос о выборе оптимального шага $h$ .

Изложение метода

Определения

Пусть в некоторой окрестности точки $x_0 \in \mathbb{R}$ определена функция $y: U(x_0) \subset \mathbb{R} \to \mathbb{R}$ . Производной функции $y(x)$ в точке $x_0$ называется предел, если он существует,

$y'(x_0)=\lim_{x\to x_0} \frac{y(x)-y(x_0)}{x-x_0}$ .

Второй производной функции $y(x)$ в точке $x_0$ называется производная функции $y'(x)$ в точке $x_0$ . Аналогично определяются производные и более высоких порядков.

Полиномиальные формулы

При численном дифференцировании функцию $y(x)$ аппроксимируют легко вычисляемой функцией $\varphi(x)$ и приближенно полагают $y^{(k)}(x)\approx\varphi^{(k)}(x)$ . При этом можно использовать различные способы аппроксимации. Рассмотрим простейший случай - аппроксимацию интерполяционным многочленом Ньютона.

Пусть задана сетка $x_0<x_1<\dots<x_N. y(x)$ - исследуемая функция. Введем обозначение $\xi_i=x-x_i$ и введем понятие разделенные разности $y(x_0,x_1,\dots,x_k)$ , определяемые следующим образом:

$y(x_i,x_j)=\frac{y(x_i) - y(x_j)}{x_i - x_j}$ ,

$y(x_i,x_j,x_k) = \frac{y(x_i,x_j)-y(x_j,x_k)}{x_i-x_k}$ и т.д.

Можно доказать, что

$y(x_0,x_1,\dots,x_k) = \sum_{p=0}^{k}y_p \prod_{i=0, i\neq p}^k {(x_p-x_i)}^{-1}$ .

Запишем интерполяционный многочлен Ньютона и продифференцируем его почленно:

$\varphi(x)=y(x_0)+\xi_0 y(x_0,x_1)+\xi_0\xi_1 y(x_0,x_1,x_2) + \xi_0\xi_1\xi_2 y(x_0,x_1,x_2,x_3)+\dots$

$\varphi'(x)=y(x_0,x_1)+(\xi_0+\xi_1) y(x_0,x_1,x_2) + (\xi_0\xi_1+\xi_0\xi_2 +\xi_1\xi_2) y(x_0,x_1,x_2,x_3)+\dots$

$\varphi''(x)=2 y(x_0,x_1,x_2) + 2(\xi_0+\xi_1 +\xi_2) y(x_0,x_1,x_2,x_3)+\dots$

Общая формула примет следующий вид:

( 3 )

$\varphi^{(k)}(x)=k!\left[ y(x_0,x_1,\dots,x_k) + \left( \sum_{i=0}^k \xi_i \right) y(x_0,x_1,\dots,x_{k+1}) + \left( \sum_{i>j\geq 0}^{i=k+1}\xi_i\xi_j\right)y(x_0,x_1,\dots,x_{k+2}) + \left( \sum_{i>j>l\geq 0}^{i=k+2}\xi_i\xi_j\xi_l\right)y(x_0,x_1,\dots,x_{k+3}) +\dots\right]$

Обрывая ряд на некотором числе членов, получим приближенное выражение для соответствующей производной. Наиболее простые выражения получим, оставляя в формуле (3) только первый член:

$y'(x)\approx y(x_0,x_1) = \frac{y(x_0)-y(x_1)}{x_0-x_1}$ ,

( 4 )

$\frac{1}{2}y''(x)\approx y(x_0,x_1,x_2) = \frac{1}{x_0-x_2}\left( \frac{y_0-y_1}{x_0-x_1}- \frac{y_1-y_2}{x_1-x_2}\right)$ ,

$\frac{1}{k!} y^{(k)}(x) \approx y(x_0,x_1,\dots,x_k) = \sum_{p=0}^{k}y_p \prod_{i=0, i\neq p}^k {(x_p-x_i)}^{-1}$

Исследование точности полученных выражений при численных расчётах удобно делать при помощи апостериорной оценки, по скорости убывания членов ряда (3). Если шаг сетки достаточно мал, то погрешность близка к первому отброшенному члену. Пусть мы используем узлы $x_i, i=1\dots n$ . Тогда первый отброшенный член содержит разделенную разность $y(x_0,x_1,\dots,x_{n+1})$ , которая согласно (4) примерно равна $y^{(n+1)}(x)/(n+1)!$ . Перед ней стоит сумма произведений различных множителей $\xi_i$ ; каждое произведение содержит $n+1-k$ множителей, а вся сумма состоит из $C_{n+1}^k$ слагаемых. Отсюда следует оценка погрешности формулы (3) с $n+1$ узлами:

(5)

$R_n^{(k)}\leq\frac{M_{n+1}}{(n+1-k)!}\max_i {|\xi_i|}^{n+1-k},\; M_{n+1}=\max{|y^{(n+1)}|}$

В частности, если сетка равномерная, то $M_{n+1}=\max{|\xi_i|}\leq nh$ , откуда

(6)

$R_n^{(k)}<M_{n+1} {\left( \frac{en}{n+1-k}h \right)}^{n+1-k}=O(h^{n+1-k})$ .

Стоит заметить, что строгое априорное исследование погрешности формулы (3), аналогичное выводу остаточного члена многочлена Ньютона в форме Коши, для произвольного расположения узлов приводит к той же оценке (5).

Таким образом, порядок точности формулы (3) по отношению к шагу сетки равен числу оставленных в ней членов, или, что то же самое, он равен числу узлов интерполяции минус порядок производной. Поэтому минимальное число узлов, необходимое для вычисления $k$ -й производной, равно $k+1$ ; оно приводит к формулам (4) и обеспечивает первый порядок точности. Эти выводы соответствуют общему принципу: при почленном дифференцировании ряда скорость его сходимости уменьшается.

Простейшие формулы (случай равномерной сетки)

Рассмотрим равномерную сетку $x_0<x_1<\dots<x_N,\; x_{i+1}-x_i=h=const,\; y_i=y(x_i).$ При этом вид формул (3) заметно упрощается, а точность нередко повышается.

Рассмотрим сначала причину повышения точности. Остаточный член общей формулы (3) - это многочлен $\sum\prod(x-x_i)$ степени $n+1-k$ относительно $x$ . Если $x$ равен корню этого многочлена, то главный остаточный член обращается в нуль, то есть в этой точке формула имеет порядок точности на еденицу больше, чем согласно оценке (6). Эти точки повышенной точности будем обозначать $x_k^{(p)}$ , где $k$ - порядок производной, а $p=n+1-k$ - число оставленных в формуле (3) членов. Очевидно, $p$ -членная формула имеет p точек повышенной точности.

У одночленной формулы (4) для $k$ -й производной точка повышенной точности на произвольной сетке определяется учловием $\sum \xi_i=\sum(x-x_i)=0$ , что дает

(7)

$x_k^{(1)}=(x_0+x_1+\dots+x_k)/(k+1)$ ;

в этой точке одночленная формула имеет погрешность $O(h^2)$ вместо обычной $O(h)$ . Для двучленной формулы задача нахождения точек повышенной точности приводит к квадратному уравнению, корни которого действительны, но формула для их нахождения громоздка. Если $p>2$ , то найти точки повышенной точности очень сложно, за исключением одного частного случая, который мы сейчас и рассмотрим.

Утверждение. Пусть $p$ нечетно, а узлы в формуле (4) выбраны так, что они расположены симметрично относительно точки $x$ ; тогда $x$ является одной из точек повышенной точности $x_k^{(p)}$ .

На произвольной сетке условие симметрии реализуется только в исключительных случаях. Но если сетка равномерна, то каждый ее узел симметрично окружен соседними узлами. Это позволяется составить несложные формулы хорошей точности для вычисления производных в узлах сетки.

Например, возьмем три соседний узла $x_0$ , $x_1$ и $x_2$ . и вычислим первую и вторую производную в среднем узле. Выражая в одночленных формулах (4) разделенные разности через узловые значения функции, легко получим:

$y'(x_1)=(y_2-y_0)/2h+O(h_2)$ ,

(8)

$y''(x_1)=(y_2-2y_1+y_0)/h^2+O(h^2)$ .

Аналогично можно вывести формулы более высокого порядка или для более выслких производных. Например, формула для второй производной в центральной точке по пяти узлам:

(9)

$y''(x_2)=(-y_4+16y_3-30y_2+16y_1-y_0)/(12h^2)+O(h^4)$

Заметим, что формулы (8) и (9) написаны для случая равномерной сетки; применение их на неравномерной сетке приведет к грубой ошибке. Также формулы (8)и (9) совпадают с формулами (1) и (2).

На равномерной сетке для априоной оценки точности формул часто применяют способ разложения по формуле Тейлора-Макрорена. Предположим, например, что функция $y(x)$ имеет непрерыную четвертую производную, и выразим значения функции в узлах $x_{i\pm 1}$ через значения функции и ее производных в центре симметрии узлов (в данном случае этим центром является узел $x_i$ ):

$y(x_{i\pm 1})=y(x_i \pm h)= y_i \pm h y_i'+\frac{1}{2}h^2 y_i'' \pm \frac{1}{6}h^3 y_i''' + \frac{1}{24}h^4 y^{(4)}(\eta_\pm)$ ,

где $\eta_{+}$ - некая точка интервала $(x_i, x_{i+1})$ , а $\eta_{-}$ - некоторая точка итервала $(x_{i-1},x_i)$ . Подставляя эти разложения во вторую разность, стоящую в правой части формулы (8) для второй производной имеем:

$\frac{1}{h^2}(y_{i+1}-2y_i+y_{i-1})=y_i''+\frac{h^2}{24}[y^{(4)}(\eta_{+})+y^{(4)}(\eta_{-})]= y_i'' +O(h^2)$ .

Это подтверждает ранее сделанную оценку и уточняет величину остаточного члена, который оказался равен $h^2y^{(4)}(\eta)/12$ . Такой способ получения остаточного члена проще, чем непосредственное вычисление по формуле (3).

Выбор оптимального шага (регуляризация метода)

Рис.1

При численном дифференцированиии приходится вычитать друг из друга близкие значения функций. Это приводит к уничтожению первых значащих цифр, то есть к потере части достоверных знаков чила. Если значения функции известны с малой точностью, то встает вопрос - останется ли в ответе хотя один достоверный знак?

Для ответа на этот вопрос исследуем ошибки при численном дифференцировании. При интерполировании обобщенным многочленом производная $k$ -го порядка определяется согласно (4), (5) формулой типа

$y^{(k)}(x)=h^{-k}\sum_q C_q(x)y(x_q) +R_k(x).\; C_q(x)=O(1)$ .

Если формула имеет порядок точности $p$ , то, значит, ее остаточный член равен $R_k(x)\approx C(x)h^p$ . Этот остаточный член определяет погрешность метода, и он неограниченно убывает при $h\to 0$ . Его зависимость от шага изображена на рис.1 жирной линией.

Но есть еще неустарнимая погрешность, связанная с погрешностью функции $\delta y(x)$ . Поскольку точный вид этой погрешности неизвестен, можно оценить только мажоранту неустранимой погрешности $r_k=\delta*h^{-k}\sum_q|C_q|$ ; она неограниченно возрастает при $h \to 0$ (тонкая линия на рис.1). Фактически же неустранимая погрешность будет нерегулярно зависеть от величины шага, беспорядочно осцилируя в границах, определяемых мажорантой (точки на рис.1).

Пока шаг достаточно велик, при его убывании неустранимая погрешность мала по сравнению с погрешностью метода; поэтому полная погрешность убывает. При дальнейшем уменьшении шага неустранимая погрешность становится заметной, что проявляется в не вполне регулярной зависимости результатов вычислений от величины шага. Наконец, при достаточно малом шаге неустранимая погрешность становится преобладающей, и при дальнейшем уменьшении шага результат вычислений становится все меньше достоверным.

Полная погрешность мажорируется суммой $R_k+r_k$ (штриховая кривая на рис.1). Оптимальным будет шаг, соответсвующий этой кривой. Нетрудно подсчитать, что

(10)

$h_0(\delta)={\left( \frac{k\delta \sum|C_q|}{pC} \right)}^{\frac{1}{p+k}}=O(\delta^{\frac{1}{p+k}})$ .

$\min(R_k+r_k)=Ch_0^p \left( 1+\frac{p}{k} \right) =O\left(\delta^{\frac{p}{p+k}} \right)$ .

Меньший шаг невыгоден, а меньшая погрешность, вообще говоря, недостижима (хотя отдельные вычисления случайно окажутся более точными, но мы не сможем этого узнать). Эта минимальная ошибка тем менее, чем меньше погрешность входных данных и порядок вычисляемой производной и чем выше порядок точности формулы.

Очевидно, при $\delta y(x)\to 0$ можно получить сколь угодно высокую точность результата, если шаг стремится к нулю, будучи всегда не менее $h_0(\delta)$ . Но если допустить $h<h_0(\delta)$ , то результат предельного перехода может быть неправильным.

Эта тонкость связана с некорректностью задачи дифференцирования. Рассмотрим погрешность входных данных вида $\delta y(x)= m^{-1}\sin (m^2 x)$ . Она приводит к погрешности первой производной $\delta y'(x) = m \cos (m^2 x)$ . При $m \to \infty$ погрешность функции неограниченно убывает, а погрешность производной в той же норме неограниченно растет. Значит, нет непрерывной зависимости производной от функции, то есть дифференцирование некорректно. Особенно сильно это сказывается при нахождении производных высокого порядка.

Изложенный выше способ определения оптимального шага и запрещение вести расчет шагом меньше оптимального есть некоторый способ регуляризации дифференцирования, так называемая регуляризация по шагу.

Стоит заметить, что с ростом $p$ , количества узлов в сетке для вычисления производных, константы $C_q$ и $C$ в формулах (10) повышаются, поэтому увеличение $p$ разумно лишь в определенных пределах.

Числовые примеры

Далее приведены графики зависимости ошибки вычисления от шага:

	$\frac{d^2}{dx^2}e_x\|_{x=0}$	$\frac{d^2}{dx^2}\sin x\|_{x=\frac{\pi}{2}}$	$\frac{d^2}{dx^2} x^4\|_{x=1}$
Метод (1)	Рис.1	Рис.1	Рис.1
Метод (2)	Рис.1	Рис.1	Рис.1

Вычисления проводились в стандартном типе double (позволяет хранить 15 значащих десятичных цифр) языка C++.

Видно, что при слишком малом шаге полученные значения неадекватны.

Оба метода дают хорошую точность, не превосходящую теоретические оценки.

Сравнивая работу двух метотов вычисления производной, можно заметить, что второй из них получает ответ с большей точностью при меньшем шаге. Это соответсвует теоретическим выкладкам.

Заключение

В данном отчете получены теоретически и проверены практически два метода вычисления второй производной по одной переменной ((1) и (2) ). И теоретические выкладки, и эксперименты показывают, что вопрос выбора шага - очень важный. Для его разрешения можно взять оптимальный шаг (10), совпадающий с шагами показавшими наилучшие результаты при экспериментах.

Экспериментально подтверждено, что оба метода дают неплохие результаты и могут быть использованы при практическом вычислении второй производной по одной переменной.

Ссылки

Список литературы

А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. Численные методы. Лаборатория Базовых Знаний, 2003.
Н.Н.Калиткин. Численные методы. Москва «Наука», 1978.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%92%D1%8B%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B2%D1%82%D0%BE%D1%80%D0%BE%D0%B9_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D0%B9_%D0%BF%D0%BE_%D0%BE%D0%B4%D0%BD%D0%BE%D0%B9_%D0%BF%D0%B5%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%BD%D0%BE%D0%B9»

Категории: Численное дифференцирование | Учебные задачи

@@ Строка 1: / Строка 1: @@
 == Введение ==
 === Постановка математической задачи ===
-Допустим, что в некоторой точке <tex>x</tex> у функции <tex>y(x)</tex> существует производная 2-го порядка <tex>y''(x)</tex>, которую точно вычислить либо не удается, либо слишком сложно. В этом случае для приближенного нахождения производной функции требуется использовать методы численного дифференцирования.
+Рассмотрим задачу вычисления второй производной <tex>\frac{d^2}{d x^2}</tex> функции <tex>y(x)</tex>.
+Если задачу точно решить либо не удаётся, либо слишком сложно, то приходится использовать методы численного дифференцирования.
+В данном отчёте теоретически обосновываются приближенные формулы для вычисления производной:
+{{ eqno | 1 }}
+::<tex>y''(x)=(y(x+h)-2y(x)+y(x-h))/h^2+O(h^2)</tex>.
+{{ eqno | 2 }}
+::<tex>y''(x)=(-y(x+2h)+16y(x+h)-30y(x)+16y(x-h)-y(x-2h))/(12h^2)+O(h^4)</tex>
+Эти формулы можно использовать и для вычисления частной производной функции многих переменных.
+После этого приводятся оценки ошибок формул {{eqref|1}} и {{eqref|2}}, а также рассматривается вопрос о выборе оптимального шага <tex>h</tex>.
 == Изложение метода ==
-При численном дифференцировании функцию <tex>y(x)</tex> аппроксимируют легко вычисляемой функцией <tex>\varphi(x)</tex>  и приближенно полагают <tex>y^{(k)}(x)\approx\varphi^{(k)}(x)</tex>. При этом можно использовать различные способы аппроксимации. Рассмотрим простейший случай - аппроксимацию интерполяционным многочленом Ньютона. Вводя обозначение <tex>\xi_i=x-x_i</tex>, запишем это многочлен и продифференцируем его почленно:
+=== Определения ===
+Пусть в некоторой окрестности точки <tex>x_0 \in \mathbb{R}</tex> определена функция <tex>y: U(x_0) \subset \mathbb{R} \to \mathbb{R}</tex>. Производной функции <tex>y(x)</tex> в точке <tex>x_0</tex> называется предел, если он существует,
+<tex>y'(x_0)=\lim_{x\to x_0} \frac{y(x)-y(x_0)}{x-x_0}</tex>.
+Второй производной функции <tex>y(x)</tex> в точке <tex>x_0</tex> называется производная функции <tex>y'(x)</tex> в точке <tex>x_0</tex>. Аналогично определяются производные и более высоких порядков.
+=== Полиномиальные формулы ===
+При численном дифференцировании функцию <tex>y(x)</tex> аппроксимируют легко вычисляемой функцией <tex>\varphi(x)</tex>  и приближенно полагают <tex>y^{(k)}(x)\approx\varphi^{(k)}(x)</tex>. При этом можно использовать различные способы аппроксимации. Рассмотрим простейший случай - аппроксимацию интерполяционным многочленом Ньютона.
+Пусть задана сетка <tex>x_0<x_1<\dots<x_N. y(x)</tex> - исследуемая функция. Введем обозначение <tex>\xi_i=x-x_i</tex> и введем понятие разделенные разности <tex>y(x_0,x_1,\dots,x_k)</tex>, определяемые следующим образом:
+::<tex>y(x_i,x_j)=\frac{y(x_i) - y(x_j)}{x_i - x_j}</tex>,
+::<tex>y(x_i,x_j,x_k) = \frac{y(x_i,x_j)-y(x_j,x_k)}{x_i-x_k}</tex> и т.д.
+Можно доказать, что
+::<tex>y(x_0,x_1,\dots,x_k) = \sum_{p=0}^{k}y_p \prod_{i=0, i\neq p}^k {(x_p-x_i)}^{-1}</tex>.
+Запишем интерполяционный многочлен Ньютона и продифференцируем его почленно:
 ::<tex>\varphi(x)=y(x_0)+\xi_0 y(x_0,x_1)+\xi_0\xi_1 y(x_0,x_1,x_2) + \xi_0\xi_1\xi_2  y(x_0,x_1,x_2,x_3)+\dots</tex>
@@ Строка 13: / Строка 45: @@
 Общая формула примет следующий вид:
-{{ eqno | 1 }}
+{{ eqno | 3 }}
 ::<tex> \varphi^{(k)}(x)=k!\left[ y(x_0,x_1,\dots,x_k) + \left( \sum_{i=0}^k \xi_i \right) y(x_0,x_1,\dots,x_{k+1}) + \left( \sum_{i>j\geq 0}^{i=k+1}\xi_i\xi_j\right)y(x_0,x_1,\dots,x_{k+2})   + \left( \sum_{i>j>l\geq 0}^{i=k+2}\xi_i\xi_j\xi_l\right)y(x_0,x_1,\dots,x_{k+3}) +\dots\right] </tex>
-Обрывая ряд на некотором числе членов, получим приближенное выражение для соответсвующей производной. Наиболее простые выражения получим, оставляя в формуле {{eqref|1}} только первый член:
+Обрывая ряд на некотором числе членов, получим приближенное выражение для соответствующей производной. Наиболее простые выражения получим, оставляя в формуле {{eqref|3}} только первый член:
 ::<tex>y'(x)\approx y(x_0,x_1) = \frac{y(x_0)-y(x_1)}{x_0-x_1}</tex>,
-{{ eqno | 2 }}
+{{ eqno | 4 }}
 ::<tex>\frac{1}{2}y''(x)\approx y(x_0,x_1,x_2) = \frac{1}{x_0-x_2}\left( \frac{y_0-y_1}{x_0-x_1}- \frac{y_1-y_2}{x_1-x_2}\right)</tex>,
 ::<tex>\frac{1}{k!} y^{(k)}(x) \approx y(x_0,x_1,\dots,x_k) = \sum_{p=0}^{k}y_p \prod_{i=0, i\neq p}^k {(x_p-x_i)}^{-1}</tex>
-== Числовой пример ==
+Исследование точности полученных выражений при численных расчётах удобно делать  при помощи апостериорной оценки, по скорости убывания членов ряда {{eqref|3}}. Если шаг сетки достаточно мал, то погрешность близка к первому  отброшенному члену. Пусть мы используем узлы <tex>x_i, i=1\dots n</tex>. Тогда  первый отброшенный член содержит разделенную разность <tex>y(x_0,x_1,\dots,x_{n+1})</tex>, которая согласно {{eqref|4}} примерно равна <tex>y^{(n+1)}(x)/(n+1)!</tex>. Перед ней стоит сумма произведений различных множителей <tex>\xi_i </tex>; каждое произведение содержит <tex>n+1-k</tex> множителей, а вся сумма состоит из <tex>C_{n+1}^k</tex> слагаемых. Отсюда следует оценка погрешности формулы {{eqref|3}} с <tex> n+1 </tex> узлами:
+{{eqno|5}}
+::<tex>R_n^{(k)}\leq\frac{M_{n+1}}{(n+1-k)!}\max_i {|\xi_i|}^{n+1-k},\; M_{n+1}=\max{|y^{(n+1)}|}</tex>
+В частности, если сетка равномерная, то <tex>M_{n+1}=\max{|\xi_i|}\leq nh</tex>, откуда
+{{eqno|6}}
+::<tex>R_n^{(k)}<M_{n+1} {\left( \frac{en}{n+1-k}h \right)}^{n+1-k}=O(h^{n+1-k}) </tex>.
+Стоит заметить, что строгое априорное исследование погрешности формулы {{eqref|3}}, аналогичное выводу остаточного члена многочлена Ньютона в форме Коши, для произвольного расположения узлов приводит к той же оценке {{eqref|5}}.
+Таким образом, порядок точности формулы {{eqref|3}} по отношению к шагу сетки равен числу оставленных в ней членов, или, что то же самое, он равен числу узлов интерполяции минус порядок производной. Поэтому минимальное число узлов, необходимое для вычисления <tex>k</tex>-й производной, равно <tex>k+1</tex>; оно приводит к формулам {{eqref|4}} и обеспечивает первый порядок точности. Эти выводы соответствуют общему принципу: при почленном дифференцировании ряда скорость его сходимости уменьшается.
+=== Простейшие формулы (случай равномерной сетки)===
+Рассмотрим равномерную сетку <tex>x_0<x_1<\dots<x_N,\; x_{i+1}-x_i=h=const,\; y_i=y(x_i). </tex>
+При этом вид формул {{eqref|3}} заметно упрощается, а точность нередко повышается.
+Рассмотрим сначала причину повышения точности. Остаточный член общей формулы {{eqref|3}} - это многочлен <tex>\sum\prod(x-x_i)</tex> степени <tex>n+1-k</tex> относительно <tex>x</tex>. Если <tex>x</tex> равен корню этого многочлена, то главный остаточный член обращается в нуль, то есть в этой точке формула имеет порядок точности на еденицу больше, чем согласно оценке {{eqref|6}}. Эти точки повышенной точности будем обозначать <tex>x_k^{(p)}</tex>, где <tex>k</tex> - порядок производной, а <tex>p=n+1-k</tex> - число оставленных в формуле {{eqref|3}} членов. Очевидно, <tex>p</tex>-членная формула имеет p точек повышенной точности.
+У одночленной формулы {{eqref|4}} для <tex>k</tex>-й производной точка повышенной точности на произвольной сетке определяется учловием <tex>\sum \xi_i=\sum(x-x_i)=0</tex>, что дает
+{{eqno|7}}
+::<tex>x_k^{(1)}=(x_0+x_1+\dots+x_k)/(k+1)</tex>;
+в этой  точке одночленная формула имеет погрешность <tex>O(h^2)</tex> вместо обычной <tex>O(h)</tex>. Для двучленной формулы задача нахождения точек повышенной точности приводит к квадратному уравнению, корни которого действительны, но формула для их нахождения громоздка. Если <tex>p>2</tex>, то найти точки повышенной точности очень сложно, за исключением одного частного случая, который мы сейчас и рассмотрим.
+'''Утверждение.''' Пусть <tex>p</tex> нечетно, а узлы в формуле {{eqref|4}} выбраны так, что они расположены симметрично относительно точки <tex>x</tex>; тогда <tex>x</tex> является одной из точек повышенной точности <tex>x_k^{(p)}</tex>.
+На произвольной сетке условие симметрии реализуется только в исключительных случаях. Но если сетка равномерна, то каждый ее узел симметрично окружен соседними узлами. Это позволяется составить несложные формулы хорошей точности  для вычисления производных в узлах сетки.
+Например, возьмем три соседний узла <tex>x_0</tex>, <tex>x_1</tex> и <tex>x_2</tex>. и вычислим первую и вторую производную в среднем узле. Выражая в одночленных формулах {{eqref|4}} разделенные разности через узловые значения функции, легко получим:
+::<tex>y'(x_1)=(y_2-y_0)/2h+O(h_2)</tex>,
+{{eqno|8}}
+::<tex>y''(x_1)=(y_2-2y_1+y_0)/h^2+O(h^2)</tex>.
+Аналогично можно вывести формулы более высокого порядка или для более выслких производных. Например, формула для второй производной в центральной точке по пяти узлам:
+{{eqno|9}}
+::<tex>y''(x_2)=(-y_4+16y_3-30y_2+16y_1-y_0)/(12h^2)+O(h^4)</tex>
+Заметим, что формулы {{eqref|8}} и {{eqref|9}} написаны для случая равномерной сетки; применение их на неравномерной сетке приведет к грубой ошибке. Также формулы {{eqref|8}}и {{eqref|9}} совпадают с формулами {{eqref|1}} и {{eqref|2}}.
+На равномерной сетке для априоной оценки точности формул часто применяют  способ разложения по формуле Тейлора-Макрорена. Предположим, например, что функция <tex>y(x)</tex>  имеет непрерыную четвертую производную, и выразим значения функции в узлах <tex>x_{i\pm 1}</tex>  через значения функции и ее производных в центре симметрии узлов (в данном случае этим центром является узел <tex>x_i</tex>):
+::<tex>y(x_{i\pm 1})=y(x_i \pm h)= y_i \pm h y_i'+\frac{1}{2}h^2 y_i'' \pm \frac{1}{6}h^3 y_i''' + \frac{1}{24}h^4 y^{(4)}(\eta_\pm)</tex>,
+где <tex>\eta_{+}</tex> - некая точка интервала <tex>(x_i, x_{i+1})</tex>, а <tex>\eta_{-}</tex> - некоторая точка итервала <tex>(x_{i-1},x_i)</tex>. Подставляя эти разложения во вторую разность, стоящую в правой части формулы {{eqref|8}} для второй производной имеем:
+::<tex>\frac{1}{h^2}(y_{i+1}-2y_i+y_{i-1})=y_i''+\frac{h^2}{24}[y^{(4)}(\eta_{+})+y^{(4)}(\eta_{-})]= y_i'' +O(h^2) </tex>.
+Это подтверждает ранее сделанную оценку и уточняет величину остаточного члена, который оказался равен <tex>h^2y^{(4)}(\eta)/12</tex>. Такой способ получения остаточного члена проще, чем непосредственное  вычисление по формуле {{eqref|3}}.
+=== Выбор оптимального шага (регуляризация метода) ===
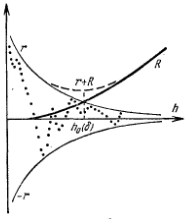
+[[Изображение:Derives.PNG|thumb|200px|Рис.1]]
+При численном дифференцированиии приходится вычитать друг из друга близкие значения функций. Это приводит к уничтожению первых значащих цифр, то есть к потере части достоверных знаков чила. Если значения функции известны с малой точностью, то встает вопрос - останется ли в ответе хотя один достоверный знак?
+Для ответа на этот вопрос исследуем ошибки при численном дифференцировании. При интерполировании обобщенным многочленом производная <tex>k</tex>-го порядка определяется согласно {{eqref|4}}, {{eqref|5}} формулой типа
+::<tex>y^{(k)}(x)=h^{-k}\sum_q C_q(x)y(x_q) +R_k(x).\; C_q(x)=O(1)</tex>.
+Если формула имеет порядок точности <tex>p</tex>, то, значит, ее остаточный член равен <tex>R_k(x)\approx C(x)h^p</tex>. Этот остаточный член определяет погрешность метода, и он неограниченно убывает при <tex>h\to 0</tex>. Его зависимость от шага изображена на рис.1 жирной линией.
+Но есть еще неустарнимая погрешность, связанная с погрешностью функции <tex>\delta y(x)</tex>. Поскольку точный вид этой погрешности неизвестен, можно оценить только мажоранту неустранимой погрешности <tex>r_k=\delta*h^{-k}\sum_q|C_q|</tex>; она неограниченно возрастает при <tex>h \to 0</tex> (тонкая линия на рис.1). Фактически же неустранимая погрешность будет нерегулярно зависеть от величины шага, беспорядочно осцилируя в границах, определяемых мажорантой (точки на рис.1).
+Пока шаг достаточно велик, при его убывании неустранимая погрешность мала по сравнению с погрешностью метода; поэтому полная погрешность убывает. При дальнейшем уменьшении шага неустранимая погрешность становится заметной, что проявляется в не вполне регулярной зависимости результатов вычислений от величины шага. Наконец, при достаточно малом шаге неустранимая погрешность становится преобладающей, и при дальнейшем уменьшении шага результат вычислений становится все меньше достоверным.
+Полная погрешность мажорируется суммой <tex>R_k+r_k</tex> (штриховая кривая на рис.1). Оптимальным будет шаг, соответсвующий этой кривой. Нетрудно подсчитать, что
+{{eqno|10}}
+::<tex>h_0(\delta)={\left( \frac{k\delta \sum|C_q|}{pC} \right)}^{\frac{1}{p+k}}=O(\delta^{\frac{1}{p+k}})</tex>.
+::<tex>\min(R_k+r_k)=Ch_0^p \left( 1+\frac{p}{k} \right) =O\left(\delta^{\frac{p}{p+k}} \right) </tex>.
+Меньший шаг невыгоден, а меньшая погрешность, вообще говоря, недостижима (хотя отдельные вычисления случайно окажутся более точными, но мы не сможем этого узнать). Эта минимальная ошибка тем менее, чем меньше погрешность входных данных и порядок вычисляемой производной и чем выше порядок точности формулы.
+Очевидно, при <tex>\delta y(x)\to 0</tex> можно получить сколь угодно высокую точность результата, если шаг стремится к нулю, будучи всегда не менее <tex>h_0(\delta)</tex>. Но если допустить <tex>h<h_0(\delta)</tex>, то результат предельного перехода может быть неправильным.
+Эта тонкость связана с некорректностью задачи дифференцирования. Рассмотрим погрешность входных данных вида <tex>\delta y(x)= m^{-1}\sin (m^2 x)</tex>. Она приводит к погрешности первой производной <tex>\delta y'(x) = m \cos (m^2 x)</tex>. При <tex>m \to \infty</tex> погрешность функции неограниченно убывает, а погрешность производной в той же норме неограниченно растет. Значит, нет непрерывной зависимости производной от функции, то есть дифференцирование некорректно. Особенно сильно это сказывается при нахождении производных высокого порядка.
+Изложенный выше способ определения оптимального шага и запрещение вести расчет шагом меньше оптимального есть некоторый способ регуляризации дифференцирования, так называемая регуляризация по шагу.
+Стоит заметить, что с ростом <tex>p</tex>, количества узлов в сетке для вычисления производных, константы <tex>C_q</tex> и <tex>C</tex> в формулах {{eqref|10}} повышаются, поэтому увеличение <tex>p</tex> разумно лишь в определенных пределах.
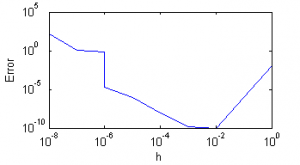
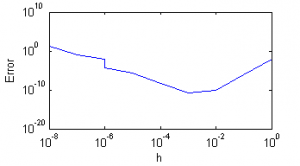
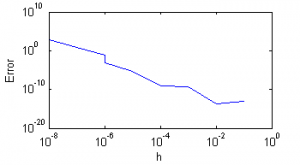
+== Числовые примеры ==
+Далее приведены графики зависимости ошибки вычисления от шага:
+{| class="standard"
+ !
+ !<tex>\frac{d^2}{dx^2}e_x|_{x=0} </tex>
+ !<tex>\frac{d^2}{dx^2}\sin x|_{x=\frac{\pi}{2}} </tex>
+ !<tex>\frac{d^2}{dx^2} x^4|_{x=1} </tex>
+ |-
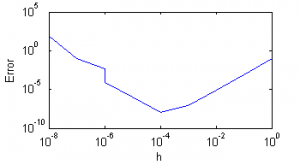
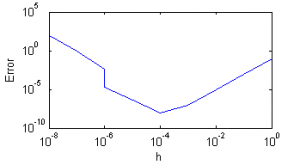
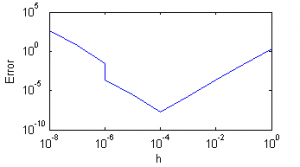
+ ! Метод {{eqref|1}}
+ |[[Изображение:Er_exp1.png|thumb|300px|Рис.1]]
+ |[[Изображение:Er_sin1.png|thumb|300px|Рис.1]]
+ |[[Изображение:Er_pol1.png|thumb|300px|Рис.1]]
+ |-
+ ! Метод {{eqref|2}}
+ |[[Изображение:Er_exp2.png|thumb|300px|Рис.1]]
+ |[[Изображение:Er_sin2.png|thumb|300px|Рис.1]]
+ |[[Изображение:Er_pol2.png|thumb|300px|Рис.1]]
+ |}
+Вычисления проводились в стандартном типе [http://en.wikipedia.org/wiki/Double_precision double] (позволяет хранить 15 значащих десятичных цифр) языка [http://ru.wikipedia.org/wiki/C%2B%2B C++].
+Видно, что при слишком малом шаге полученные значения неадекватны.
+Оба метода дают хорошую точность, не превосходящую теоретические оценки.
+Сравнивая работу двух метотов вычисления производной, можно заметить, что второй из них получает ответ с большей точностью при меньшем шаге. Это соответсвует теоретическим выкладкам.
 == Рекомендации программисту ==
+При программировании не стоит забывать, что вопрос выбора шага <tex>h</tex> очень важен.
+Исходя и экспериментов лучше всего брать шаг 0.0001 для метода {{eqref|1}}  и 0.001 - 0.01 для метода {{eqref|2}}.
 == Заключение ==
+В данном отчете получены теоретически и проверены практически два метода вычисления второй производной по одной переменной ({{eqref|1}} и {{eqref|2}} ).
+И теоретические выкладки, и эксперименты показывают, что вопрос выбора шага - очень важный. Для его разрешения можно взять оптимальный шаг {{eqref|10}}, совпадающий с шагами показавшими наилучшие результаты при экспериментах.
+Экспериментально подтверждено, что оба метода дают неплохие результаты и могут быть использованы при практическом вычислении второй производной по одной переменной.
+== Ссылки ==
+* [[Практикум ММП ВМК, 4й курс, осень 2008|Практикум ММП ВМК, 4й курс, осень 2008]]
+* [[Media:DeriveExample1.zip|  Код функций вычисления второй производной, ZIP [3Кб]]]
 == Список литературы ==
 * ''А.А.Самарский, А.В.Гулин.''&nbsp; Численные методы. Москва «Наука», 1989.
@@ Строка 33: / Строка 192: @@
 * ''Н.Н.Калиткин.''&nbsp; Численные методы. Москва «Наука», 1978.
-{{stub}}
 [[Категория:Численное дифференцирование]]
+[[Категория:Учебные задачи]]