Рациональная интерполяция
Материал из MachineLearning.
(→Введение) |
(→Пример использования) |
||
| (9 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
==Введение== | ==Введение== | ||
| - | Некоторые функции нельзя с достаточной точностью приблизить полиномами или полиномиальное приближение очень медленно сходится. В этом случае разумно обратиться к другому методу - к дробно-рациональному приближению (иногда называют просто ''рациональное''), которое | + | Некоторые функции нельзя с достаточной точностью приблизить полиномами или полиномиальное приближение очень медленно сходится. В этом случае разумно обратиться к другому методу - к дробно-рациональному приближению (иногда называют просто ''рациональное''), которое соответствует отношению двух многочленов. |
<tex>R(x)=\frac{a_0+a_1x+\dots+a_px^p}{b_0+b_1x+\dots+b_px^p}, p+q+1=n</tex> | <tex>R(x)=\frac{a_0+a_1x+\dots+a_px^p}{b_0+b_1x+\dots+b_px^p}, p+q+1=n</tex> | ||
| - | Коэффициенты <tex>a_i, b_i</tex> можно найти из совокупности соотношений <tex>R(x_j)=y_j, j=1,\ | + | Коэффициенты <tex>a_i, b_i</tex> можно найти из совокупности соотношений <tex>R(x_j)=y_j, j=1,\ldots,n,</tex> которые можно записать в виде |
| - | <tex> \sum_{j=0}^{p} a_j x_j^j-f(x_i)\sum_{j=0}^{q}b_j x_i^j=0, i=1,\ | + | <tex> \sum_{j=0}^{p} a_j x_j^j-f(x_i)\sum_{j=0}^{q}b_j x_i^j=0, i=1,\ldots, n</tex> |
| - | Таким образом | + | Таким образом получаем систему ''n'' линейных алгебраических уравнений относительно ''n+1'' неизвестных. |
| - | Функция ''R(x)'' может быть записана в явном виде в случаях, когда ''n'' | + | Функция ''R(x)'' может быть записана в явном виде в случаях, когда ''n'' нечётное и ''p=q'', и когда ''n'' чётное и ''p-q=1''. |
| + | Для этого следует вычислить обратные разделенные разности, определяемые условиями | ||
| - | = | + | <tex>f^{-}(x_k;x_l)=\frac{x_k-x_l}{f(x_k)-f(x_l)}</tex> |
| + | и рекуррентным соотношением | ||
| + | |||
| + | <tex> f^{-}(x_k;\ldots;x_l)=\frac{x_l-x_k}{f^{-}(x_{k+1};\ldots;x_l)-f^{-}(x_k;\ldots;x_{l-1})}</tex> | ||
| + | |||
| + | после чего интерполирующая рациональная функция записывается в виде цепной дроби | ||
| + | |||
| + | <tex> f^{-}(x_k;\ldots;x_n)=f(x_1)+\frac{x-x_1}{f^{-}(x_1;x_2)+\frac{x-x_2} {f^{-}(x_1;x_2;x_3)+\dots+ \frac{x-x_{n-1}}{f^{-}(x_k;\ldots;x_{n}) } } }</tex> | ||
| + | |||
| + | Дробно-рациональное интерполирование при правильном выборе узлов целесообразно использовать для функций с нерегулярным характером поведения. | ||
| + | |||
| + | ==Погрешность вычислений== | ||
==Пример использования== | ==Пример использования== | ||
| + | Выполним интерполяцию для узлов интерполяции, полученных из функции f(t)=ln(t).<br> | ||
| + | Узлы интерполяции: <br> | ||
| + | :: t:=[1., 2., 3., 4., 5.]; <br> | ||
| + | :: f(t):= [0., 0.69314718055994530942, 1.0986122886681096914, 1.3862943611198906188, 1.6094379124341003746]; <br> | ||
| + | Выполняя интерполяцию по заданным узлам, получаем: <br> | ||
| + | <tex>\Omega(t):=\frac{t-1.}{1.4426950408889634074+\frac{t-2.}{2.6470193430160504848+\frac{t-3.}{5.0781780711298101893+.72138672314187706016*t}}}</tex><br> | ||
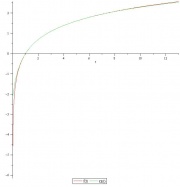
| + | Выполним построение графиков функции и выполним оценку погрешностей: | ||
| + | [[Изображение:Thiele_interpolation.jpg|thumb]] | ||
| + | Для исследования функции Ω(t) выполним экстраполяцию внутрь таблицы, взяв для определенности t=1.161.<br> | ||
| + | ln(1.161)=0.14928170271575444560<br> | ||
| + | Ω(1.161)=0.14858464422075798083<br> | ||
| + | |||
| + | Вычислим относительную погрешность для данного значения при использовании рациональной интерполяции<br> | ||
| + | δ<sub>Ω(1.161)</sub>:=0.0046913225700552061895<br> | ||
| + | |||
| + | Выполним экстраполяцию вперед таблицы, взяв для определенности t=6.103.<br> | ||
| + | δ<sub>Ω(6.103)</sub>:=0.00033164210935389932321 | ||
| + | |||
| + | ==Литературы== | ||
| + | # ''Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков.'' Численные методы. Изд-во "Лаборатория базовых знаний". 2003. | ||
| + | == См. также == | ||
| + | * [[Практикум ММП ВМК, 4й курс, осень 2008]] | ||
| - | + | [[Категория:Учебные задачи]] | |
Текущая версия
Содержание |
Введение
Некоторые функции нельзя с достаточной точностью приблизить полиномами или полиномиальное приближение очень медленно сходится. В этом случае разумно обратиться к другому методу - к дробно-рациональному приближению (иногда называют просто рациональное), которое соответствует отношению двух многочленов.
Коэффициенты можно найти из совокупности соотношений
которые можно записать в виде
Таким образом получаем систему n линейных алгебраических уравнений относительно n+1 неизвестных. Функция R(x) может быть записана в явном виде в случаях, когда n нечётное и p=q, и когда n чётное и p-q=1. Для этого следует вычислить обратные разделенные разности, определяемые условиями
и рекуррентным соотношением
после чего интерполирующая рациональная функция записывается в виде цепной дроби
Дробно-рациональное интерполирование при правильном выборе узлов целесообразно использовать для функций с нерегулярным характером поведения.
Погрешность вычислений
Пример использования
Выполним интерполяцию для узлов интерполяции, полученных из функции f(t)=ln(t).
Узлы интерполяции:
- t:=[1., 2., 3., 4., 5.];
- f(t):= [0., 0.69314718055994530942, 1.0986122886681096914, 1.3862943611198906188, 1.6094379124341003746];
- t:=[1., 2., 3., 4., 5.];
Выполняя интерполяцию по заданным узлам, получаем:
Выполним построение графиков функции и выполним оценку погрешностей:
Для исследования функции Ω(t) выполним экстраполяцию внутрь таблицы, взяв для определенности t=1.161.
ln(1.161)=0.14928170271575444560
Ω(1.161)=0.14858464422075798083
Вычислим относительную погрешность для данного значения при использовании рациональной интерполяции
δΩ(1.161):=0.0046913225700552061895
Выполним экстраполяцию вперед таблицы, взяв для определенности t=6.103.
δΩ(6.103):=0.00033164210935389932321
Литературы
- Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные методы. Изд-во "Лаборатория базовых знаний". 2003.