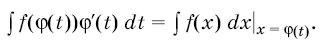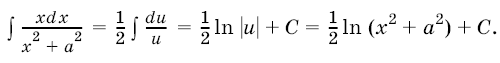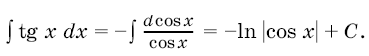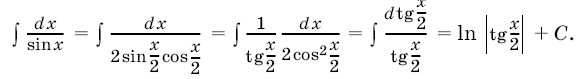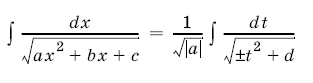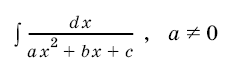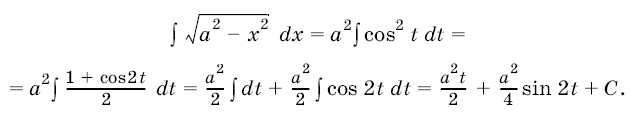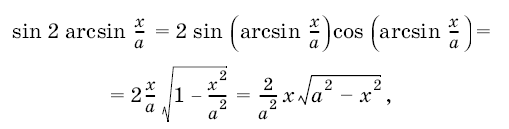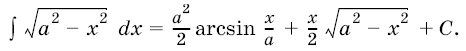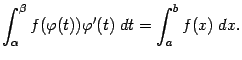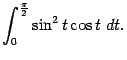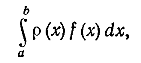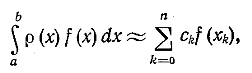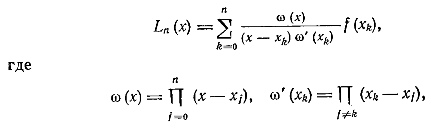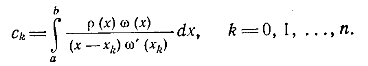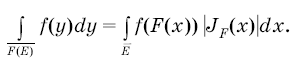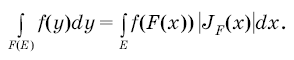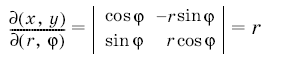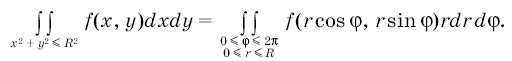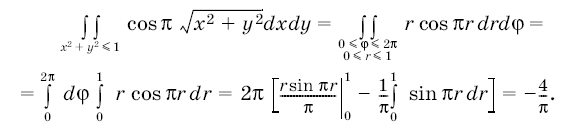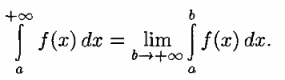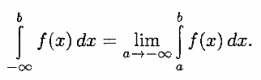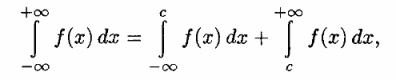Стандартизация задач с помощью замены переменных
Материал из MachineLearning.
(→Заключение) |
|||
| (10 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
== Введение == | == Введение == | ||
| - | |||
| - | + | Задача интегрирования функций значительно сложнее задачи дифференцирования. Здесь отсутствуют правила интегрирования произведения и частного двух функций, сложной и обратной функций. Имеются лишь некоторый приемы, позволяющие интегрировать отдельные классы функций. Методы замены переменных позволяют свести исходный интеграл к более простому с помощью перехода от старой переменной интегрирования к новой. | |
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
== Формула замены переменных в неопределенном интеграле == | == Формула замены переменных в неопределенном интеграле == | ||
Рассмотрим свойство неопределенного интеграла, часто оказывающееся полезным при вычислении первообразных элементарных функций. | Рассмотрим свойство неопределенного интеграла, часто оказывающееся полезным при вычислении первообразных элементарных функций. | ||
| Строка 129: | Строка 84: | ||
Заметим, что для проверки результата, полученного при вычислении неопределенного интеграла, достаточно его продифференцировать, после чего должно получиться подынтегральное выражение вычисляемого иптеграла. | Заметим, что для проверки результата, полученного при вычислении неопределенного интеграла, достаточно его продифференцировать, после чего должно получиться подынтегральное выражение вычисляемого иптеграла. | ||
| + | ==Формула замены переменных в определенном интеграле == | ||
| + | |||
| + | '''Теорема.''' | ||
| + | |||
| + | Пусть функция <tex> f(x) </tex> непрерывна на отрезке <tex> [a'; b'] </tex> , а функция <tex> \phi(t) </tex> имеет непрерывную производную <tex> \phi'(t) </tex> на отрезке <tex> [\alpha; \beta] </tex>, причём все значения <tex> x = \phi(t) </tex> при <tex> [t \in{\alpha};{\beta}] </tex> принадлежат отрезку <tex> [a'; b'] </tex>, в том числе <tex> \phi(\alpha) = a </tex> и <tex> \phi(\beta) = b </tex>. Тогда имеет место равенство | ||
| + | |||
| + | <p align = "center"> | ||
| + | [[Изображение:Img1.png]] </p> | ||
| + | |||
| + | '''Замечание.''' | ||
| + | |||
| + | Заметим, что доказанная формула, в отличие от формулы замены переменной в неопределённом интеграле, даёт нам возможность после перехода к интегралу от функции новой переменной <tex> x </tex> не возвращаться к исходному интегралу от функции переменной <tex> t </tex>. После того, как замена сделана, мы можем "забыть", как выглядел исходный интеграл, и продолжать преобразования интеграла от функции новой переменной. Именно на том, что к старой переменной возвращаться не приходится, мы и получаем экономию усилий при применении формулы замены переменной в определённом интеграле, по сравнению с тем, что получилось бы, если бы мы просто нашли первообразную и применили формулу Ньютона - Лейбница. | ||
| + | |||
| + | Обратим ваше внимание на важную особенность формулы: кроме подынтегрального выражения, при замене переменной меняются и пределы интегрирования. Действительно, в интеграле по новой переменной <tex> x </tex> должны быть указаны пределы изменения именно <tex> x </tex> (то есть <tex> a </tex> и <tex> b </tex>), в то время как в исходном интеграле по переменной <tex> t </tex> указаны пределы изменения <tex> t </tex> (то есть <tex> \alpha </tex> и <tex> \beta </tex>). | ||
| + | |||
| + | Советы о том, какая замена целесообразна для вычисления того или иного интеграла, - те же самые, что и при вычислении неопределённых интегралов, так что тут ничего нового изучать не придётся. | ||
| + | |||
| + | '''Пример.''' | ||
| + | |||
| + | Вычислим интеграл | ||
| + | |||
| + | ::[[Изображение:Img2.png]] | ||
| + | |||
| + | Для этого сделаем замену <tex> x = \phi(t) = \sin t </tex>, откуда <tex> dx = \phi'(t)dt = \cos t dt</tex>. Кроме того, при <tex> t = 0 </tex> имеем <tex> x = \sin 0 = 0 </tex>, а при <tex> t = \frac{\pi}{2} </tex> имеем <tex> x = \sin \frac{\pi}{2} = 1 </tex>. Получаем: | ||
| + | |||
| + | ::[[Изображение:Img2.png]] | ||
=== Квадратурные формулы интерполяционного типа === | === Квадратурные формулы интерполяционного типа === | ||
| + | |||
| + | Будем рассматривать формулы приближенного вычисления интегралов | ||
| + | |||
| + | ::[[Изображение:W1.png]] (3) | ||
| + | |||
| + | где <tex> p(x) > 0 </tex> — заданная интегрируемая функция (так называемая весовая функция) и <tex> f(x) </tex> — достаточно гладкая функция. Рассматриваемые далее формулы имеют вид | ||
| + | |||
| + | ::[[Изображение:W2.png]] (4) | ||
| + | |||
| + | где <tex> x \in[{a};{b}] </tex> и <tex> c_k </tex> — числа, <tex> k = 0, 1, ..., n </tex>. | ||
| + | |||
| + | Получим квадратурные формулы путем замены <tex> f(x) </tex> интерполяционным многочленом сразу на всем отрезке <tex> [a, b] </tex>. Полученные таким образом формулы называются ''квадратурными формулами интерполяционного типа''. Как правило, точность этих формул возрастает с увеличением числа узлов интерполирования. Формулы прямоугольников, трапеций и Симпсона являются частными случаями квадратурных формул интерполяционного типа, когда <tex> n = 0, 1, 2, p(x) = 1 </tex>. | ||
| + | |||
| + | Получим выражения для коэффициентов квадратурных формул интерполяционного типа. | ||
| + | Пусть на отрезке <tex> [a, b] </tex> заданы узлы интерполирования <tex> x_k, k = 0, 1, ... n </tex>. Предполагается, что среди этих узлов нет совпадающих, в остальном они могут быть расположены как угодно на <tex> [a, b] </tex>. | ||
| + | |||
| + | Заменяя в интеграле {{eqref|3}} функцию <tex> f(x) </tex> интерполяционным многочленом Лагранжа | ||
| + | |||
| + | ::[[Изображение:W3.png]] | ||
| + | |||
| + | получим приближенную формулу {{eqref|4}}, где | ||
| + | |||
| + | ::[[Изображение:W4.png]] (5) | ||
| + | |||
| + | Таким образом, формула {{eqref|4}} является квадратурной формулой интерполяционного типа тогда и только тогда, когда ее коэффициенты вычисляются по правилу {{eqref|5}}. | ||
| + | |||
== Формула замены переменных в кратном интеграле == | == Формула замены переменных в кратном интеграле == | ||
| + | |||
| + | Пусть <tex> F </tex> — непрерывно дифференцируемое взаимпо-однозпачное отображение открытого множества <tex> G \subset R_{x}^{n} </tex> в пространство <tex> R_{y}^{n} </tex> и его якобиан <tex> J_{F} </tex> не обращается в нуль на множестве <tex> G </tex>. | ||
| + | |||
| + | '''Теорема.''' | ||
| + | |||
| + | Если <tex> E </tex> — измеримое множество, содержащееся вместе со своим замыканием <tex> \bar{E} </tex> в открытом множестве <tex> G </tex>: <tex> E \subset \bar{E} \subset G </tex>, а функция <tex> f </tex> непрерывна на множестве <tex> \bar{F(E)} </tex>, то | ||
| + | |||
| + | <p align = "center"> | ||
| + | [[Изображение:A1.png]] (6) </p> | ||
| + | |||
| + | Эта формула равносильна формуле | ||
| + | |||
| + | <p align = "center"> | ||
| + | [[Изображение:A2.png]] (7) </p> | ||
| + | |||
| + | Действительно, ограниченная функция одновременно интегрируема или нет как на измеримом множестве, так и на его замыкании, причем в случае интегрируемости интегралы от функции по множеству и по его замыканию совпадают. | ||
| + | |||
| + | В нашем случае функции <tex> f(y) </tex> и [[Изображение:A3.png]] непрерывны соответственно на компактах <tex> \bar{F(E)} </tex> и <tex> \bar{E} </tex> (являющихся замыканием измеримых множеств <tex> F(E) </tex> и <tex> E </tex>), следовательно, ограничены и интегрируемы на них. | ||
| + | |||
| + | Таким образом, все входящие в формулы {{eqref|6}} и {{eqref|7}} интегралы существуют, а сами эти формулы равносильны. Эти формулы называются ''формулами замены переменных в кратном интеграле''. | ||
| + | |||
| + | Замена переменных в кратном интеграле часто существенно упрощает его исследование и вычисление. При этом в отличие от однократного интеграла нередко целью замены переменного является не упрощение подынтегральной функции, а переход к более простой области интегрирования даже ценой некоторого усложнения подынтегральной функции. | ||
| + | |||
| + | В качестве примера применения формулы замены переменных в кратном интеграле рассмотрим для двумерного интеграла случай перехода от декартовых координат к полярным. | ||
| + | |||
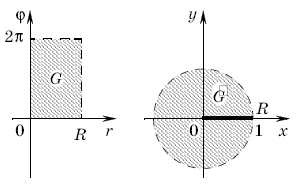
| + | Рассмотрим плоскость, на которой декартовы координаты обозначены <tex> r </tex>, <tex> \varphi </tex> и на ней открытый прямоугольник | ||
| + | |||
| + | ::[[Изображение:A4.png]] | ||
| + | |||
| + | При отображении | ||
| + | |||
| + | ::[[Изображение:A5.png]] (8) | ||
| + | |||
| + | прямоугольник <tex> G </tex> отображается на множество <tex> G </tex> плоскости с декартовыми координатами <tex> x, y </tex>, которое представляет собой круг [[Изображение:A6.png]], из которого удален радиус [[Изображение:A7.png]]. | ||
| + | |||
| + | Отображение {{eqref|8}} и его якобиан | ||
| + | |||
| + | ::[[Изображение:A8.png]] | ||
| + | |||
| + | непрерывно продолжаемы на замкнутый прямоугольник | ||
| + | |||
| + | ::[[Изображение:A9.png]] | ||
| + | |||
| + | образом которого при продолженном отображении является замкнутый круг <tex> G </tex>, на котором | ||
| + | отображение {{eqref|8}} уже не является взаимно-однозначным: взаимная однозначность нарушается на границе прямоугольника <tex> G </tex> — отрезки [[Изображение:A10.png]] при <tex> \varphi = 0 </tex> и <tex> \varphi = 2 \pi </tex> отображаются в один и тот же отрезок [[Изображение:A10.png]], <tex> y = 0 </tex>, а отрезок [[Изображение:A11.png]]и вовсе отображается в точку (0, 0). Якобиан продолженного отображения обращается в нуль при <tex> r = 0 </tex>. | ||
| + | |||
| + | <p align = "center"> | ||
| + | [[Изображение:A15.png]] </p> | ||
| + | |||
| + | Для отображения {{eqref|8}} и непрерывной на круге [[Изображение:A12.png]] функции <tex> f(x)(y) </tex> имеет место формула | ||
| + | |||
| + | ::[[Изображение:A13.png]] | ||
| + | |||
| + | Приведем конкретный пример вычисления интеграла по этой формуле: | ||
| + | |||
| + | ::[[Изображение:A14.png]] | ||
| + | |||
== Сведения об интегралах с бесконечными пределами == | == Сведения об интегралах с бесконечными пределами == | ||
| - | == | + | |
| - | + | '''Определение.''' | |
| + | |||
| + | Пусть функция <tex> f(x) </tex> непрерывна на бесконечном промежутке <tex> [a, \infty) </tex>. ''Несобственным интегралом'' от функции <tex> f(x) </tex> на промежутке <tex> [a, \infty) </tex> называется предел [[Изображение:Z1.png]] | ||
| + | и обозначается | ||
| + | |||
| + | ::[[Изображение:Z2.png]] | ||
| + | |||
| + | '''Определение.''' | ||
| + | |||
| + | Пусть функция <tex> f(x) </tex> непрерывна на бесконечном промежутке <tex> (-\infty, b) </tex>. ''Несобственным интегралом'' от функции f(x) на промежутке <tex> (-\infty, b) </tex> называется предел [[Изображение:Z3.png]] | ||
| + | и обозначается | ||
| + | |||
| + | ::[[Изображение:Z4.png]] | ||
| + | |||
| + | '''Определение.''' | ||
| + | |||
| + | Пусть функция <tex> f(x) </tex> непрерывна на всей числовой оси. Несобственный интеграл от функции <tex> f(x) </tex> на бесконечном промежутке <tex> (-\infty, +\infty) </tex> определяется равенством | ||
| + | |||
| + | ::[[Изображение:Z5.png]] | ||
| + | |||
| + | где <tex> c </tex> — любое число на оси <tex> Ox </tex>. | ||
| + | |||
| + | Из определений следует, что сходящиеся несобственные интегралы с бесконечными пределами интегрирования являются конечными пределами определенных интегралов с переменными верхним или нижним пределами при стремлении этих пределов к бесконечности. | ||
| + | |||
| + | Пусть функция <tex> f(x) </tex> непрерывна и неотрицательна на бесконечном промежутке <tex> [a, \infty) </tex>. Известно, что интеграл <tex> \int_{a}^{b} f(x) dx </tex> численно равен площади криволинейной трапеции, ограниченной снизу отрезком <tex> [a, b] </tex> оси <tex> Ox </tex>, сверху — кривой <tex> y = f(x) </tex>, слева и справа — прямыми <tex> x = a </tex> и <tex> x = b </tex>. При возрастании <tex> b </tex> прямая <tex> x = b </tex> перемещается вправо вдоль оси <tex> Ox </tex>. Если при этом интеграл <tex> \int_{a}^{+\infty} f(x) dx </tex> сходится, то его величину принимают за площадь бесконечной трапеции, ограниченной снизу осью <tex> Ox </tex>, сверху — графиком функции <tex> y = f(x) </tex>, слева — прямой <tex> x = a </tex>. | ||
| + | |||
| + | ::[[Изображение:Z6.png]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
== Литература == | == Литература == | ||
Текущая версия
Содержание |
Введение
Задача интегрирования функций значительно сложнее задачи дифференцирования. Здесь отсутствуют правила интегрирования произведения и частного двух функций, сложной и обратной функций. Имеются лишь некоторый приемы, позволяющие интегрировать отдельные классы функций. Методы замены переменных позволяют свести исходный интеграл к более простому с помощью перехода от старой переменной интегрирования к новой.
Формула замены переменных в неопределенном интеграле
Рассмотрим свойство неопределенного интеграла, часто оказывающееся полезным при вычислении первообразных элементарных функций.
Теорема.
Пусть функции и
определены соответственно на промежутках
и
, причем
. Если функция
имеет на
первообразную
и, следовательно,
а функция дифференцируема на
, то функция
имеет на
, первообразную
и
Формула (1) называется формулой интегрирования подстановкой, а именно подстановкой . Это название объясняется тем, что если формулу (2) записать в виде
то будет видно, что, для того чтобы вычислить интеграл ![]() ), можно сделать подстановку
), можно сделать подстановку , вычислить интеграл
и затем вернуться к переменной
, положив
.
Примеры.
1. Для вычисления интеграла естественно сделать подстановку
, тогда
2. Для вычисления интеграла 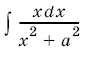 удобно применить подстановку
удобно применить подстановку
:
3. При вычислении интегралов вида ![]() полезна подстановка
полезна подстановка
:
Например,
Иногда, прежде чем применить метод интегрирования подстановкой, приходится проделать более сложные преобразования подынтегральной функции:
Отметим, что формулу (2) бывает целесообразно использовать и в обратном порядке, т.е. справа палево. Именно, иногда удобно вычисление интеграла с помощью соответствующей замены переменного
свести к вычислению интеграла
![]() (если этот интеграл в каком-то смысле «проще» исходного).
(если этот интеграл в каком-то смысле «проще» исходного).
В случае, когда функция имеет обратную
, перейдя в обеих частях формулы (2) к переменной
с помощью подстановки
и поменяв местами стороны равенства, получим
Эта формула называется обычно формулой интегрирования заменой переменной.
Для того чтобы существовала функция , обратная
, в дополнение к условиям теоремы достаточно, например, потребовать, чтобы на рассматриваемом промежутке
функция
была строго монотонной. В этом случае, существует однозначная обратная функция
.
4. Интегралы вида 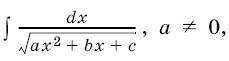 в том случае, когда подкоренное выражение неотрицательно на некотором промежутке, легко сводятся с помощью заме¬ны переменного к табличным.
в том случае, когда подкоренное выражение неотрицательно на некотором промежутке, легко сводятся с помощью заме¬ны переменного к табличным.
Действительно, замечая, что 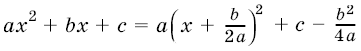 , сделаем замену переменной
, сделаем замену переменной ![]() и положим
и положим 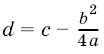 . Тогда
. Тогда 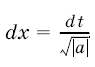 и, в силу формулы (2), получим
и, в силу формулы (2), получим
(перед стоит знак плюс, если а > 0, и знак минус, если а < 0). Интеграл, стоящий в правой части равенства, является табличным. Найдя его по соответствующим формулам и вернувшись от переменной
к переменной
, получим искомый интеграл.
Подобным же приемом вычисляются и интегралы вида
5. Интеграл ![]() можно вычислить с помощью подстановки
можно вычислить с помощью подстановки
. Имеем
, поэтому
Подставляя это выражение и замечая, что
окончательно будем иметь
Заметим, что для проверки результата, полученного при вычислении неопределенного интеграла, достаточно его продифференцировать, после чего должно получиться подынтегральное выражение вычисляемого иптеграла.
Формула замены переменных в определенном интеграле
Теорема.
Пусть функция непрерывна на отрезке
, а функция
имеет непрерывную производную
на отрезке
, причём все значения
при
принадлежат отрезку
, в том числе
и
. Тогда имеет место равенство
Замечание.
Заметим, что доказанная формула, в отличие от формулы замены переменной в неопределённом интеграле, даёт нам возможность после перехода к интегралу от функции новой переменной не возвращаться к исходному интегралу от функции переменной
. После того, как замена сделана, мы можем "забыть", как выглядел исходный интеграл, и продолжать преобразования интеграла от функции новой переменной. Именно на том, что к старой переменной возвращаться не приходится, мы и получаем экономию усилий при применении формулы замены переменной в определённом интеграле, по сравнению с тем, что получилось бы, если бы мы просто нашли первообразную и применили формулу Ньютона - Лейбница.
Обратим ваше внимание на важную особенность формулы: кроме подынтегрального выражения, при замене переменной меняются и пределы интегрирования. Действительно, в интеграле по новой переменной должны быть указаны пределы изменения именно
(то есть
и
), в то время как в исходном интеграле по переменной
указаны пределы изменения
(то есть
и
).
Советы о том, какая замена целесообразна для вычисления того или иного интеграла, - те же самые, что и при вычислении неопределённых интегралов, так что тут ничего нового изучать не придётся.
Пример.
Вычислим интеграл
Для этого сделаем замену , откуда
. Кроме того, при
имеем
, а при
имеем
. Получаем:
Квадратурные формулы интерполяционного типа
Будем рассматривать формулы приближенного вычисления интегралов
где — заданная интегрируемая функция (так называемая весовая функция) и
— достаточно гладкая функция. Рассматриваемые далее формулы имеют вид
где и
— числа,
.
Получим квадратурные формулы путем замены интерполяционным многочленом сразу на всем отрезке
. Полученные таким образом формулы называются квадратурными формулами интерполяционного типа. Как правило, точность этих формул возрастает с увеличением числа узлов интерполирования. Формулы прямоугольников, трапеций и Симпсона являются частными случаями квадратурных формул интерполяционного типа, когда
.
Получим выражения для коэффициентов квадратурных формул интерполяционного типа.
Пусть на отрезке заданы узлы интерполирования
. Предполагается, что среди этих узлов нет совпадающих, в остальном они могут быть расположены как угодно на
.
Заменяя в интеграле (3) функцию интерполяционным многочленом Лагранжа
получим приближенную формулу (4), где
Таким образом, формула (4) является квадратурной формулой интерполяционного типа тогда и только тогда, когда ее коэффициенты вычисляются по правилу (5).
Формула замены переменных в кратном интеграле
Пусть — непрерывно дифференцируемое взаимпо-однозпачное отображение открытого множества
в пространство
и его якобиан
не обращается в нуль на множестве
.
Теорема.
Если — измеримое множество, содержащееся вместе со своим замыканием
в открытом множестве
:
, а функция
непрерывна на множестве
, то
Эта формула равносильна формуле
Действительно, ограниченная функция одновременно интегрируема или нет как на измеримом множестве, так и на его замыкании, причем в случае интегрируемости интегралы от функции по множеству и по его замыканию совпадают.
В нашем случае функции и
![]() непрерывны соответственно на компактах
непрерывны соответственно на компактах и
(являющихся замыканием измеримых множеств
и
), следовательно, ограничены и интегрируемы на них.
Таким образом, все входящие в формулы (6) и (7) интегралы существуют, а сами эти формулы равносильны. Эти формулы называются формулами замены переменных в кратном интеграле.
Замена переменных в кратном интеграле часто существенно упрощает его исследование и вычисление. При этом в отличие от однократного интеграла нередко целью замены переменного является не упрощение подынтегральной функции, а переход к более простой области интегрирования даже ценой некоторого усложнения подынтегральной функции.
В качестве примера применения формулы замены переменных в кратном интеграле рассмотрим для двумерного интеграла случай перехода от декартовых координат к полярным.
Рассмотрим плоскость, на которой декартовы координаты обозначены ,
и на ней открытый прямоугольник
При отображении
прямоугольник отображается на множество
плоскости с декартовыми координатами
, которое представляет собой круг
![]() , из которого удален радиус
, из которого удален радиус ![]() .
.
Отображение (8) и его якобиан
непрерывно продолжаемы на замкнутый прямоугольник
образом которого при продолженном отображении является замкнутый круг , на котором
отображение (8) уже не является взаимно-однозначным: взаимная однозначность нарушается на границе прямоугольника
— отрезки
![]() при
при и
отображаются в один и тот же отрезок
![]() ,
, , а отрезок
![]() и вовсе отображается в точку (0, 0). Якобиан продолженного отображения обращается в нуль при
и вовсе отображается в точку (0, 0). Якобиан продолженного отображения обращается в нуль при .
Для отображения (8) и непрерывной на круге ![]() функции
функции имеет место формула
Приведем конкретный пример вычисления интеграла по этой формуле:
Сведения об интегралах с бесконечными пределами
Определение.
Пусть функция непрерывна на бесконечном промежутке
. Несобственным интегралом от функции
на промежутке
называется предел
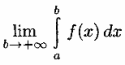 и обозначается
и обозначается
Определение.
Пусть функция непрерывна на бесконечном промежутке
. Несобственным интегралом от функции f(x) на промежутке
называется предел
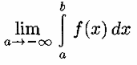 и обозначается
и обозначается
Определение.
Пусть функция непрерывна на всей числовой оси. Несобственный интеграл от функции
на бесконечном промежутке
определяется равенством
где — любое число на оси
.
Из определений следует, что сходящиеся несобственные интегралы с бесконечными пределами интегрирования являются конечными пределами определенных интегралов с переменными верхним или нижним пределами при стремлении этих пределов к бесконечности.
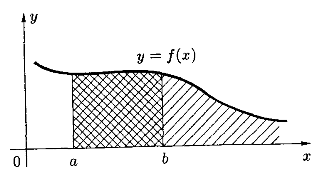
Пусть функция непрерывна и неотрицательна на бесконечном промежутке
. Известно, что интеграл
численно равен площади криволинейной трапеции, ограниченной снизу отрезком
оси
, сверху — кривой
, слева и справа — прямыми
и
. При возрастании
прямая
перемещается вправо вдоль оси
. Если при этом интеграл
сходится, то его величину принимают за площадь бесконечной трапеции, ограниченной снизу осью
, сверху — графиком функции
, слева — прямой
.
Литература
- Л.Д. Кудрявцев. Курс математического анализа в 3 томах.
- З.И. Гурова, С.Н. Каролинская, А.П. Осипова. Математический анализ. Начальный курс с примерами и задачами.
- А.А. Самарский, А.В. Гулин. Численные методы М.: Наука, 1989.
- http://de.ifmo.ru/bk_netra/page.php?index=42&layer=1&tutindex=21#2
- http://sesia5.ru/vmat/gl5/21.html