Метод простых итераций
Материал из MachineLearning.
| (7 промежуточных версий не показаны.) | |||
| Строка 18: | Строка 18: | ||
'''Следствие 1.''' Если <tex>|g'(x)| \le q < 1</tex> для <tex>x \in U_r(a)</tex>, выполнено <tex>|g(a)-a|<(1-q)r</tex>, и <tex>x_0 \in U_r(a)</tex>, тогда уравнение <tex>x = g(x)</tex> имеет единственное решение на <tex>U_r(a)</tex> и метод простой итерации сходится к решению.<br><br> | '''Следствие 1.''' Если <tex>|g'(x)| \le q < 1</tex> для <tex>x \in U_r(a)</tex>, выполнено <tex>|g(a)-a|<(1-q)r</tex>, и <tex>x_0 \in U_r(a)</tex>, тогда уравнение <tex>x = g(x)</tex> имеет единственное решение на <tex>U_r(a)</tex> и метод простой итерации сходится к решению.<br><br> | ||
'''Следствие 2.''' Если уравнение <tex>x = g(x)</tex> имеет решение <tex>x_*</tex>, <tex>g(x)</tex> непрерывно дифференцируема на <tex>U_r(x_*)</tex> и <tex>|g'(x_*)|<1</tex>. Тогда существует <tex>\eps > 0</tex> такое, что на <tex>U_{\eps}(x_*)</tex> уравнение не имеет других решений и метод простой итерации сходится к решению при <tex>x_0 \in U_{\eps}(x_*)</tex><br> | '''Следствие 2.''' Если уравнение <tex>x = g(x)</tex> имеет решение <tex>x_*</tex>, <tex>g(x)</tex> непрерывно дифференцируема на <tex>U_r(x_*)</tex> и <tex>|g'(x_*)|<1</tex>. Тогда существует <tex>\eps > 0</tex> такое, что на <tex>U_{\eps}(x_*)</tex> уравнение не имеет других решений и метод простой итерации сходится к решению при <tex>x_0 \in U_{\eps}(x_*)</tex><br> | ||
| + | ===Геометрическая интерпретация=== | ||
| + | Рассмотрим график функции <tex> y = g(x)</tex>. Это озночает, что решение уравнения <tex>f(x) = 0</tex> и <tex>x=g(x)</tex> - это точка пересечения <tex>g(x)</tex> с прямой <tex>y = x</tex>:<br> | ||
| + | <center>[[Изображение:PowerIterationMethod.jpg|300px]]</center> | ||
| + | И следующая итерация <tex>x_{x+1} = g(x_n)</tex> - это координата <tex>x</tex> пересечения горизонтальной прямой точки <tex>(x_n g(x_n))</tex> с прямой <tex>y = x</tex>.<br> | ||
| + | <center>[[Изображение:PowerIterationMethod4.jpg|300px]]</center> | ||
| + | <br> | ||
| + | Из рисунка наглядно видно требование сходимости <tex>|g'(x)|<1</tex>. Чем ближе производная <tex>g'(x)</tex> к <tex>0</tex>, тем быстрее сходится алгоритм. В зависимости от знака производной вблизи решения приближения могут строится по разному. Если <tex>g'(x)<0</tex>, то каждое следующее приближение строится с другой стороны от корня:<br> | ||
| + | <center>[[Изображение:PowerIterationMethod2.jpg|300px]]</center> | ||
==Метод релаксации== | ==Метод релаксации== | ||
Так как для сходимости метода очень важен выбор функции <tex>g(x)</tex>, ее обычно берут вида <center><tex>g(x)=x+s(x)f(x)</tex> <tex>(1)</tex>.</center> | Так как для сходимости метода очень важен выбор функции <tex>g(x)</tex>, ее обычно берут вида <center><tex>g(x)=x+s(x)f(x)</tex> <tex>(1)</tex>.</center> | ||
| Строка 85: | Строка 93: | ||
== Примеры тестирования == | == Примеры тестирования == | ||
| + | Ошибкой будем считать <tex>\eps = f(x_k)-f(x_*) = f(x_k)</tex> и проверим скорость сходимости методов относительно друг друга.<br> | ||
<tex>f(x) = -(\log(x)-\cos(x))</tex> | <tex>f(x) = -(\log(x)-\cos(x))</tex> | ||
| - | <tex>\eps = | + | <tex>\eps = 10^{-5}</tex><br> |
| + | Начальное приближение <tex> x_0 = 1</tex><br> | ||
1. Метод простой итерации с <tex>s(x) = 1</tex>.<br> | 1. Метод простой итерации с <tex>s(x) = 1</tex>.<br> | ||
| - | 2. Метод простой итерации с <tex>s(x) = x</tex>.<br> | + | Сходимость за 28 шагов.<br> |
| + | 2. Метод простой итерации с <tex>s(x) = \sin x</tex>.<br> | ||
| + | Сходимость за 21 шаг.<br> | ||
3. Ускоренный метод простой итерации.<br> | 3. Ускоренный метод простой итерации.<br> | ||
| + | Сходимость за 3 шага.<br> | ||
4. Метод Вегстейна.<br> | 4. Метод Вегстейна.<br> | ||
| + | Сходимость за 3 шага.<br><br><br> | ||
| + | <tex>f(x) = -(\frac{1}{2}+x^2-\cos x)</tex> | ||
| + | Корень <tex>x_* \approx 0.58 </tex><br> | ||
| + | <tex>\eps = 10^{-5}</tex><br> | ||
| + | Начальное приближение <tex> x_0 = 1</tex><br> | ||
| + | 1. Метод простой итерации с <tex>s(x) = 1</tex>.<br> | ||
| + | Сходимость за 23 шагов.<br> | ||
| + | 2. Метод простой итерации с <tex>s(x) = \sin x</tex>.<br> | ||
| + | Сходимость за 5 шаг.<br> | ||
| + | 3. Ускоренный метод простой итерации.<br> | ||
| + | Сходимость за 4 шага.<br> | ||
| + | 4. Метод Вегстейна.<br> | ||
| + | Сходимость за 4 шага.<br><br><br> | ||
| + | <tex>f(x) = -(\frac{1}{2}+x^2-\cos x)</tex> | ||
| + | Корень <tex>x_* \approx 0.58 </tex><br> | ||
| + | <tex>\eps = 10^{-8}</tex><br> | ||
| + | Начальное приближение <tex> x_0 = 0.4</tex><br> | ||
| + | 1. Метод простой итерации с <tex>s(x) = 1</tex>.<br> | ||
| + | Сходимость за 43 шагов.<br> | ||
| + | 2. Метод простой итерации с <tex>s(x) = \sin x</tex>.<br> | ||
| + | Сходимость за 7 шагов.<br> | ||
| + | 3. Ускоренный метод простой итерации.<br> | ||
| + | Сходимость за 5 шагов.<br> | ||
| + | 4. Метод Вегстейна.<br> | ||
| + | Сходимость за 7 шагов.<br> | ||
| + | |||
| + | |||
| + | Исходный код можно скачать [[Media:PowerIterationMethod.zip|Код программы]] | ||
== Заключение == | == Заключение == | ||
== Ссылки == | == Ссылки == | ||
Текущая версия
Содержание |
Постановка задачи
Пусть есть функция .
Требуется найти корень этой функции: такой при котором
Решение необходимо найти численно, то есть для реализации на ЭВМ. Для решения этой задачи предлагается использовать метод простых итераций.
Метод простых итераций в общем виде
Заменим исходное уравнение на эквивалентное
,и будем строить итерации по правилу
. Таким образом метод простой итерации - это одношаговый итерационный процесс. Для того, что бы начать данный процесс, необходимо знать начальное приближение
. Выясним условия сходимости метода и выбор начального приближения.
Сходимость метода простых итераций
Метод сходится, если при последовательность {
} имеет предел.
Обозначим окресность точки
радиуса
, то есть
.
Теорема 1. Если липшиц-непрерывна с константой
на
, то есть выполняется
при этом если также выполнено
где - точное решение.
Из оценки видно, что метод линеен.
Пусть непрерывно дифференцируема на
, тогда из теоремы вытекают следующие утверждения:
Следствие 1. Если для
, выполнено
, и
, тогда уравнение
имеет единственное решение на
и метод простой итерации сходится к решению.
Следствие 2. Если уравнение имеет решение
,
непрерывно дифференцируема на
и
. Тогда существует
такое, что на
уравнение не имеет других решений и метод простой итерации сходится к решению при
Геометрическая интерпретация
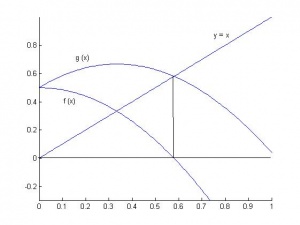
Рассмотрим график функции . Это озночает, что решение уравнения
и
- это точка пересечения
с прямой
:
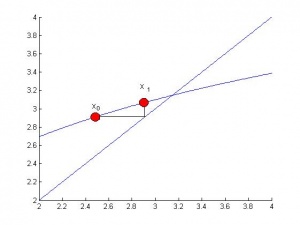
И следующая итерация - это координата
пересечения горизонтальной прямой точки
с прямой
.
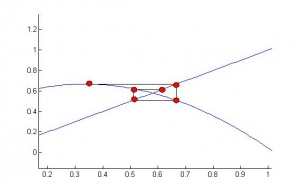
Из рисунка наглядно видно требование сходимости . Чем ближе производная
к
, тем быстрее сходится алгоритм. В зависимости от знака производной вблизи решения приближения могут строится по разному. Если
, то каждое следующее приближение строится с другой стороны от корня:
Метод релаксации
Так как для сходимости метода очень важен выбор функцииГде не меняет знака на отрезке, на котором ищется корень функции.
Положим и рассмотрим метод в этом случае.
Тогда получим метод 'релаксации':
для которого , и метод сходится при условии
Пусть в некоторой окресности корня выполняются условия
Тогда метод релаксации сходится при
Выбор параметра
Оценим погрешность метода релаксации
Применяя теорему о среднем получаем
Отсюда
Следовательно
Таким образом задача сводится к нахождению минимума функции
Из рассмотрения графика функции видно, что точка минимума определяется
и равна
Ускорение сходимости
Как следует из Теоремы 1, метод простых итераций линеен, то есть
Воспользуемся этим для оценки погрешности на каждой итерации. Запомним 3 последние итерации и выпишем их оценки:
Где нам известны (вычисленны по какому то линейному алгоритму),а
найдем из системы. Получим:
Метод ускорения сходимости заключается в том, что после вычисления 3 приближений по линейно сходящемуся алгоритму, вычисляется новое приближение по уточняющему правилу (2).
Применительно к методу релаксации имеем:
Следовательно
Можно показать, что данный метод имеет уже квадратичную скорость сходимости.
Метод Вегстейна
Метод Вегстейна, вообще говоря, является модификацией метода секущих, однако его можно назвать и улучшенным методом простой итерации, преобразовав вычислительню формулу
к виду
Это двухшаговый метод, и для начала вычислений необходимо задать 2 приближения .
Программная реализация
Все методы были реализованы на языке C++. Доступ к методам осуществяется через класс
PowerIterationMethod
пример кода:
PowerIterationMethod::PowerIterationParams *params =
new PowerIterationMethod::PowerIterationParams (
f1 // Исходная функция
,s1 // Функция s(x) в формусле (1) или константа в методе релаксации
,1 // Начальное приближение
,0 // Второе приближение для метода Вегстейна
,0 // Допустимая погрешность решения
,1000 // Максимальное количество итераций
);
PowerIterationMethod *method = new PowerIterationMethod (params);
method->simpleIteration (); // Вычисление по методу простой итерации
printf ("%f\n",method->getResult ());
printf ("%f",method->getEps ());
Примеры тестирования
Ошибкой будем считать и проверим скорость сходимости методов относительно друг друга.
Начальное приближение
1. Метод простой итерации с .
Сходимость за 28 шагов.
2. Метод простой итерации с .
Сходимость за 21 шаг.
3. Ускоренный метод простой итерации.
Сходимость за 3 шага.
4. Метод Вегстейна.
Сходимость за 3 шага.
Корень
Начальное приближение
1. Метод простой итерации с .
Сходимость за 23 шагов.
2. Метод простой итерации с .
Сходимость за 5 шаг.
3. Ускоренный метод простой итерации.
Сходимость за 4 шага.
4. Метод Вегстейна.
Сходимость за 4 шага.
Корень
Начальное приближение
1. Метод простой итерации с .
Сходимость за 43 шагов.
2. Метод простой итерации с .
Сходимость за 7 шагов.
3. Ускоренный метод простой итерации.
Сходимость за 5 шагов.
4. Метод Вегстейна.
Сходимость за 7 шагов.
Исходный код можно скачать Код программы
Заключение
Ссылки
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
- Н.Н.Калиткин. Численные методы. Москва «Наука», 1978.

