Критерий Вальда-Вольфовица
Материал из MachineLearning.
(Различия между версиями)
| (6 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
==Описание критерия== | ==Описание критерия== | ||
| - | Критерий серий Вальда-Вольфовица может быть использован как тест для [[анализа | + | Критерий серий Вальда-Вольфовица может быть использован как тест для [[Анализ регрессионных остатков (пример)|анализа регрессионных остатков]] наряду с [[Критерий Уилкоксона-Манна-Уитни|критерием Уилкоксона-Манна-Уитни]], [[Критерий Зигеля-Тьюки|критерием Зигеля-Тьюки]], [[Критерий знаков|критерием знаков]], [[Критерий экстремумов|критерием экстремумов]].<br> |
| - | В этом случае критерий серий Вальда-Вольфовица | + | В этом случае критерий серий Вальда-Вольфовица используется для проверки гипотезы H<sub>0</sub>: <tex>\varepsilon_{i}</tex> - независимая, одинаково распределенная сл. величина, где <tex>\varepsilon_{i}=y_{i}-\hat{y_{i}}</tex><br> |
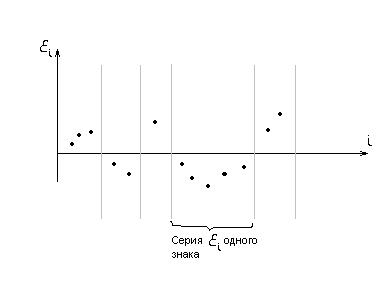
При анализе регресионных остатков будем выделять их в серии одного знака<br> | При анализе регресионных остатков будем выделять их в серии одного знака<br> | ||
[[Изображение:Vald-volf.JPG]]<br> | [[Изображение:Vald-volf.JPG]]<br> | ||
N<sub>s</sub> - число серий <tex>\sim</tex> N(EN<sub>s</sub>,DN<sub>s</sub>)<br> | N<sub>s</sub> - число серий <tex>\sim</tex> N(EN<sub>s</sub>,DN<sub>s</sub>)<br> | ||
<tex>E\varepsilon_{i}=0</tex><br> | <tex>E\varepsilon_{i}=0</tex><br> | ||
| - | <tex>EN_{s}=\frac{2n_{1}n_{2}}{n_{1}n_{2}}+1</tex>, где<br> | + | <tex>EN_{s}=\frac{2n_{1}n_{2}}{n_{1}+n_{2}}+1</tex>, где<br> |
n<sub>1</sub> - число <tex>\varepsilon_{i}\geq0</tex><br> | n<sub>1</sub> - число <tex>\varepsilon_{i}\geq0</tex><br> | ||
n<sub>2</sub> - число <tex>\varepsilon_{i}<0</tex><br> | n<sub>2</sub> - число <tex>\varepsilon_{i}<0</tex><br> | ||
| Строка 12: | Строка 12: | ||
Тогда по критерию серий Вальда-Вольфовица:<br> | Тогда по критерию серий Вальда-Вольфовица:<br> | ||
<tex>\frac{N_{s}-EN_{s}}{\sqrt{DN_{s}}}\sim N(0,1)</tex><br> | <tex>\frac{N_{s}-EN_{s}}{\sqrt{DN_{s}}}\sim N(0,1)</tex><br> | ||
| - | Исходя из полученного значения H<sub>0</sub> применяется при неком уровне значимости или | + | Исходя из полученного значения H<sub>0</sub> применяется при неком уровне значимости или отвергается. |
==Смотри также== | ==Смотри также== | ||
| - | + | * [[Регрессионный анализ]] | |
| + | * [[Анализ регрессионных остатков]] | ||
| + | * [[Анализ регрессионных остатков (пример)]] | ||
| + | * [[Статистический анализ данных (курс лекций, К.В.Воронцов)/2008]] | ||
| + | ==Литература== | ||
| + | # Дерфелль К. Статистика в аналитической химии. — М.: Мир,1994. - 170 с. | ||
[[Категория:Энциклопедия анализа данных]] | [[Категория:Энциклопедия анализа данных]] | ||
| - | [[Категория: | + | [[Категория:Регрессионный анализ]] |
Текущая версия
Описание критерия
Критерий серий Вальда-Вольфовица может быть использован как тест для анализа регрессионных остатков наряду с критерием Уилкоксона-Манна-Уитни, критерием Зигеля-Тьюки, критерием знаков, критерием экстремумов.
В этом случае критерий серий Вальда-Вольфовица используется для проверки гипотезы H0: - независимая, одинаково распределенная сл. величина, где
При анализе регресионных остатков будем выделять их в серии одного знака
Ns - число серий N(ENs,DNs)
, где
n1 - число
n2 - число
Тогда по критерию серий Вальда-Вольфовица:
Исходя из полученного значения H0 применяется при неком уровне значимости или отвергается.
Смотри также
- Регрессионный анализ
- Анализ регрессионных остатков
- Анализ регрессионных остатков (пример)
- Статистический анализ данных (курс лекций, К.В.Воронцов)/2008
Литература
- Дерфелль К. Статистика в аналитической химии. — М.: Мир,1994. - 170 с.