Теория измерений
Материал из MachineLearning.
(Новая: '''Теория измерений''' – это теория о классификации переменных величин по природе информации, которая ...) |
(орфография) |
||
| (4 промежуточные версии не показаны) | |||
| Строка 1: | Строка 1: | ||
| - | '''Теория измерений''' – это теория о классификации переменных величин по природе информации, которая содержится в числах – значениях этих переменных величин. Происхождение переменной величины накладывает ограничения на множество действий, которые можно производить с этой величиной. Иными словами, для каждой переменной величины существует ''' | + | '''Теория измерений''' – это теория о классификации переменных величин по природе информации, которая содержится в числах – значениях этих переменных величин. Происхождение переменной величины накладывает ограничения на множество действий, которые можно производить с этой величиной. Иными словами, для каждой переменной величины существует '''класс допустимых преобразований''' ('''КДП'''), которые корректно применимы ко всем значениям этой величины. |
Классификация величин по измеримости была предложена С.С.Стивенсом в 1946 году. Каждая группа величин, имеющих общие допустимые преобразования, называется шкалой измерений. | Классификация величин по измеримости была предложена С.С.Стивенсом в 1946 году. Каждая группа величин, имеющих общие допустимые преобразования, называется шкалой измерений. | ||
| Строка 45: | Строка 45: | ||
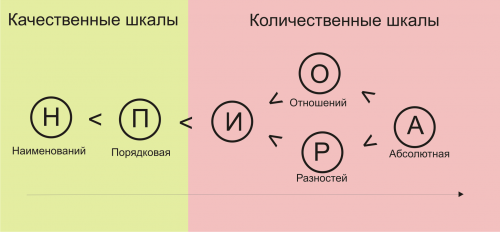
[[Изображение:Scales.png|thumb|right|500px|Иерархия шкал измерений. Слева - самая слабая шкала, справа - самая сильная.]] | [[Изображение:Scales.png|thumb|right|500px|Иерархия шкал измерений. Слева - самая слабая шкала, справа - самая сильная.]] | ||
| - | Все шкалы делят также на 2 большие группы: '''качественные''' и '''количественные'''. К качественным шкалам относят номинальную и порядковую, к | + | Все шкалы делят также на 2 большие группы: '''качественные''' и '''количественные'''. К качественным шкалам относят номинальную и порядковую, к количественным - все остальные. Это разделение показывает разницу в природе шкал: например, невозможно утверждать, что школьная оценка 2 настолько же хуже оценки 4, насколько 3 хуже оценки 5, поэтому порядковые шкалы относят к качественным. В то же время, для тел разной массы аналогичное утверждение корректно: тело массой 5 кг настолько же тяжелее тела массой 3 кг, насколько тело массой 4 кг тяжелей тела массой 2 кг. Таким образом, шкалы отношений - это количественные шкалы. |
| - | Очевидно, что КДП одной шкалы может полностью включать в себя КДП другой. Тогда говорят, что | + | Очевидно, что КДП одной шкалы может полностью включать в себя КДП другой. Тогда говорят, что вторая шкала сильнее первой. На иллюстрации изображена иерархия шкал. |
| + | |||
| + | == Шкалы измерений и анализ данных == | ||
| + | |||
| + | При [[Анализ данных|анализе данных]] следует помнить о том, к какой шкале измерений относятся исследуемые величины: | ||
| + | |||
| + | * Алгоритм анализа данных должен быть инвариантен относительно '''КДП''' исследуемой величины | ||
| + | * Алгоритм, применимый к более слабой шкале, применим и к более сильной. | ||
== Ссылки == | == Ссылки == | ||
*[http://en.wikipedia.org/wiki/Scales_of_measurement Wikipedia] | *[http://en.wikipedia.org/wiki/Scales_of_measurement Wikipedia] | ||
*[http://www.aup.ru/books/m163/1_1_2.htm Орлов А.И Прикладная статистика] | *[http://www.aup.ru/books/m163/1_1_2.htm Орлов А.И Прикладная статистика] | ||
| + | |||
| + | [[Категория:Прикладная статистика]] | ||
Текущая версия
Теория измерений – это теория о классификации переменных величин по природе информации, которая содержится в числах – значениях этих переменных величин. Происхождение переменной величины накладывает ограничения на множество действий, которые можно производить с этой величиной. Иными словами, для каждой переменной величины существует класс допустимых преобразований (КДП), которые корректно применимы ко всем значениям этой величины.
Классификация величин по измеримости была предложена С.С.Стивенсом в 1946 году. Каждая группа величин, имеющих общие допустимые преобразования, называется шкалой измерений.
Содержание |
Шкалы измерений
Номинальная шкала
В шкале наименований допустимыми являются все взаимно-однозначные преобразования. В этой шкале числа используются как метки, только для различения объектов. В шкале наименований измерены, например, номера телефонов, автомашин, паспортов, студенческих билетов. Пол людей тоже измерен в шкале наименований, результат измерения принимает два значения - мужской, женский. Очевидно, что не имеет смысла складывать номера телефонов или умножать серии паспортов.
КДП: биективные преобразования.
Порядковая шкала
В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между объектами. Простейшим примером являются оценки знаний учащихся. Заметим, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе ровно тот же смысл выражается словесно - неудовлетворительно, удовлетворительно, хорошо, отлично. Этим подчеркивается "нечисловой" характер оценок знаний учащихся. В порядковой шкале допустимыми являются все строго монотонные преобразования.
КДП: все строго монотонные преобразования.
Шкала интервалов
По шкале интервалов измеряют величину потенциальной энергии или координату точки на прямой. В этих случаях на шкале нельзя отметить ни естественное начало отсчета, ни естественную единицу измерения. Исследователь должен сам задать точку отсчета и сам выбрать единицу измерения. Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования, т.е. линейные функции. Температурные шкалы Цельсия и Фаренгейта связаны именно такой зависимостью: °C = 5/9 (°F - 32), где °C - температура (в градусах) по шкале Цельсия, а °F - температура по шкале Фаренгейта.
КДП: все преобразования вида
Шкала отношений
В шкалах отношений есть естественное начало отсчета - нуль, но нет естественной единицы измерения. По шкале отношений измерены большинство физических единиц: масса тела, длина, заряд, а также цены в экономике. Допустимыми преобразованиями шкале отношений являются подобные (изменяющие только масштаб). Другими словами, линейные возрастающие преобразования без свободного члена. Примеры использования таких преобразований: пересчет цен из одной валюты в другую по фиксированному курсу, перевод массы из килограмм в фунты.
КДП: все преобразования вида
Шкала разностей
В шкале разностей есть естественная единица измерения, но нет естественного начала отсчета. Время измеряется по шкале разностей, если год (или сутки - от полудня до полудня) принимаем естественной единицей измерения, и по шкале интервалов в общем случае. На современном уровне знаний естественного начала отсчета времени указать нельзя. Допустимыми преобразованиями шкале разностей являются сдвиги.
КДП: все преобразования вида
Абсолютная шкала
Только для абсолютной шкалы результаты измерений - числа в обычном смысле слова. Примером является число людей в комнате. Для абсолютной шкалы допустимым является только тождественное преобразование.
КДП:
Иерархия шкал измерений
Все шкалы делят также на 2 большие группы: качественные и количественные. К качественным шкалам относят номинальную и порядковую, к количественным - все остальные. Это разделение показывает разницу в природе шкал: например, невозможно утверждать, что школьная оценка 2 настолько же хуже оценки 4, насколько 3 хуже оценки 5, поэтому порядковые шкалы относят к качественным. В то же время, для тел разной массы аналогичное утверждение корректно: тело массой 5 кг настолько же тяжелее тела массой 3 кг, насколько тело массой 4 кг тяжелей тела массой 2 кг. Таким образом, шкалы отношений - это количественные шкалы.
Очевидно, что КДП одной шкалы может полностью включать в себя КДП другой. Тогда говорят, что вторая шкала сильнее первой. На иллюстрации изображена иерархия шкал.
Шкалы измерений и анализ данных
При анализе данных следует помнить о том, к какой шкале измерений относятся исследуемые величины:
- Алгоритм анализа данных должен быть инвариантен относительно КДП исследуемой величины
- Алгоритм, применимый к более слабой шкале, применим и к более сильной.