Экспоненциальное сглаживание
Материал из MachineLearning.
(→Ссылки) |
|||
| (3 промежуточные версии не показаны) | |||
| Строка 53: | Строка 53: | ||
== Проблемы == | == Проблемы == | ||
Модель работает только при небольшом горизонте прогнозирования. | Модель работает только при небольшом горизонте прогнозирования. | ||
| - | Не учитываются [[Тренд|тренд]] и [[Сезонность|сезонные]] изменения. Чтобы учесть их влияние, предлагается использовать модели: [[Модель Хольта| Хольта]] (учитывается линейный тренд) [[Модель Хольта-Уинтерса| Хольта-Уинтерса]] (мультипликативные экспоненциальный тренд и сезонность), [[Модель Тейла- | + | Не учитываются [[Тренд|тренд]] и [[Сезонность|сезонные]] изменения. Чтобы учесть их влияние, предлагается использовать модели: [[Модель Хольта| Хольта]] (учитывается линейный тренд) [[Модель Хольта-Уинтерса| Хольта-Уинтерса]] (мультипликативные экспоненциальный тренд и сезонность), [[Модель Тейла-Вейджа| Тейла-Вейджа]] (аддетивные линейный тренд и сезонность). |
== Литература== | == Литература== | ||
| Строка 74: | Строка 74: | ||
[http://en.wikipedia.org/wiki/Exponential_smoothing The exponential moving average] | [http://en.wikipedia.org/wiki/Exponential_smoothing The exponential moving average] | ||
| - | [[Категория: | + | [[Категория:Регрессионный анализ]] |
| + | [[Категория:Прогнозирование временных рядов]] | ||
[[Категория:Прикладная статистика]] | [[Категория:Прикладная статистика]] | ||
[[Категория:Энциклопедия анализа данных]] | [[Категория:Энциклопедия анализа данных]] | ||
Текущая версия
|
Выявление и анализ тенденции временного ряда часто производится с помощью его выравнивания или сглаживания. Экспоненциальное сглаживание — один из простейших и распространенных приемов выравнивания ряда. Экспоненциальное сглаживание можно представить как фильтр, на вход которого последовательно поступают члены исходного ряда, а на выходе формируются текущие значения экспоненциальной средней.
Пусть - временной ряд.
Экспоненциальное сглаживание ряда осуществляется по рекуррентной формуле:
,
.
Чем меньше α, тем в большей степени фильтруются, подавляются колебания исходного ряда и шума.
Если последовательно использовать рекуррентное это соотношение, то экспоненциальную среднюю можно выразить через значения временного ряда X.
.
Если к моменту начала сглаживания существуют более ранние данные, то в качестве начального
значения можно использовать арифметическую среднюю всех имеющихся данных или какой-то их части.
После появления работ Р. Брауна экспоненциальное сглаживание часто используется для решения задачи краткосрочного прогнозирования временных рядов.
Постановка задачи
Пусть задан временной ряд: .
Необходимо решить задачу прогнозирования временного ряда, т.е. найти
- горизонт прогнозирования, необходимо, чтобы
Для того, чтобы учитывать устаревание данных, введем невозрастающую последовательность весов
, тогда
Модель Брауна
Предположим, что D - невелико (краткосрочный прогноз), то для решения такой задачи используют модель Брауна .
.
Если рассматривать прогноз на 1 шаг вперед, то - погрешность этого прогноза, а новый прогноз
получается в результате корректировки предыдущего прогноза с учетом его ошибки - суть адаптации.
При краткосрочном прогнозировании желательно как можно быстрее отразить новые изменения и в то же время как можно лучше «очистить» ряд от случайных колебаний.
Т.о. следует увеличивать вес более свежих наблюдений: .
С другой стороны, для сглаживания случайных отклонений, α нужно уменьшить: .
Т.о. эти два требования находятся в противоречии. Поиск компромиссного значения α составляет задачу оптимизации модели. Обычно, α берут из интервала (0,1/3).
Примеры
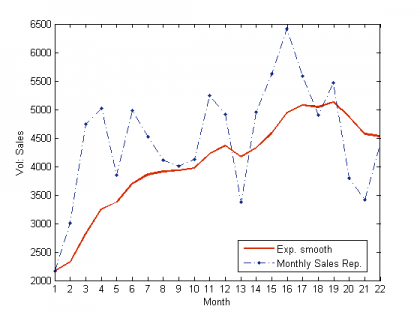
Работа экспоненциального сглаживания при α=0.2 на данных ежемесячных отчетов по продажам иностранной автомобильной марки в России за период с января 2007 по октябрь 2008. Отметим резкие падения в январе и феврале, когда продажи традиционно снижаются и повышения в начале лета.
Проблемы
Модель работает только при небольшом горизонте прогнозирования. Не учитываются тренд и сезонные изменения. Чтобы учесть их влияние, предлагается использовать модели: Хольта (учитывается линейный тренд) Хольта-Уинтерса (мультипликативные экспоненциальный тренд и сезонность), Тейла-Вейджа (аддетивные линейный тренд и сезонность).
Литература
Лукашин Ю. П. Адаптивные методы краткосрочного прогнозирования временных рядов. — М.: Финансы и статистика, 2003.
Brown R.G. Smoothing forecasting and prediction of discrete time series. - N.Y., 1963.
Brown R.G., Meyer R.F. The fundamental theorum of exponential smoothing. Oper. Res. - 1961. - Vol.9. -№ 5.
См. также
Модель Хольта — учитываются линейный тренд без сезонности.
Модель Хольта-Уинтерса — учитываются мультипликативный тренд и сезонность.
Модель Тейла-Вейджа — учитываются аддитивный тренд и сезонность.