EM алгоритм (пример)
Материал из MachineLearning.
м (sum_{n=1}^K -> sum_{k=1}^K) |
|||
| (22 промежуточные версии не показаны) | |||
| Строка 4: | Строка 4: | ||
==Постановка задачи разделения смеси гауссовых распределений== | ==Постановка задачи разделения смеси гауссовых распределений== | ||
Задана выборка <tex>X^{l}</tex> случайных и независимых наблюдений из смеси <tex>p(x)</tex> ,в которой описание <tex>i</tex> -ого элемента есть вектор <tex>x_{i} \in R^{n}</tex> . | Задана выборка <tex>X^{l}</tex> случайных и независимых наблюдений из смеси <tex>p(x)</tex> ,в которой описание <tex>i</tex> -ого элемента есть вектор <tex>x_{i} \in R^{n}</tex> . | ||
| - | Принята модель, в которой каждая компонента смеси есть гауссина с параметрами <tex>\mu</tex> и <tex>\Sigma</tex>, и известно число компонент смеси - <tex>K</tex> | + | Принята модель, в которой каждая компонента смеси есть гауссина с параметрами <tex>\mu</tex> и <tex>\Sigma</tex>, и известно число компонент смеси - <tex>K</tex>, |
| - | <center><tex>p(x)=\sum_{ | + | <center><tex>p(x)=\sum_{k=1}^K \pi_{k}\aleph(x|\mu_{k},\Sigma_{k})</tex>.</center> |
| - | Требуется оценить вектор параметров <tex>\theta=(\pi_{1},...,\pi_{k};\mu_{1},...,\mu_{k};\Sigma_{1},...,\Sigma_{k})</tex>, доставляющий максим функции правдоподобия | + | Требуется оценить вектор параметров <tex>\theta=(\pi_{1},...,\pi_{k};\mu_{1},...,\mu_{k};\Sigma_{1},...,\Sigma_{k})</tex>, доставляющий максим функции правдоподобия, |
| - | <center><tex>\ln p(X|\pi,\mu,\Sigma)= \sum_{n=1}^N \ln \{ \sum_{k=1}^K \pi_{k}\aleph(x_{n}|\mu_{k},\Sigma_{k})\}</tex></center> | + | <center><tex>\ln p(X|\pi,\mu,\Sigma)= \sum_{n=1}^N \ln \{ \sum_{k=1}^K \pi_{k}\aleph(x_{n}|\mu_{k},\Sigma_{k})\}</tex>.</center> |
==Алгоритм отыскания оптимальных параметров== | ==Алгоритм отыскания оптимальных параметров== | ||
| - | Оптимальные параметры отыскиваются последовательно с помощью итерационного EM-алгоритма. Основная идея – вводится вспомогательный вектор скрытых переменных. Это позволяет свести сложную оптимизационную задачу к последовательности итераций по пересчету коэффициентов (скрытых переменных по текущему приближению вектора параметров - E-шаг) и максимизации правдоподобия (с целью найти следующее приближение вектора - М-шаг. | + | Оптимальные параметры отыскиваются последовательно с помощью итерационного EM-алгоритма. Основная идея – вводится вспомогательный вектор скрытых переменных. Это позволяет свести сложную оптимизационную задачу к последовательности итераций по пересчету коэффициентов (скрытых переменных по текущему приближению вектора параметров - E-шаг) и максимизации правдоподобия (с целью найти следующее приближение вектора - М-шаг). |
| - | # В начале работы алгоритма задаются параметры начального приближения, которые в данной статье получаются в результате работы алгоритма | + | # В начале работы алгоритма задаются параметры начального приближения, которые в данной статье получаются в результате работы алгоритма kMeans. (Данная эвристика применяется, так как kMeans требуется намного меньше итераций до достижения стабилизации, в то время как каждый шаг EM требует больших вычислительных затрат). |
# Далее итеративно выполняется следующая пара процедур: | # Далее итеративно выполняется следующая пара процедур: | ||
| - | *E-шаг: используя текущее значение вектора параметров <tex>\theta=(\pi_{1},...,\pi_{k};\mu_{1},...,\mu_{k};\Sigma_{1},...,\Sigma_{k})</tex>, вычисляем значение вектора скрытых переменных <tex>\gamma</tex> | + | *E-шаг: используя текущее значение вектора параметров <tex>\theta=(\pi_{1},...,\pi_{k};\mu_{1},...,\mu_{k};\Sigma_{1},...,\Sigma_{k})</tex>, вычисляем значение вектора скрытых переменных <tex>\gamma</tex>, |
| - | <center><tex>\gamma_{nk}=\frac{\pi_{k}\aleph(x_{n}|\mu_{k},\Sigma_{k})}{\sum_{j=1}^K \pi_{j}\aleph(x_{n}|\mu_{j},\Sigma_{j})}</tex></center> | + | <center><tex>\gamma_{nk}=\frac{\pi_{k}\aleph(x_{n}|\mu_{k},\Sigma_{k})}{\sum_{j=1}^K \pi_{j}\aleph(x_{n}|\mu_{j},\Sigma_{j})}</tex>.</center> |
| - | *М-шаг: переоценка вектора параметров, используя текущее значение вектора скрытых переменных | + | *М-шаг: переоценка вектора параметров, используя текущее значение вектора скрытых переменных, |
| - | <center><tex>\mu^{new}_{k}=\frac{1}{N_{k}}\sum_{n=1}^N \gamma_{nk}x_{n}</tex></center> | + | <center><tex>\mu^{new}_{k}=\frac{1}{N_{k}}\sum_{n=1}^N \gamma_{nk}x_{n}</tex>,</center> |
| - | <center><tex>\Sigma^{new}_{k}=\frac{1}{N_{k}}\sum_{n=1}^N \gamma_{nk | + | <center><tex>\Sigma^{new}_{k}=\frac{1}{N_{k}}\sum_{n=1}^N \gamma_{nk} (x_{n}-\mu_{k}^{new})(x_{n}-\mu_{k}^{new})^{T}</tex>,</center> |
| - | <center><tex>\pi_{k}^{new}=\frac{N_{k}}{N}</tex></center> | + | <center><tex>\pi_{k}^{new}=\frac{N_{k}}{N}</tex>,</center> |
| - | <center><tex>N_{k}=\sum_{n=1}^N \gamma_{nk}</tex | + | <center><tex>N_{k}=\sum_{n=1}^N \gamma_{nk}</tex>, где <tex>\delta_{max}>\Delta</tex>.</center> |
| - | Процедура останавливается после того, как норма разности векторов скрытых переменных на каждой итерации не будет превышать заданную константу | + | Процедура останавливается после того, как норма разности векторов скрытых переменных на каждой итерации не будет превышать заданную константу, |
| - | <center><tex>\delta_{max}=max{\delta_{max},|\gamma_{nk}-\gamma^{0}_{nk}|}</tex></center> | + | <center><tex>\delta_{max}=max{\{\delta_{max},|\gamma_{nk}-\gamma^{0}_{nk}|\}}</tex>.</center> |
==Пример на модельных данных== | ==Пример на модельных данных== | ||
Продемонстрирована работа алгоритма на серии реальных и синтетических данных. | Продемонстрирована работа алгоритма на серии реальных и синтетических данных. | ||
| - | 1) Old Faithful – гидродинамический гейзер в Yellowstone National Park. Данные содержат информацию о 272-х извержениях, каждое из которых есть пара характеризующая длительность извержения и время до следующего извержения (в минутах). Ссылка на данные. [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/ | + | 1) Old Faithful – гидродинамический гейзер в Yellowstone National Park. Данные содержат информацию о 272-х извержениях, каждое из которых есть пара характеризующая длительность извержения и время до следующего извержения (в минутах). Ссылка на данные. [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/EM-Algorithm(Final)/Old%20Faithful.txt Old Faithful] |
[[Изображение:old_faithful.png|300px]] | [[Изображение:old_faithful.png|300px]] | ||
| Строка 165: | Строка 165: | ||
[[Изображение:hard_data_result.png|300px]] | [[Изображение:hard_data_result.png|300px]] | ||
| - | На рисунке приведены результаты работы алгоритма на данных, изображенных на рисунке выше. Стоит заметить, что даже при сильном взаимном проникновении классов, алгоритм показывает достойный результат. Интересным является также правильная классификация нескольких точек, находящихся «глубоко» в чужом классе. | + | На рисунке приведены результаты работы алгоритма на данных, изображенных на рисунке выше. Стоит заметить, что даже при сильном взаимном проникновении классов, алгоритм показывает достойный результат. Интересным является также правильная классификация нескольких точек, находящихся «глубоко» в чужом классе. На самом деле это зависит от положения центров кластеров и их формы. |
| + | |||
==Исходный код== | ==Исходный код== | ||
| - | *Cкачать листинги алгоритмов можно здесь [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/ | + | *Cкачать листинги алгоритмов можно здесь [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Spirin2009EMAlgorithm/ ExpMin.m], [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Spirin2009EMAlgorithm/ kMeansParam.m], [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Spirin2009EMAlgorithm/ DistMatrix.m]. |
| + | |||
==Смотри также == | ==Смотри также == | ||
| + | *[[Media:Nikita_Spirin_EM_Report_Final.pdf|Эта статья в формате PDF]] | ||
*[[Media:Nikita_Spirin_EM_Report.doc|Эта статья в формате Docx]] | *[[Media:Nikita_Spirin_EM_Report.doc|Эта статья в формате Docx]] | ||
| - | |||
*[[EM-алгоритм с последовательным добавлением компонент | EM-алгоритм с последовательным добавлением компонент]] | *[[EM-алгоритм с последовательным добавлением компонент | EM-алгоритм с последовательным добавлением компонент]] | ||
| + | *[[Функции радиального базиса (пример) | Функции радиального базиса]] | ||
| + | *[[Однослойный персептрон (пример) | Однослойный персептрон]] | ||
| + | *[[Прогнозирование плотности | Прогнозирование плотности]] | ||
==Литература== | ==Литература== | ||
*К. В. Воронцов, Лекции по статистическим (байесовским) алгоритмам классификации | *К. В. Воронцов, Лекции по статистическим (байесовским) алгоритмам классификации | ||
| - | *C.M. Bishop, Pattern Recognition and Machine Learning | + | *C.M. Bishop, "Pattern Recognition and Machine Learning" |
| + | * [http://www.inference.phy.cam.ac.uk/mackay/itila/ David J.C. MacKay, "Information Theory, Inference, and Learning Algorithms"] | ||
| + | *Jordan M. I., Xu L. Convergence results for the EM algorithm to mixtures of experts architectures: Tech. Rep. A.I. Memo No. 1458: MIT, Cambridge, MA, 1993. | ||
| + | *Шлезингер М., Главач В. Десять лекций по статистическому и структурному распознаванию. - Киев: Наукова думка, 2004. ISBN 966-00-0341-2 | ||
| - | [[Категория: | + | {{ЗаданиеВыполнено|Никита Спирин|В.В.Стрижов|28 мая 2009|Nikita Spirin|Strijov}} |
| - | [[Категория: | + | [[Категория:Практика и вычислительные эксперименты]] |
| + | [[Категория:Оценивание вероятностных распределений]] | ||
| + | [[Категория:Байесовская теория классификации]] | ||
[[Категория:Библиотеки алгоритмов]] | [[Категория:Библиотеки алгоритмов]] | ||
Текущая версия
EM алгоритм - общий метод нахождения оценок функции правдоподобия в моделях со скрытыми переменными. В данной статье рассматривается интерпретация смеси гауссовых распределений в терминах дискретных скрытых переменных.
Помимо того, что смеси распределений позволяют строить (приближать) сложные вероятностные распеределения, с их помощью можно так же решать задачу кластеризации данных. Далее мы будем решать задачу кластеризации с помощью ЕМ алгоритма, предварительно приблизив решение алгоритмом kMeans.
Содержание |
Постановка задачи разделения смеси гауссовых распределений
Задана выборка случайных и независимых наблюдений из смеси
,в которой описание
-ого элемента есть вектор
.
Принята модель, в которой каждая компонента смеси есть гауссина с параметрами
и
, и известно число компонент смеси -
,
Требуется оценить вектор параметров , доставляющий максим функции правдоподобия,
Алгоритм отыскания оптимальных параметров
Оптимальные параметры отыскиваются последовательно с помощью итерационного EM-алгоритма. Основная идея – вводится вспомогательный вектор скрытых переменных. Это позволяет свести сложную оптимизационную задачу к последовательности итераций по пересчету коэффициентов (скрытых переменных по текущему приближению вектора параметров - E-шаг) и максимизации правдоподобия (с целью найти следующее приближение вектора - М-шаг).
- В начале работы алгоритма задаются параметры начального приближения, которые в данной статье получаются в результате работы алгоритма kMeans. (Данная эвристика применяется, так как kMeans требуется намного меньше итераций до достижения стабилизации, в то время как каждый шаг EM требует больших вычислительных затрат).
- Далее итеративно выполняется следующая пара процедур:
- E-шаг: используя текущее значение вектора параметров
, вычисляем значение вектора скрытых переменных
,
- М-шаг: переоценка вектора параметров, используя текущее значение вектора скрытых переменных,
Процедура останавливается после того, как норма разности векторов скрытых переменных на каждой итерации не будет превышать заданную константу,
Пример на модельных данных
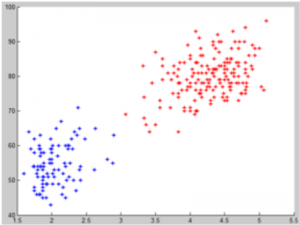
Продемонстрирована работа алгоритма на серии реальных и синтетических данных. 1) Old Faithful – гидродинамический гейзер в Yellowstone National Park. Данные содержат информацию о 272-х извержениях, каждое из которых есть пара характеризующая длительность извержения и время до следующего извержения (в минутах). Ссылка на данные. Old Faithful
На графике выше показаны иcходные данные. По оси x отложено значение одного признака (время извержения в мин.), по оси y – соответственно значение второго признака. Цвет точек означает принадлежность к тому или иному классу.
% Load the data from local directory load 'Old Faithful.txt' %------------------Invoke the EM-Algorithm k=2; % set the number of classes w = ExpMin(Old_Faithful,k,2); %----------------Plot classified data h = figure; hold on idx1 = find(w.y == 1); % object indices for the 1st class idx2 = find(w.y == 2); plot(w.x(idx1,1), w.x(idx1,2), 'r*'); plot(w.x(idx2,1), w.x(idx2,2), 'b*');
Классы определены алгоритмом абсолютно (ошибок нет), сложность задачи - легкая, так как видно что классы линейно-разделимы и расстояние между центрами классов велико.
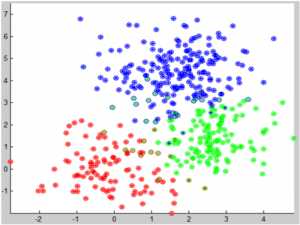
2) Синтетические данные (легкий случай, 3 класса)
N = 100; % 1st class contains N objects alpha = 1.5; % 2st class contains alpha*N ones beta = 2; % 3rd class contains beta*N ones sig23 = 1; % assume 2nd and 3rd classes have the same variance as the 1st dist2 = 2.5; dist3 = 2.0; N2 = floor(alpha * N); % calculate the size of the 2nd class N3 = floor(beta * N); % calculate the size of the 2nd class cls1X = randn(N, 2); % generate random objects of the 1st class % generate a random distance from the center of the 1st class to the center % of the 2nd and 3rd ShiftClass2 = repmat(dist2 * [sin(pi*rand) cos(pi*rand)],[N2,1]); ShiftClass3 = repmat(dist3 * [sin(pi*rand) 2*cos(pi*rand)],[N3,1]); % generate random objects of the 2nd class cls2X = sig23 * randn(N2, 2) + ShiftClass2; cls3X = sig23 * randn(N3, 2) + ShiftClass3; % combine the objects X = [cls1X; cls2X; cls3X]; % assign class labels: 1s and 2s and 3s y = [zeros(size(cls1X,1),1)+1; zeros(size(cls2X,1),1)+2; zeros(size(cls3X,1),1)+3]; %end X; y; % note that y contains only 1s and 2s and 3s idx1 = find(y == 1); % object indices for the 1st class idx2 = find(y == 2); idx3 = find(y == 3); %-------------------plot sample data h = figure; hold on plot(X(idx1,1), X(idx1,2), 'r*'); plot(X(idx2,1), X(idx2,2), 'g*'); plot(X(idx3,1), X(idx3,2), 'b*'); axis tight xlabel('x_1'); ylabel('x_2'); %------------------Invoke the EM-Algorithm k=3; % set the number of classes w = ExpMin(X,k,2); %----------------Plot classified data idx1 = find(w.y == 1); % object indices for the 1st class idx2 = find(w.y == 2); idx3 = find(w.y == 3); plot(w.x(idx1,1), w.x(idx1,2), 'ro'); plot(w.x(idx2,1), w.x(idx2,2), 'go'); plot(w.x(idx3,1), w.x(idx3,2), 'bo');
В данном примере заметно небольшое взаимное проникновение классов друг в друга, что влечет к частично ошибочной классификации (метки в результате работы алгоритма EM сравниваются с известными). Аналогично предыдущему примеру по оси абсцисс значение первого признака, по оси ординат – второго. Цвет – принадлежность классу.
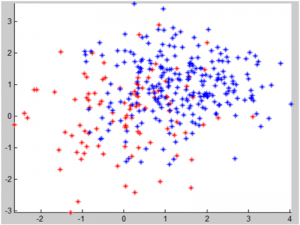
3) Синтетические данные (тяжелый случай, 2 класса)
N = 100; % 1st class contains N objects alpha = 2.5; % 2st class contains alpha*N ones sig2 = 1; % assume 2nd class has the same variance as the 1st dist2 = 1.5; N2 = floor(alpha * N); % calculate the size of the 2nd class cls1X = randn(N, 2); % generate random objects of the 1st class % generate a random distance from the center of the 1st class to the center % of the 2nd ShiftClass2 = repmat(dist2 * [sin(pi*rand) cos(pi*rand)],[N2,1]); % generate random objects of the 2nd class cls2X = sig2 * randn(N2, 2) + ShiftClass2; % combine the objects X = [cls1X; cls2X]; % assign class labels: 0s and 1s y = [zeros(size(cls1X,1),1); ones(size(cls2X,1),1)]; %------------------------------------------------------------end X; y; % note that y contains only 1s and 0s idx1 = find(y == 0); % object indices for the 1st class idx2 = find(y == 1); %-------------------------------plot sample data h = figure; hold on plot(X(idx1,1), X(idx1,2), 'r*'); plot(X(idx2,1), X(idx2,2), 'b*'); axis tight xlabel('x_1'); ylabel('x_2'); % close(h); %---------------------------------------Invoke the EM-Algorithm k=2; % set the number of classes w = ExpMin(X,k,2); %------------------------------------------Plot classified data idx1 = find(w.y == 1); % object indices for the 1st class idx2 = find(w.y == 2); plot(w.x(idx1,1), w.x(idx1,2), 'ro'); plot(w.x(idx2,1), w.x(idx2,2), 'bo');
Отображение исходных данных с истинными метками классов
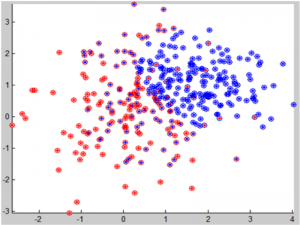
На рисунке приведены результаты работы алгоритма на данных, изображенных на рисунке выше. Стоит заметить, что даже при сильном взаимном проникновении классов, алгоритм показывает достойный результат. Интересным является также правильная классификация нескольких точек, находящихся «глубоко» в чужом классе. На самом деле это зависит от положения центров кластеров и их формы.
Исходный код
- Cкачать листинги алгоритмов можно здесь ExpMin.m, kMeansParam.m, DistMatrix.m.
Смотри также
- Эта статья в формате PDF
- Эта статья в формате Docx
- EM-алгоритм с последовательным добавлением компонент
- Функции радиального базиса
- Однослойный персептрон
- Прогнозирование плотности
Литература
- К. В. Воронцов, Лекции по статистическим (байесовским) алгоритмам классификации
- C.M. Bishop, "Pattern Recognition and Machine Learning"
- David J.C. MacKay, "Information Theory, Inference, and Learning Algorithms"
- Jordan M. I., Xu L. Convergence results for the EM algorithm to mixtures of experts architectures: Tech. Rep. A.I. Memo No. 1458: MIT, Cambridge, MA, 1993.
- Шлезингер М., Главач В. Десять лекций по статистическому и структурному распознаванию. - Киев: Наукова думка, 2004. ISBN 966-00-0341-2
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |