Классификация пациентов с сердечно-сосудистыми заболеваниями (отчет)
Материал из MachineLearning.
(→Описание данных) |
|||
| (96 промежуточных версий не показаны.) | |||
| Строка 4: | Строка 4: | ||
=== Цель проекта === | === Цель проекта === | ||
| - | Цель | + | Цель проекта — классификация пациентов с подозрением на сердечно-сосудистые заболевания по группам риска. |
=== Обоснование проекта === | === Обоснование проекта === | ||
| Строка 10: | Строка 10: | ||
=== Описание данных === | === Описание данных === | ||
| - | Дан список пациентов с указанием их группы риска(по экспертной оценке) и результатов их анализов по 20 параметрам. | + | Дан список 100 пациентов с указанием их группы риска (по экспертной оценке) и результатов их анализов по 20 параметрам. |
=== Критерии качества === | === Критерии качества === | ||
| - | + | Критериями качества являются общее количество ошибок классификации и критерий скользящего контроля Leave One Out. | |
| - | + | При этом не допускается более 1 ошибки для пациентов групп риска A1 (уже прооперированные больные) | |
| + | и A3 (больные с высокой вероятностью заболевания). | ||
=== Требования к проекту === | === Требования к проекту === | ||
| - | + | Алгоритм не должен допускать более одной ошибки по группам риска A1 и A3, а также минимальное количество ошибок по остальным группам риска. | |
=== Выполнимость проекта === | === Выполнимость проекта === | ||
| - | + | Особенностями данных, которые могут затруднить выполнение проекта, являются малое количество прецедентов по некоторым группам риска (в особенности A2) и наличие пропусков в данных (только 66 пациентов не имеют пропусков в данных). | |
=== Используемые методы === | === Используемые методы === | ||
| - | Предполагается, | + | Предполагается использовать линейные алгоритмы классификации, в частности SVM.== Постановка задачи == |
| - | + | Дана обучающая выборка <tex>X^\ell = (x_i, y_i)_{i=1}^\ell, ~~ \ell = 66</tex>, где | |
| - | == | + | <tex>x_i \in \mathbb{R}^n, n = 20</tex>, <tex>y_i \in \{A_1, A_3, B_1, B_2\}</tex>. |
| + | Для каждой из задач двуклассовой классификации(отделение одного класса от трех остальных и отделение пар классов друг от друга) перекодируем классы так, что <tex>y_i \in \{-1, 1\}</tex>. Требуется подобрать вектор параметров <tex>\mathbf{w}</tex> оптимальной разделяющей гиперплоскости, который минимизирует функционал скользящего контроля: <center><tex>LOO(\mathbf{w},X^\ell) = \sum_{i=1}^\ell [a(x_i, X^\ell\backslash x_i, \mathbf{w}) \neq y_i] \rightarrow \min_{\mathbf{w}}</tex>, где <tex>a(x) = [\sum_{j=1}^n w_jx^j-w_0 > 0]</tex></center> | ||
== Описание алгоритмов == | == Описание алгоритмов == | ||
| - | |||
| - | |||
=== Базовые предположения === | === Базовые предположения === | ||
| + | Особенностью данной задачи является большая размерность признакового пространства и малое число прецедентов. | ||
| + | Таким образом для того, чтобы избегнуть переобучения и добиться устойчивой классификации, требуется решить задачу отбора признаков. Для этой цели предполагается использовать алгоритм Relevance Kernel Machine with supervised selectivity (далее - <tex>\mu - RKM</tex>), который совмещает в себе возможности решения задачи классификации и отбора признаков. | ||
| - | === Математическое описание === | + | === Математическое описание алгоритмов === |
| + | ==== Квази-вероятностная постановка задачи ==== | ||
| + | Пусть <tex>\Omega</tex> - множество объектов, каждый из которых принадлежит одному из двух классов: <tex>y(\omega) \in Y = \{-1, 1\}</tex>. Каждый объект <tex>\omega \in \Omega</tex> характеризуется <tex>n</tex> признаками в некоторых шкалах | ||
| + | <tex>x^i(\omega) \in X_i</tex>. Пусть в пространстве признаков <tex>X = X_1 \times \dots \times X_n</tex> объективно определена некоторая неизвестная гиперплоскость <tex>\sum_{i=1}^n K_i(\vartheta_i, x^i) + b = 0</tex>. В качестве модели распределения объектов рассмотрим два несобственных параметрических распределения: | ||
| + | |||
| + | <tex>\varphi_{+1}(x^1, \dots, x^n | \vartheta_1, | ||
| + | \dots, \vartheta_n, b) = \left\{ | ||
| + | \begin{array}{l} | ||
| + | 1, ~ \sum_{i=1}^n K_i(\vartheta_i, x^i) + b \ge 1, \\ | ||
| + | \exp{\bigl[-c\bigl(1 - \sum_{i=1}^n K_i(\vartheta_i, x^i) - b \bigr)\bigr]}, ~ \sum_{i=1}^n K_i(\vartheta_i, x^i) + b < 1, \\ | ||
| + | \end{array} | ||
| + | \right.</tex> | ||
| + | <tex>\varphi_{-1}(x^1, \dots, x^n | \vartheta_1, | ||
| + | \dots, \vartheta_n, b) = \left\{ | ||
| + | \begin{array}{l} | ||
| + | 1, ~ \sum_{i=1}^n K_i(\vartheta_i, x^i) + b \le -1, \\ | ||
| + | \exp{\bigl[-c\bigl(1 + \sum_{i=1}^n K_i(\vartheta_i, x^i) + b \bigr)\bigr]}, ~ \sum_{i=1}^n K_i(\vartheta_i, x^i) + b > -1. \\ | ||
| + | \end{array} | ||
| + | \right.</tex> | ||
| + | |||
| + | Далее вектор <tex>(\vartheta_1, \dots, \vartheta_n, b)</tex> рассмотрим как случайный вектор с априорной плотностью распределения <tex>\Psi(\vartheta_1, \dots, \vartheta_n, b).</tex> По формуле Байеса апостериорная плотность распределения параметров <tex>\mathbf{\vartheta}</tex> и <tex>b</tex>: <center><tex>P\bigl(\mathbf{\vartheta}, b| X^{\ell}\bigr)\prop \Psi(\mathbf{\vartheta}, b) \biggl(\prod_{j: y_j = +1} \varphi_{+1}(\mathbf{x_j} | \mathbf{\vartheta}, | ||
| + | b)\biggr)\biggl(\prod_{j: y_j = -1} \varphi_{-1}(\mathbf{x_j} | | ||
| + | \mathbf{\vartheta}, b)\biggr)</tex></center> | ||
| + | |||
| + | Согласно принципу максимизации апостериорной плотности распределения: | ||
| + | <center><tex>\bigl(\hat{\vartheta_1}, \dots, \hat{\vartheta_n}, \hat{b}\bigr) = arg \max_{\mathbf{\vartheta}, b} \biggl[\ln \Psi(\mathbf{\vartheta}, b) + \sum_{j: y_j = +1} \ln \varphi_{+1}(\mathbf{x_j} | \mathbf{\vartheta}, | ||
| + | b) + \sum_{j: y_j = -1} \ln \varphi_{-1}(\mathbf{x_j} | \mathbf{\vartheta}, | ||
| + | b)\biggr]</tex></center> | ||
| + | |||
| + | ==== Метод <tex>\mu - RKM</tex> ==== | ||
| + | Пусть априорные плотности распределения компонент <tex>\vartheta_i</tex> направляющего вектора разделяющей гиперплоскости имеют нормальные распределения с нулевыми математическими ожиданиями и дисперсиями <tex>r_i</tex>: <center><tex>\psi(\vartheta_i|r_i) = \frac{1}{\sqrt{2\pi r_i}}\exp\bigl(-\frac{1}{2r_i}K_i(\vartheta_i, \vartheta_i)\bigr)</tex></center> | ||
| + | Будем считать, что параметр <tex>b</tex> имеет равномерное несобственное распределение, равное единице на всей числовой оси. | ||
| + | Тогда плотность распределения вектора <tex>\mathbf{\vartheta}</tex> пропорциональна: | ||
| + | <center><tex>\Psi(\vartheta_1, \dots, \vartheta_n|r_1, \dots, r_n) \prop \bigl(\prod_{i=1}^n r_i\bigr)^{-1/2}\exp\bigl(-\sum_{i=1}^n\frac{1}{2r_i}K_i(\vartheta_i, \vartheta_i)\bigr)</tex></center> | ||
| + | Положим, что все величины <tex>\frac{1}{r_i}</tex> имеют априорное гамма распределение: | ||
| + | <center><tex>\gamma(\frac{1}{r_i}|\alpha,\beta) \prop (1/r_i)^{\alpha - 1} \exp(-\beta(1/r_i))</tex>.</center> | ||
| + | Примем что <tex>\alpha = \frac{(1 + \mu)^2}{2\mu}, \beta = \frac{1}{2\mu}</tex>, где <tex>\mu</tex> - некоторый неотрицательный параметр. | ||
| + | |||
| + | |||
| + | Принцип максимизации совместной апостериорной плотности приводит к критерию обучения: | ||
| + | <center><tex>\left\{\sum_{i=1}^n \bigl[\frac{1}{r_i}\bigl(K_i(\vartheta_i, \vartheta_i) + \frac{1}{\mu}\bigr) + \bigl( \frac{1}{\mu} + 1 + \mu \bigr)\bigr] + C\sum_{j=1}^{\ell} \delta_j \to \min(\mathbf{\vartheta}, \mathbf{r}, b, \mathbf{\delta}), \\ | ||
| + | y_j\biggl(\sum_{i=1}^n K_i\bigl(\vartheta_i, x_i(\omega_j)\bigr)\biggr) \ge 1 - \delta_j, ~ \delta_j \ge 0, j = 1, \dots, \ell. | ||
| + | \right.</tex></center> | ||
| + | |||
| + | Для каждой итерации при фиксированном приближении(<tex>r_i^k, i = 1, \dots, n</tex>) решение данной оптимизационной задачи сводится лишь к небольшой модификации классического SVM. | ||
| + | Если же найдено текущее приближение <tex>(\vartheta_1^k, \dots, \vartheta_n^k, b^k)</tex>, то следующее приближение <tex>r_1^{k+1}, \dots, r_n^{k+1}</tex> может быть найдено из простого соотношения: <center><tex>r_i^{k+1} = \frac{K_i(\vartheta_i, \vartheta_i) + \frac{1}{\mu}}{\frac{1}{\mu} + 1 + \mu}</tex></center> | ||
| + | |||
| + | ====Отбор признаков==== | ||
| + | Для повышения устойчивости алгоритма был применен дополнительный отбор признаков. Для этого производился предварительный запуск алгоритма RKM и рассматривался полученный вектор весов признаков: <tex>\hat{r}_i, i = 1, \dots, n</tex>. | ||
| + | Далее из набора признаков удалялись те из них , для которых <tex>\frac{\max_j ~ \hat{r}_j}{\hat{r}_i} > \gamma, i = 1, \dots, n</tex>, где <tex>\gamma</tex> - дополнительный параметр селективности. На модифицированном наборе признаков алгоритм RKM запускался еще раз для получения окончательной классификации. | ||
=== Варианты или модификации === | === Варианты или модификации === | ||
| + | Параметрами алгоритма являются <tex>C \in [0, \infty], ~ \mu \in [0, \infty], ~ \gamma \in [1, \infty]</tex>, наилучшие значения которых требуется выбрать в результате эксперимента. | ||
| - | == Описание системы == | + | ==Описание системы== |
| - | + | Описание системы находится в файле [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Panov2009Cardio/ Systemdocs.docx] | |
| - | + | Файлы системы можно скачать здесь: | |
| + | [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group674/Panov2009Cardio/ SelRKM.m, GetRelevantFeatures.m, GetStatsIfClassification.m] | ||
== Отчет о вычислительных экспериментах == | == Отчет о вычислительных экспериментах == | ||
| + | <source lang="matlab"> | ||
| + | % OneVsOthersTest - script which tests RKM algorithm cardiovascular diseases train set | ||
| + | % in problems of classification one class vs 3 other classes | ||
| + | % Author: Maxim Panov, MIPT, group 674 | ||
| + | % | ||
| + | % Input: excel-files with objects-features matrices of 4 types of patients | ||
| + | % | ||
| + | % Output: | ||
| + | % statistics - 4 x 3 x 4 structure: | ||
| + | % statistics(k, j, i) - statistics of classification(with fields like | ||
| + | % in output of GetStatsOfClassification) of class i | ||
| + | % with selectivityLevel 0.1*10^k and C = 100*10^j | ||
| + | |||
| + | %% Upload data | ||
| + | UploadData; | ||
| + | trainSet = allData; | ||
| + | types = [repmat(1, size(a1, 1), 1); | ||
| + | repmat(2, size(a3, 1), 1); | ||
| + | repmat(3, size(b1, 1), 1); | ||
| + | repmat(4, size(b2, 1), 1)]; | ||
| + | |||
| + | %% Set selectivity rate | ||
| + | selectivityRate = 10; | ||
| - | === | + | %% Compute statistics of classification |
| + | for i = 1 : 4 | ||
| + | supplTrainSet = [trainSet(types == i, :); trainSet(types ~= i, :)]; | ||
| + | supplTypes = [repmat(1, size(types(types == i, :), 1), 1); repmat(-1, size(types(types ~= i, :), 1), 1)]; | ||
| + | C = 100; | ||
| + | for j = 1 : 3 | ||
| + | C = C * 10; | ||
| + | selectivity = 0.1; | ||
| + | for k = 1 : 4 | ||
| + | selectivity = selectivity * 10; | ||
| + | supplStatisticsA(k, 1) = GetStatsOfClassification(supplTrainSet, supplTypes, C, selectivity, selectivityRate); | ||
| + | end | ||
| + | if j == 1 | ||
| + | supplStatisticsB = supplStatisticsA; | ||
| + | else | ||
| + | supplStatisticsB = cat(2, supplStatisticsB, supplStatisticsA); | ||
| + | end | ||
| + | end | ||
| + | if i == 1 | ||
| + | statistics = supplStatisticsB; | ||
| + | else | ||
| + | statistics = cat(3, statistics, supplStatisticsB); | ||
| + | end | ||
| + | |||
| + | end | ||
| + | </source> | ||
=== Анализ качества работы алгоритма === | === Анализ качества работы алгоритма === | ||
| - | + | На основании полученных результатов для каждой из четырех подзадач классификации можно выбрать наилучшие значения параметров, статистика классификации для которых приведена в таблице: | |
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Class | ||
| + | ! C | ||
| + | ! SelectivityLevel | ||
| + | ! SelectivityRate | ||
| + | ! Relevant features | ||
| + | ! Test error | ||
| + | ! LOO | ||
| + | |- | ||
| + | | A1 | ||
| + | | 10000 | ||
| + | | 1000 | ||
| + | | 30 | ||
| + | | 1, 3, 6, 7, 9 ,10, 12, 14, 19 | ||
| + | | 5 | ||
| + | | 15 | ||
| + | |- | ||
| + | | A3 | ||
| + | | 10000 | ||
| + | | 1000 | ||
| + | | 30 | ||
| + | | 2, 3, 5, 7 ,9, 12, 14, 15, 20 | ||
| + | | 0 | ||
| + | | 5 | ||
| + | |- | ||
| + | | B1 | ||
| + | | 10000 | ||
| + | | 1000 | ||
| + | | 10 | ||
| + | | 2, 3, 4 ,7 ,12 ,18 | ||
| + | | 23 | ||
| + | | 23 | ||
| + | |- | ||
| + | | B2 | ||
| + | | 100000 | ||
| + | | 100 | ||
| + | | 30 | ||
| + | | 2, 3, 6, 7 , 9, 10, 12, 15 | ||
| + | | 11 | ||
| + | | 20 | ||
| + | |} | ||
| - | == | + | ===Параметры классификатора=== |
| + | Решающее правило при классификации на 2 класса методом <tex>\mu - RKM</tex> задается следующей формулой: <tex>y(\omega) = sign\biggl[\sum_{j: \lambda_j > 0} \lambda_j y_j\sum_{i=1}^n r_i x_i(\omega_j)x_i(\omega) + b\biggr]</tex>. | ||
| - | + | Параметры <tex>\mathbf{\lambda}, \mathbf{r}</tex>, <tex>b</tex>, а также номера отобранных признаков для задач отделения одного класса от остальных выложены здесь: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Cardio1/ parameters.mat] | |
| + | == Список литературы == | ||
| + | * К. В. Воронцов, Лекции по линейным алгоритмам классификации | ||
| + | * Татарчук А. И., Сулимова В.В., Моттль В.В., Уиндридж Д. Метод релевантных потенциальных функций для селективного комбинирования разнородной информации при обучении распознаванию образов на основе байесовского подхода // Всеросcийская конференция ММРО-14.М.: МАКС Пресс, 2009. | ||
| + | * Айзерман М.А., Браверман Э.М., Розоноэр Л.И. Метод потенциальных функций в теории обучения машин. М.: Наука, 1970, 384 с. | ||
| + | *Ross A., Jain A.K. Multimodal biometrics: An overview. Proceedings of the 12th European Signal Processing Conference (EUSIPCO), 2004. Vienna, Austria, pp. 1221-1224. | ||
| - | {{ | + | {{ЗаданиеВыполнено|Максим Панов|В. В. Стрижов|15 декабря 2009|Maxx|Strijov}} |
| + | [[Категория:Практика и вычислительные эксперименты]] | ||
__NOTOC__ | __NOTOC__ | ||
Текущая версия
Введение в проект
Описание проекта
Цель проекта
Цель проекта — классификация пациентов с подозрением на сердечно-сосудистые заболевания по группам риска.
Обоснование проекта
Полученные результаты могут быть использованы для предварительной диагностики заболевания у пациентов.
Описание данных
Дан список 100 пациентов с указанием их группы риска (по экспертной оценке) и результатов их анализов по 20 параметрам.
Критерии качества
Критериями качества являются общее количество ошибок классификации и критерий скользящего контроля Leave One Out. При этом не допускается более 1 ошибки для пациентов групп риска A1 (уже прооперированные больные) и A3 (больные с высокой вероятностью заболевания).
Требования к проекту
Алгоритм не должен допускать более одной ошибки по группам риска A1 и A3, а также минимальное количество ошибок по остальным группам риска.
Выполнимость проекта
Особенностями данных, которые могут затруднить выполнение проекта, являются малое количество прецедентов по некоторым группам риска (в особенности A2) и наличие пропусков в данных (только 66 пациентов не имеют пропусков в данных).
Используемые методы
Предполагается использовать линейные алгоритмы классификации, в частности SVM.== Постановка задачи ==
Дана обучающая выборка , где
,
.
Описание алгоритмов
Базовые предположения
Особенностью данной задачи является большая размерность признакового пространства и малое число прецедентов.
Таким образом для того, чтобы избегнуть переобучения и добиться устойчивой классификации, требуется решить задачу отбора признаков. Для этой цели предполагается использовать алгоритм Relevance Kernel Machine with supervised selectivity (далее - ), который совмещает в себе возможности решения задачи классификации и отбора признаков.
Математическое описание алгоритмов
Квази-вероятностная постановка задачи
Пусть - множество объектов, каждый из которых принадлежит одному из двух классов:
. Каждый объект
характеризуется
признаками в некоторых шкалах
. Пусть в пространстве признаков
объективно определена некоторая неизвестная гиперплоскость
. В качестве модели распределения объектов рассмотрим два несобственных параметрических распределения:
Согласно принципу максимизации апостериорной плотности распределения:
Метод 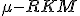
Пусть априорные плотности распределения компонент Будем считать, что параметр имеет равномерное несобственное распределение, равное единице на всей числовой оси.
Тогда плотность распределения вектора
пропорциональна:
Положим, что все величины имеют априорное гамма распределение:
Примем что , где
- некоторый неотрицательный параметр.
Принцип максимизации совместной апостериорной плотности приводит к критерию обучения:
Для каждой итерации при фиксированном приближении() решение данной оптимизационной задачи сводится лишь к небольшой модификации классического SVM.
Отбор признаков
Для повышения устойчивости алгоритма был применен дополнительный отбор признаков. Для этого производился предварительный запуск алгоритма RKM и рассматривался полученный вектор весов признаков: .
Далее из набора признаков удалялись те из них , для которых
, где
- дополнительный параметр селективности. На модифицированном наборе признаков алгоритм RKM запускался еще раз для получения окончательной классификации.
Варианты или модификации
Параметрами алгоритма являются , наилучшие значения которых требуется выбрать в результате эксперимента.
Описание системы
Описание системы находится в файле Systemdocs.docx Файлы системы можно скачать здесь: SelRKM.m, GetRelevantFeatures.m, GetStatsIfClassification.m
Отчет о вычислительных экспериментах
% OneVsOthersTest - script which tests RKM algorithm cardiovascular diseases train set % in problems of classification one class vs 3 other classes % Author: Maxim Panov, MIPT, group 674 % % Input: excel-files with objects-features matrices of 4 types of patients % % Output: % statistics - 4 x 3 x 4 structure: % statistics(k, j, i) - statistics of classification(with fields like % in output of GetStatsOfClassification) of class i % with selectivityLevel 0.1*10^k and C = 100*10^j %% Upload data UploadData; trainSet = allData; types = [repmat(1, size(a1, 1), 1); repmat(2, size(a3, 1), 1); repmat(3, size(b1, 1), 1); repmat(4, size(b2, 1), 1)]; %% Set selectivity rate selectivityRate = 10; %% Compute statistics of classification for i = 1 : 4 supplTrainSet = [trainSet(types == i, :); trainSet(types ~= i, :)]; supplTypes = [repmat(1, size(types(types == i, :), 1), 1); repmat(-1, size(types(types ~= i, :), 1), 1)]; C = 100; for j = 1 : 3 C = C * 10; selectivity = 0.1; for k = 1 : 4 selectivity = selectivity * 10; supplStatisticsA(k, 1) = GetStatsOfClassification(supplTrainSet, supplTypes, C, selectivity, selectivityRate); end if j == 1 supplStatisticsB = supplStatisticsA; else supplStatisticsB = cat(2, supplStatisticsB, supplStatisticsA); end end if i == 1 statistics = supplStatisticsB; else statistics = cat(3, statistics, supplStatisticsB); end end
Анализ качества работы алгоритма
На основании полученных результатов для каждой из четырех подзадач классификации можно выбрать наилучшие значения параметров, статистика классификации для которых приведена в таблице:
| Class | C | SelectivityLevel | SelectivityRate | Relevant features | Test error | LOO |
|---|---|---|---|---|---|---|
| A1 | 10000 | 1000 | 30 | 1, 3, 6, 7, 9 ,10, 12, 14, 19 | 5 | 15 |
| A3 | 10000 | 1000 | 30 | 2, 3, 5, 7 ,9, 12, 14, 15, 20 | 0 | 5 |
| B1 | 10000 | 1000 | 10 | 2, 3, 4 ,7 ,12 ,18 | 23 | 23 |
| B2 | 100000 | 100 | 30 | 2, 3, 6, 7 , 9, 10, 12, 15 | 11 | 20 |
Параметры классификатора
Решающее правило при классификации на 2 класса методом задается следующей формулой:
.
Параметры ,
, а также номера отобранных признаков для задач отделения одного класса от остальных выложены здесь: parameters.mat
Список литературы
- К. В. Воронцов, Лекции по линейным алгоритмам классификации
- Татарчук А. И., Сулимова В.В., Моттль В.В., Уиндридж Д. Метод релевантных потенциальных функций для селективного комбинирования разнородной информации при обучении распознаванию образов на основе байесовского подхода // Всеросcийская конференция ММРО-14.М.: МАКС Пресс, 2009.
- Айзерман М.А., Браверман Э.М., Розоноэр Л.И. Метод потенциальных функций в теории обучения машин. М.: Наука, 1970, 384 с.
- Ross A., Jain A.K. Multimodal biometrics: An overview. Proceedings of the 12th European Signal Processing Conference (EUSIPCO), 2004. Vienna, Austria, pp. 1221-1224.
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |

