Вероятностное пространство

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(дополнение)
(→Литература: категория)
 
(2 промежуточные версии не показаны)
Строка 19: Строка 19:
** <tex>0\le P(B)\le 1</tex> для любого <tex>B\in \mathcal{F}</tex>
** <tex>0\le P(B)\le 1</tex> для любого <tex>B\in \mathcal{F}</tex>
** <tex>P(\emptyset)=0</tex>, <tex>P(\Omega)=1</tex>
** <tex>P(\emptyset)=0</tex>, <tex>P(\Omega)=1</tex>
-
** Если <tex>A\in\mathcal{F}</tex> и <tex>B\in\mathcal{F}</tex> — события, причем <tex>A\cap B=\emptyset</tex>, тогда <tex>P(A\cup B)=P(A)+P(B)</tex> (свойство аддитивности).
+
** Если <tex>A\in\mathcal{F}</tex> и <tex>B\in\mathcal{F}</tex> — события, причем <tex>A\cap B=\emptyset</tex>, тогда <tex>P(A\cup B)=P(A)+P(B)</tex> ('''свойство аддитивности''').
-
** Если <tex>\{B_i\}_{i=1}^\infty\subset\mathcal{F}</tex>, причем Если <tex>B_i\cap B_j=\emptyset</tex> для любых Если <tex>i\ne j</tex>, тогда должно быть <tex>P\left(\bigcup_{i=1}^\infty B_i\right)=\sum_{i=1}^\infty P(B_i)</tex> (свойство сигма-аддитивности).
+
** Если <tex>\{B_i\}_{i=1}^\infty\subset\mathcal{F}</tex>, причем Если <tex>B_i\cap B_j=\emptyset</tex> для любых Если <tex>i\ne j</tex>, тогда должно быть <tex>P\left(\bigcup_{i=1}^\infty B_i\right)=\sum_{i=1}^\infty P(B_i)</tex> ('''свойство сигма-аддитивности''').
 +
 
 +
Заметим, что последнее свойство сигма-аддитивности меры эквивалентно (при условии выполнения всех прочих свойств, в том числе конечной аддитивности) любому из следующих свойств '''непрерывности меры''':
 +
 
 +
* Если <tex>A_i\in B</tex> и <tex>A_1\subseteq A_2\subseteq A_3\cdots</tex>, тогда <tex>P\left(\bigcup_{n=1}^\infty A_n\right)=\lim_{n\to\infty}P(A_n)</tex>.
 +
* Если <tex>A_i\in B</tex> и <tex>A_1\supseteq A_2\supseteq A_3\cdots</tex>, тогда <tex>P\left(\bigcap_{n=1}^\infty A_n\right)=\lim_{n\to\infty}P(A_n)</tex>.
 +
* Если <tex>A_i\in B</tex>, <tex>A_1\supseteq A_2\supseteq A_3\cdots</tex> и <tex>\bigcap_{n=1}^\infty A_n=\emptyset</tex>, тогда <tex>\lim_{n\to\infty}P(A_n)=0</tex>.
== Примеры наиболее часто использующихся вероятностных пространств ==
== Примеры наиболее часто использующихся вероятностных пространств ==
Строка 28: Строка 34:
Если множество элементарных исходов <tex>\Omega</tex> конечно или счетно: <tex>\Omega=\{\omega_1,\omega_2,\ldots\}</tex>, то соответствующее вероятностное пространство называется ''дискретным''. В случае дискретных вероятностных пространств событиями обычно считают все возможные подмножества <tex>\Omega</tex>. В этом случае для задания вероятности необходимо и достаточно приписать каждому элементарному исходу <tex>\omega_i</tex> число <tex>p_i\ge 0</tex> так, чтобы их сумма была равна 1. Тогда вероятность любого события <tex>B</tex> задается следующим образом:
Если множество элементарных исходов <tex>\Omega</tex> конечно или счетно: <tex>\Omega=\{\omega_1,\omega_2,\ldots\}</tex>, то соответствующее вероятностное пространство называется ''дискретным''. В случае дискретных вероятностных пространств событиями обычно считают все возможные подмножества <tex>\Omega</tex>. В этом случае для задания вероятности необходимо и достаточно приписать каждому элементарному исходу <tex>\omega_i</tex> число <tex>p_i\ge 0</tex> так, чтобы их сумма была равна 1. Тогда вероятность любого события <tex>B</tex> задается следующим образом:
-
<tex>P(B)=\sum_{i:\omega_i\in B}p_i.</tex>
+
<center><tex>P(B)=\sum_{i:\omega_i\in B}p_i.</tex></center>
 +
 
 +
Важным частным случаем такого пространства является '''классический способ задания вероятностей''', когда количество элементарных исходов конечно и все они имеют одинаковую вероятность. Тогда вероятность любого события определяется как отношение его мощности (т.е. количества элементарных исходов, ''благоприятствующих'' данному событию) к общему числу элементарных исходов:
 +
 
 +
<center><tex>P(B)=\frac{|B|}{|\Omega|}</tex>.</center>
 +
 
 +
Однако всегда необходимо помнить, что для того, чтобы применять данный способ, необходимо убедиться в том, что элементарные исходы действительно равновероятны. Это должно либо быть сформулировано как исходное условие, либо этот факт следует строго вывести из имеющихся начальных условий.
=== Вероятностные пространства на прямой <tex>\mathbb{R}</tex> ===
=== Вероятностные пространства на прямой <tex>\mathbb{R}</tex> ===
Строка 52: Строка 64:
}}
}}
-
[[Категория:Материалы по теории вероятностей]]
+
[[Категория:Теория вероятностей]]

Текущая версия

Вероятностное пространство — это математическая модель случайного эксперимента (опыта) в аксиоматике А. Н. Колмогорова. Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, необходимую для его математического анализа средствами теории вероятностей. Любая задача теории вероятностей решается в рамках некоторого вероятностного пространства, полностью заданного изначально. Задачи, в которых вероятностное пространство задано не полностью, а недостающую информацию следует получить по результатам наблюдений, относятся к области математической статистики.

Содержание

Определение

Вероятностное пространство — это тройка (\Omega,\mathcal{F},P), где:

  • \Omega — это множество объектов \omega\in\Omega, называемых элементарными исходами эксперимента. На это множество не накладывается никаких условий, оно может быть совершенно произвольным. При задании вероятностной модели для конкретного случайного эксперимента множество \Omega необходимо определять таким образом, чтобы в любой реализации опыта происходил один и только один элементарный исход. Элементарный исход содержит в себе всю возможную информацию о результате случайного опыта. С формальной математической точки зрения «произвести случайный опыт» означает в точности указать один элементарный исход \omega, который произошел в данной реализации опыта.
  • \mathcal{F} — это некоторая зафиксированная система подмножеств B\subset\Omega, которые будут называться (случайными) событиями. Если элементарный исход, произошедший в результате реализации случайного опыта, входит в событие B, то говорят, что в данной реализации событие B произошло, иначе говорят, что событие не произошло. Совокупность событий \mathcal{F} должна быть сигма-алгеброй, то есть удовлетворять следующим свойствам:
    • Пустое множество \emptyset должно быть событием, то есть принадлежать \mathcal{F}. Это событие, которое существует в любом вероятностном пространстве, называется невозможным, поскольку оно никогда не происходит.
    • Все множество \Omega также должно быть событием: \Omega\in\mathcal{F}. Это событие называется достоверным, так как происходит при любой реализации случайного опыта.
    • Совокупность событий \mathcal{F} должна образовывать алгебру, то есть быть замкнутой относительно основных теоретико-множественных операций, выполняемых над конечным числом событий. Если A\in\mathcal{F} и B\in\mathcal{F}, тогда должно быть A\cup B\in\mathcal{F}, A\cap B\in\mathcal{F}, \overline{A}\in\mathcal{F}. Операции над событиями имеют очевидный содержательный смысл.
    • В дополнение к указанным свойствам, система \mathcal{F} должна быть замкнута относительно операций над событиями, выполняемых в счетном числе (свойство сигма-алгебры). Если \{B_i\}_{i=1}^\infty\subset\mathcal{F}, тогда должно быть \bigcup_{i=1}^\infty B_i\in\mathcal{F} и \bigcap_{i=1}^\infty B_i\in\mathcal{F}.
  • P — это числовая функция, которая определена на \mathcal{F} и ставит в соответствие каждому событию B\in\mathcal{F} число P(B), которое называется вероятностью события B. Эта функция должна быть конечной сигма-аддитивной мерой, равной 1 на всем пространстве, то есть обладать свойствами:
    • 0\le P(B)\le 1 для любого B\in \mathcal{F}
    • P(\emptyset)=0, P(\Omega)=1
    • Если A\in\mathcal{F} и B\in\mathcal{F} — события, причем A\cap B=\emptyset, тогда P(A\cup B)=P(A)+P(B) (свойство аддитивности).
    • Если \{B_i\}_{i=1}^\infty\subset\mathcal{F}, причем Если B_i\cap B_j=\emptyset для любых Если i\ne j, тогда должно быть P\left(\bigcup_{i=1}^\infty B_i\right)=\sum_{i=1}^\infty P(B_i) (свойство сигма-аддитивности).

Заметим, что последнее свойство сигма-аддитивности меры эквивалентно (при условии выполнения всех прочих свойств, в том числе конечной аддитивности) любому из следующих свойств непрерывности меры:

  • Если A_i\in B и A_1\subseteq A_2\subseteq A_3\cdots, тогда P\left(\bigcup_{n=1}^\infty A_n\right)=\lim_{n\to\infty}P(A_n).
  • Если A_i\in B и A_1\supseteq A_2\supseteq A_3\cdots, тогда P\left(\bigcap_{n=1}^\infty A_n\right)=\lim_{n\to\infty}P(A_n).
  • Если A_i\in B, A_1\supseteq A_2\supseteq A_3\cdots и \bigcap_{n=1}^\infty A_n=\emptyset, тогда \lim_{n\to\infty}P(A_n)=0.

Примеры наиболее часто использующихся вероятностных пространств

Дискретные вероятностные пространства

Если множество элементарных исходов \Omega конечно или счетно: \Omega=\{\omega_1,\omega_2,\ldots\}, то соответствующее вероятностное пространство называется дискретным. В случае дискретных вероятностных пространств событиями обычно считают все возможные подмножества \Omega. В этом случае для задания вероятности необходимо и достаточно приписать каждому элементарному исходу \omega_i число p_i\ge 0 так, чтобы их сумма была равна 1. Тогда вероятность любого события B задается следующим образом:

P(B)=\sum_{i:\omega_i\in B}p_i.

Важным частным случаем такого пространства является классический способ задания вероятностей, когда количество элементарных исходов конечно и все они имеют одинаковую вероятность. Тогда вероятность любого события определяется как отношение его мощности (т.е. количества элементарных исходов, благоприятствующих данному событию) к общему числу элементарных исходов:

P(B)=\frac{|B|}{|\Omega|}.

Однако всегда необходимо помнить, что для того, чтобы применять данный способ, необходимо убедиться в том, что элементарные исходы действительно равновероятны. Это должно либо быть сформулировано как исходное условие, либо этот факт следует строго вывести из имеющихся начальных условий.

Вероятностные пространства на прямой 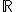\mathbb{R}

Вероятностные пространства на прямой (\Omega=\mathbb{R}) естественным образом возникают при изучении случайных величин. При этом в общем случае уже не получается рассматривать в качестве событий любые подмножества прямой, поскольку на таком широком классе обычно нельзя задать вероятностную меру, удовлетворяющую необходимым аксиомам. Универсальная сигма-алгебра событий, достаточная для работы - это сигма-алгебра борелевских множеств \mathcal{B}(\mathbb{R}): наименьшая сигма-алгебра, содержащая все открытые множества. Эквивалентное определение - наименьшая сигма-алгебра, содержащая все интервалы (a,b). Универсальный способ задания вероятностной меры на данной сигма-алгебре - через функцию распределения случайной величины.

Вероятностные пространства в конечномерном пространстве 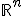\mathbb{R}^n

Вероятностные пространства с множеством элементарных исходов \Omega=\mathbb{R}^n естественным образом возникают при изучении случайных векторов. Универсальной сигма-алгеброй событий при этом также является борелевская сигма-алгебра \mathcal{B}(\mathbb{R}^n), порожденная всеми открытыми множествами. Принципиально этот случай мало чем отличается от случая одной прямой.

Вероятностные пространства в пространстве 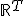\mathbb{R}^T для произвольного множества индексов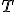 T

При изучении случайных процессов возникают более сложные вероятностные пространства с множеством элементарных исходов \mathbb{R}^T, где индексы T часто интерпретируются как "время". Чаще всего рассматривают случаи T=\{0,1,2,\ldots\} (процессы с дискретным временем) или T=(a,b), T=[0,\infty) (процессы с непрерывным временем).


Литература

1. Ширяев А.Н. Вероятность. — М.: МЦНМО, 2004.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%92%D0%B5%D1%80%D0%BE%D1%8F%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE»
Личные инструменты