Размерность Вапника-Червоненкиса
Материал из MachineLearning.
(Новая: {{Задание|DmitryKonstantinov|Константин Воронцов|8 января 2010}} == Определение == == Примеры вычисления размерности...) |
(дополнение, иллюстрации, литература) |
||
| Строка 1: | Строка 1: | ||
{{Задание|DmitryKonstantinov|Константин Воронцов|8 января 2010}} | {{Задание|DmitryKonstantinov|Константин Воронцов|8 января 2010}} | ||
| + | '''Размерность Вапника-Червоненкиса''' (ёмкость, VC-dimension) — | ||
== Определение == | == Определение == | ||
| - | == Примеры | + | Если существует число <tex>h</tex> такое, что [[Функция роста | функция роста]] <tex>\Delta A(h) = 2^h</tex> и <tex>\Delta A(h+1) < 2^{h+1}</tex>, то оно |
| + | называется '''ёмкостью''' или '''размерностью Вапника-Червоненкиса''' (VC-dimension) семейства алгоритмов <tex>A</tex>. Если такого числа <tex>h</tex> не существует, то говорят, что семейство <tex>A</tex> имеет бесконечную ёмкость. | ||
| + | |||
| + | Другая формулировка определения (через [[Разнообразие | разнообразие]]): Пусть задано множество объектов <tex>X</tex> и некоторое семейство функций (алгоритмов классификации, решающих правил) <tex>A</tex>, которые сопоставляют каждому объекту множества <tex>X</tex> один из двух заданных классов. Ёмкостью семейства <tex>A</tex> называется наибольшее число <tex>h</tex>, такое, что существует подмножество из <tex>h</tex> объектов в множестве <tex>X</tex>, которое функции из <tex>A</tex> могут разбить на два класса всеми возможными способами. Если же такие подмножества существуют для сколь угодно большого <tex>h</tex>, то ёмкость полагается равной бесконечности. | ||
| + | |||
| + | Если семейство алгоритмов имеет конечную размерность Вапника-Червоненкиса, то такое семейство называют классом Вапника-Червоненкиса. | ||
| + | == Примеры == | ||
| + | Как пример, рассмотрим задачу о разбиении точек на плоскости на два класса прямой линией — это так называемый линейный классификатор. Множество из любых трёх точек, не лежащих на одной прямой, может быть разделено прямой линией на два класса всеми возможными способами (2³ = 8 способами, на рисунке ниже показаны два из них), но множества из четырёх и более точек — уже нет. Поэтому размерность Вапника-Червоненкиса линейного классификатора на плоскости равна трём. | ||
| + | |||
| + | {| border="0" cellpadding="4" cellspacing="0" align="center" | ||
| + | | align="center" bgcolor=#ddffdd | [[Image:VC1.png]] | ||
| + | | align="center" bgcolor=#ddffdd | [[Image:VC2.png]] | ||
| + | <!--| align="center" bgcolor=#ddffdd | [[Image:VC3.png]] --> | ||
| + | | align="center" bgcolor=#ffdddd | [[Image:VC4.png]] | ||
| + | |- | ||
| + | | colspan="2" align="center" bgcolor=#ddffdd | '''Примеры разделения трёх<br />точек на два класса''' | ||
| + | | align="center" bgcolor=#ffdddd | '''Разделение невозможно<br />для этих четырёх точек''' | ||
| + | |} | ||
| + | |||
| + | В общем случае, размерность Вапника-Червоненкиса семейства линейных классификаторов в n-мерном пространстве равна n + 1. | ||
| + | |||
== Связь с размером обучающей выборки == | == Связь с размером обучающей выборки == | ||
| - | == | + | == Литература == |
| + | #{{книга | ||
| + | |автор = Вапник В.Н., Червоненкис А.Я. | ||
| + | |заглавие = Теория распознавания образов | ||
| + | |год = 1974 | ||
| + | |место = М. | ||
| + | |издательство = Наука | ||
| + | }} | ||
| + | # A. Blumer, A. Ehrenfeucht, D. Haussler, and M. K. Warmuth. "Learnability and the Vapnik–Chervonenkis dimension." Journal of the ACM, 36(4):929–865, 1989. | ||
| + | |||
| + | [[Категория:Теория вычислительного обучения]] | ||
Версия 18:57, 3 января 2010
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |
Размерность Вапника-Червоненкиса (ёмкость, VC-dimension) —
Содержание |
Определение
Если существует число такое, что функция роста
и
, то оно
называется ёмкостью или размерностью Вапника-Червоненкиса (VC-dimension) семейства алгоритмов
. Если такого числа
не существует, то говорят, что семейство
имеет бесконечную ёмкость.
Другая формулировка определения (через разнообразие): Пусть задано множество объектов и некоторое семейство функций (алгоритмов классификации, решающих правил)
, которые сопоставляют каждому объекту множества
один из двух заданных классов. Ёмкостью семейства
называется наибольшее число
, такое, что существует подмножество из
объектов в множестве
, которое функции из
могут разбить на два класса всеми возможными способами. Если же такие подмножества существуют для сколь угодно большого
, то ёмкость полагается равной бесконечности.
Если семейство алгоритмов имеет конечную размерность Вапника-Червоненкиса, то такое семейство называют классом Вапника-Червоненкиса.
Примеры
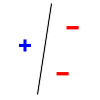
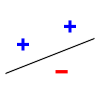
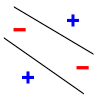
Как пример, рассмотрим задачу о разбиении точек на плоскости на два класса прямой линией — это так называемый линейный классификатор. Множество из любых трёх точек, не лежащих на одной прямой, может быть разделено прямой линией на два класса всеми возможными способами (2³ = 8 способами, на рисунке ниже показаны два из них), но множества из четырёх и более точек — уже нет. Поэтому размерность Вапника-Червоненкиса линейного классификатора на плоскости равна трём.
| 
| 
|
| Примеры разделения трёх точек на два класса | Разделение невозможно для этих четырёх точек | |
В общем случае, размерность Вапника-Червоненкиса семейства линейных классификаторов в n-мерном пространстве равна n + 1.
Связь с размером обучающей выборки
Литература
- Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. — М.: Наука, 1974.
- A. Blumer, A. Ehrenfeucht, D. Haussler, and M. K. Warmuth. "Learnability and the Vapnik–Chervonenkis dimension." Journal of the ACM, 36(4):929–865, 1989.

