Сеть радиальных базисных функций

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
Строка 50: Строка 50:
== Литература ==
== Литература ==
<references/>
<references/>
 +
 +
{{Задание|MariaAleshina|Константин Воронцов|5 января 2010}}

Версия 20:42, 5 января 2010

Радиальные функции — это функции f(x), зависящие только от расстояния между x и фиксированной точ- кой пространства X.

Гауссиан p_j(x) = N(x; \mu _j ,\Sigma _j) с диагональной матрицей \Sigma _j можно записать в виде

~p_j(x) = N_j exp(-1/2 \rho _j (x, \mu _j)

где N_j = (2\pi)^ {-n/2)(\sigma _{j1}, \dots ,\sigma _{jn})^{-1} — нормировочный множитель,
\rho _j(x, x') — взвешенная евклидова метрика в n-мерном пространстве X:
~\rho (x, x') = \sum ^n _{d = 1} \sigma ^{-2} _{jd} |\xi _d - \xi _d '| ,
x = (\xi _1, . . . ,\xi _n), x' = (\xi _1 ', . . . , \xi _n').

Чем меньше расстояние \rho _j(x, \mu _j), тем выше значение плотности в точке x. Поэтому плотность p _j(x) можно рассматривать как функцию близости вектора x к фиксированному центру \mu _j.

Содержание

Сеть радиальных базисных функций

Пусть Y = {1, . . . ,M}, каждый класс y \in Y имеет свою плотность распределения p_y(x) и представлен частью выборки X ^l _y = \{(x_i, y_i) \in X ^l | y_i = y \}.

Гипотеза

Функции правдоподобия классов p_y(x), y \in Y , представимы в виде смесей k_y компонент. Каждая компонента имеет n-мерную гауссовскую плотность с параметрами
\mu _{yj} = (\mu _{yj1}, \dots , \mu _{yjn}), \Sigma _{yj} = diag(\sigma _{yj1}, \dots , \sigma _{yjn})
j = 1, . . . , k_y:

p_y(x) = \sum ^{k _y} _{j = 1} \omega _{yj} p _{yj}(x), p_{yj}(x) = N(x; \mu _{yj} ,\Sigma _{yj}), \Sigma ^{k_y} _{j = 1} \omega _{yj} = 1, \omega _{yj} > 0;

Алгоритм классификации

Запишем байесовское решающее правило, выразив плотность каждой компоненты p_{yj}(x) через взвешенное евклидово расстояние от объекта x до центра компоненты \mu _{yj} :

a(x) = argmax _{y \in Y} \lambda _y P _y \sum ^{k_y} _{j = 1} N _{yj} exp(-1/2 \rho _{yj} (x, \mu _{yj}))

где N _{yj} = (2\pi)^{-n/2} (\sigma _{yj1},\dots , \sigma _{yjn})^{-1} — нормировочные множители. Алгоритм имеет вид суперпозиции, состоящей из трёх уровней или слоёв.
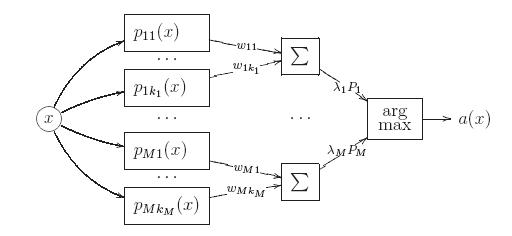
Изображение:NS.JPG
Первый слой образован k_1 + \dots+ k_M гауссианами p_{yj}(x), y \in Y , j = 1, \dots, k_y. На входе они принимают описание объекта x, на выходе выдают оценки близости объекта x к центрам \mu _{yj} , равные значениям плотностей компонент в точке x.
Второй слой состоит из M сумматоров, вычисляющих взвешенные средние этих оценок с весами w_{yj} . На выходе второго слоя появляются оценки принадлежности объекта x каждому из классов, равные значениям плотностей классов p_{yj}(x).
Третий слой образуется единственным блоком argmax, принимающим окончательное решение об отнесении объекта x к одному из классов.
Таким образом, при классификации объекта x оценивается его близость к каж- дому из центров \mu _{yj} по метрике \rho _{yj}(x, \mu _{yj}), j = 1, \dots, k_y. Объект относится к тому классу, к чьим центрам он располагается ближе.

Описанный трёхуровневый алгоритм классификации называется сетью c радиальными базисными функциями или RBF-сетью (radial basis function network). Это одна из разновидностей нейронных сетей.

Обучение RBF-сети

Обучение сводится к восстановлению плотности каждого из классов p_y(x) с помощью EM-алгоритма. Результатом обучения являются центры \mu _{yj} и дис- персии \Sigma _{yj} компонент j = 1, . . . , k_y. Интересно отметить, что, оценивая дисперсии, мы фактически подбираем метрики \rho _{yj} , с помощью которых будут вычисляться рас-стояния до центров \mu _{yj} . При использовании Алгоритма 1.4 для каждого класса определяется оптимальное число компонент смеси.[1]

Литература


Данная статья является непроверенным учебным заданием.
Студент: Участник:MariaAleshina
Преподаватель: Участник:Константин Воронцов
Срок: 5 января 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.


Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D0%B5%D1%82%D1%8C_%D1%80%D0%B0%D0%B4%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D1%85_%D0%B1%D0%B0%D0%B7%D0%B8%D1%81%D0%BD%D1%8B%D1%85_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B9»
Личные инструменты