Нормализация ДНК-микрочипов

Материал из MachineLearning.

(Различия между версиями)

Версия 06:22, 8 мая 2010

Нормализация - важный этап предобработки ДНК-микрочипов, позволяющий сделать несколько рассматриваемых в эксперименте чипов пригодными к сравнению между собой. Основная цель анализа на этом этапе - исключить влияние систематических небиологических различий между микрочипами. Источников таких различий множество: вариации эффективности обратной транскрипции, маркировки красителями, гибридизации, физические различия между чипами (повреждения, царапины), небольшие различия в концентрации реагентов, вариация лабораторных условий.

Парадигмы нормализации

Нормализация на все гены, нормализация на гены домашнего хозяйства, нормализация на стабильные гены^[1]

Методы нормализации

Масштабирование

Один из ДНК-микрочипов выбирается в качестве базового, затем все остальные масштабируются таким образом, чтобы их средняя интенсивность равнялась средней интенсивности базового (этот способ эквивалентен построению линейной регрессии каждого чипа на базовый и последующей нормализации при помощи регрессионной функции).

Для большей устойчивости можно использовать усечённое среднее. Так, в стандартном программном обеспечении производителя микрочипов Affymetrix перед подсчётом среднего отбрасываются по 2% наибольших и наименьших значений интенсивности. Другая модификация — масштабирование к средней интенсивности не по всему базовому чипу, а по каждому подмножеству его проб, соответствующих одному гену.

Affymetrix предлагает использовать масштабирование на последнем этапе предобработки, применяя его непосредственно к матрицам экспрессии, однако, возможно и применение к матрицам интенсивности.

Схема выполнения масштабирования

     Выбрать столбец  матрицы  в качестве базового.
     Вычислить (усечённое) среднее  по столбцу 
     Для всех остальных столбцов матрицы : вычислить (усечённое) среднее  по столбцу ; вычислить ; каждый элемент столбца  умножить на

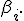
Нелинейные методы

Предложено большое количество нелинейных способов нормализации данных, использующих различные настраиваемые функции, заменяющие линейную регрессию из предыдущего примера. Среди таких функций cross-validated splines^[1], running median lines^[1], loess smoothers^[1], и т.д. В типичном случае нелинейная нормализация проводится по множеству рангово-инвариантных проб, то есть, проб, имеющих один и тот же ранг во всех микрочипах.

Схема выполнения нелинейной нормализации

     Выбрать столбец  матрицы  в качестве базового.
     Для всех столбцов  матрицы настроить параметры нелинейной функции , отображающей столбец  на столбец . Пусть  - полученное отображение.
     Нормализованные значения в столбце  определяются как

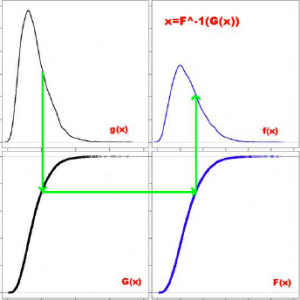
Метод квантильной нормализации преобразует распределения интенсивностей

Квантильная нормализация

Цель квантильной нормализации - сделать одинаковыми эмпирические распределения интенсивностей всех микрочипов. Для этого используется преобразование вида $x'_i=F^{-1}\left[G\left(x_i\right)\right],$ где $G$ - эмпирическое распределение интенсивностей каждого чипа, $F$ - эмпирическое распределение интенсивностей усреднённого чипа. Можно модифицировать метод, оценивая $F^{-1}$ и $G$ более гладкими функциями. Однако, для данных большой размерности на практике достаточно и грубой оценки.

Приводимый метод квантильной нормализации - не единственный способ нормализации, основанный на квантилях. Описан метод, основанный на построении сплайнов по множеству квантилей^[1], непараметрический метод присваивания одного и того же распределения каждому микрочипу^[1] и др.

Схема выполнения квантильной нормализации

     Имея  микрочипов размерности , построить матрицу  размерности , где в каждом столбце находятся значения интенсивности по каждому чипу.
     Отсортировать все столбцы  независимо друг от друга, сформировав матрицу 
     Взять среднее по каждой строке матрицы  и создать  - матрицу той же размерности, что и , в каждой строке которой все значения равны среднему по строке 
     Получить матрицу , переставив значения в столбцах  в том порядке, в каком они стояли в исходной матрице

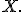
Циклическая нормализация при помощи локальной регрессии (cyclic loess)

Данный метод основан на многократном применении локальной регрессии (англ. LOWESS, LOESS) к парам ДНК-микрочипов. Процедура перебирает все попарные комбинации микрочипов, повторяя процесс нормализации до достижения сходимости. Одним из её недостатков является необходимость $O\left(n^2\right)$ применений локальной регресиии, хотя, обычно требуется всего один или два шага цикла.

Ниже приведён алгоритм циклической loess-нормализации. Индексы $i$ и $j$ соответствуют номерам микрочипов, а индекс $k$ - номеру пробы или подмножества проб, соответствующих одному гену.

Примечания

Это незавершённая статья. Вы поможете проекту, исправив и дополнив её.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9D%D0%BE%D1%80%D0%BC%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D1%8F_%D0%94%D0%9D%D0%9A-%D0%BC%D0%B8%D0%BA%D1%80%D0%BE%D1%87%D0%B8%D0%BF%D0%BE%D0%B2»

Категории: Биоинформатика | Незавершённые статьи

@@ Строка 43: / Строка 43: @@
       Получить матрицу <tex>X_n</tex>, переставив значения в столбцах <tex>X'_s</tex> в том порядке, в каком они стояли в исходной матрице <tex>X.</tex>
-=== Циклическая нормализация при помощи локальной регрессии ===
+=== Циклическая нормализация при помощи локальной регрессии (cyclic loess)===
-[[Алгоритм LOWESS]]
+Данный метод основан на многократном применении [[Алгоритм LOWESS|локальной регрессии]] (англ. LOWESS, LOESS) к парам ДНК-микрочипов. Процедура перебирает все попарные комбинации микрочипов, повторяя процесс нормализации до достижения сходимости. Одним из её недостатков является необходимость <tex>O\left(n^2\right)</tex> применений локальной регресиии, хотя, обычно требуется всего один или два шага цикла.
+Ниже приведён алгоритм циклической loess-нормализации. Индексы <tex>i</tex> и <tex>j</tex> соответствуют номерам микрочипов, а индекс <tex>k</tex> - номеру пробы или подмножества проб, соответствующих одному гену.
 == Примечания ==