Исследование скорости сходимости параметров и гиперпараметров (пример)
Материал из MachineLearning.
(→Вычислительный эксперимент) |
(→Вычислительный эксперимент) |
||
| Строка 76: | Строка 76: | ||
=Вычислительный эксперимент= | =Вычислительный эксперимент= | ||
| - | Эксперименты проводятся на 6 моделях, для каждой из которых рассматриваются 2 случая: (alpha variable) (alpha constant) | + | Эксперименты проводятся на 6 моделях, для каждой из которых рассматриваются 2 случая: <tex>A^{-1}=diag(\mathbf{\alpha})</tex> (alpha variable) и <tex>A^{-1}=\alpha I_W</tex> (alpha constant). |
| - | + | Для каждого случая проводится настройка модели по описанному алгоритму. Затем строятся графики изменения параметров и гиперпараметров по шагам алгоритма (величины параметров и гиперпараметров нормированы). | |
| - | + | '''Рассматриваемые модели''': | |
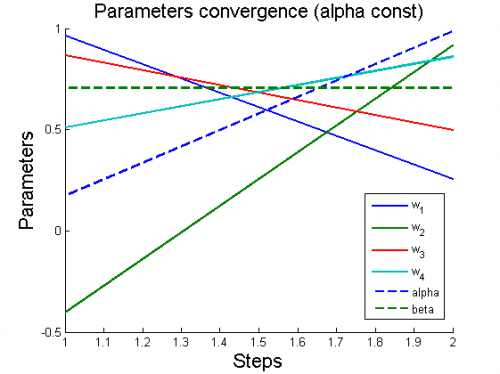
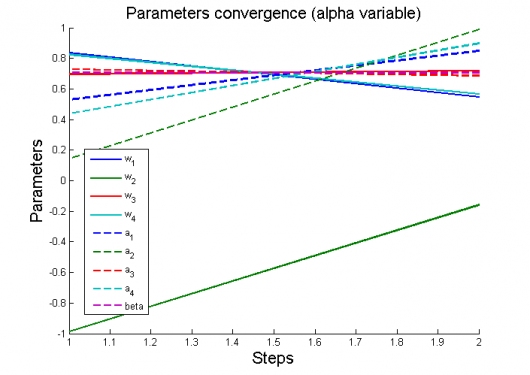
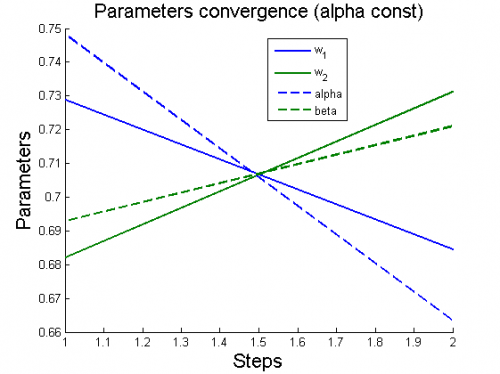
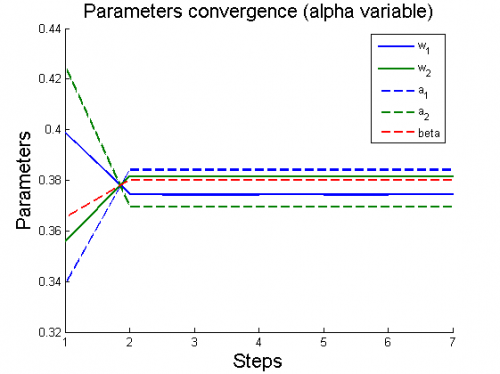
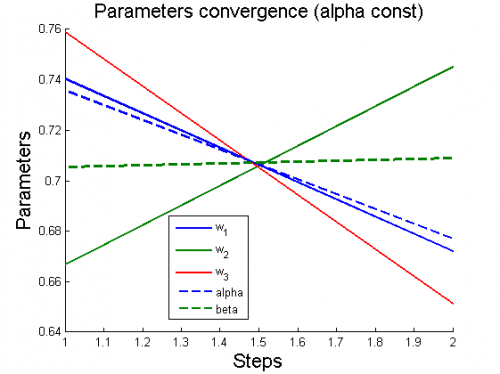
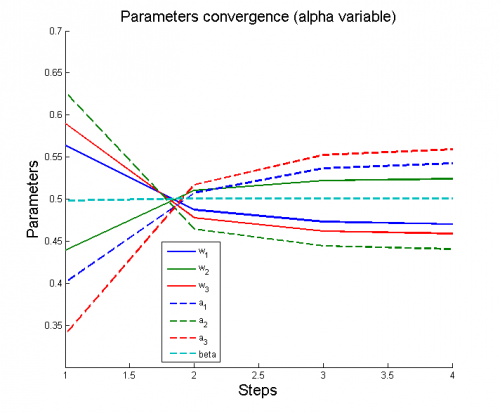
| - | + | 1) модель полиномиальной регрессии <tex>y=\sum_{i=1}^4 w_i x^{i-1}</tex> | |
| - | + | [[Изображение:1ParamConvergence(AlphaConst).png|border|500x420px]] | |
| + | [[Изображение:1ParamConvergence(AlphaVariable).png|border|530x500px]] | ||
| - | 5) модель трехпараметрического распределения Вейбулла <tex>y= | + | |
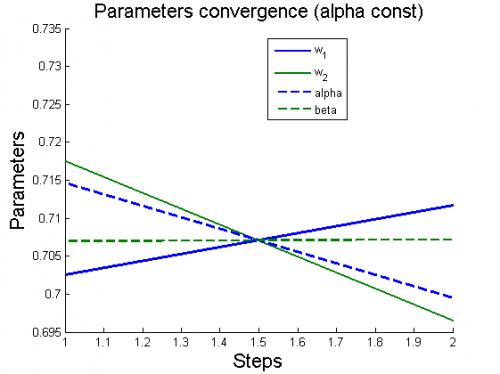
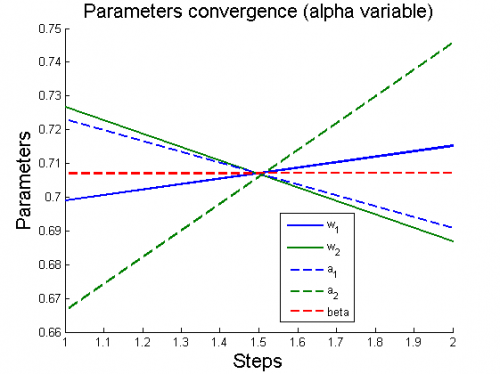
| + | 2) модель <tex>y = w_1 + w_2\, ln x</tex> | ||
| + | |||
| + | [[Изображение:2ParamConvergence(AlphaConst).png|border|500x420px]] | ||
| + | [[Изображение:2ParamConvergence(AlphaVariable).png|border|500x420px]] | ||
| + | |||
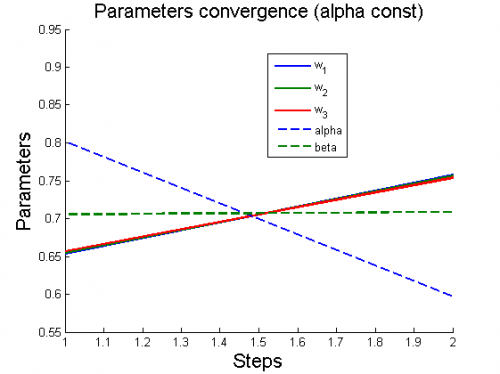
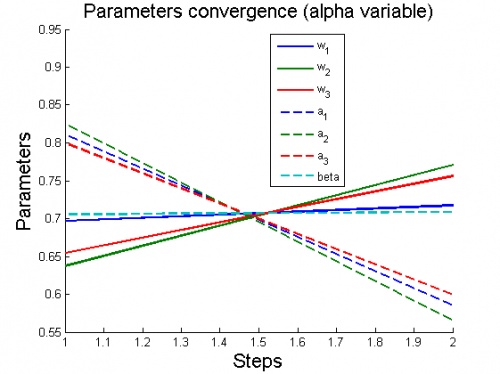
| + | 3) модель <tex>y = w_1 + \frac{w_2}{x}</tex> | ||
| + | |||
| + | [[Изображение:3ParamConvergence(AlphaConst).png|border|500x420px]] | ||
| + | [[Изображение:3ParamConvergence(AlphaVariable).png|border|500x420px]] | ||
| + | |||
| + | 4) модель <tex>y = w_1 + w_2\, e^{-w_3x}</tex> | ||
| + | |||
| + | [[Изображение:4ParamConvergence(AlphaConst).png|border|500x420px]] | ||
| + | [[Изображение:4ParamConvergence(AlphaVariable).png|border|500x420px]] | ||
| + | |||
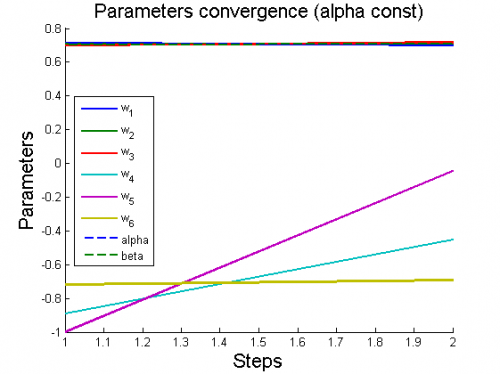
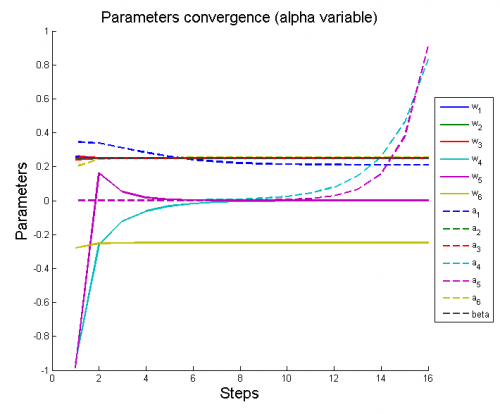
| + | 5) модель трехпараметрического распределения Вейбулла <tex>y=w_1 w_2 x^{w_2-1}\exp(-w_1(x-w_3)^{w_2})</tex> | ||
| + | |||
| + | [[Изображение:5ParamConvergence(AlphaConst).png|border|500x420px]] | ||
| + | [[Изображение:5ParamConvergence(AlphaVariable).png|border|500x420px]] | ||
6) модель с тригонометрическими функциями <tex>y=a_0+\sum_{i=1}^n\bigl(a_i\cos(i\omega{x})+b_i\sin(i\omega{x})\bigr)</tex> | 6) модель с тригонометрическими функциями <tex>y=a_0+\sum_{i=1}^n\bigl(a_i\cos(i\omega{x})+b_i\sin(i\omega{x})\bigr)</tex> | ||
| + | |||
| + | [[Изображение:6ParamConvergence(AlphaConst).png|border|500x420px]] | ||
| + | [[Изображение:6ParamConvergence(AlphaVariable).png|border|500x420px]] | ||
Версия 21:29, 22 декабря 2010
|
Для фиксированной регрессионной модели исследуется скорость сходимости параметров и гиперпараметров при ее настройке через двухуровневый байесовский вывод.
Постановка задачи
Рассмотрим следующую модель регрессии, описывающую связь между свободной и зависимой переменными:
Пусть случайная величина имеет нормальное распределение
. При этом будем обозначать
.
Вектор называется параметрами модели и рассматривается как многомерная случайная величина. Пусть плотность распределения параметров имеет вид многомерного нормального распределения
с матрицей ковариации
. В данном примере будут рассматриваться 2 случая:
, где
- число параметров модели, и
, где
- единичная матрица размерности
.
Величины и
называются гиперпараметрами модели.
Для нескольких фиксированных функций , задающих модель, через двухуровневый байесовский вывод происходит настройка параметров и гиперпараметров. Требуется проанализировать изменение параметров и гиперпараметров по мере настройки.
Алгоритм настройки регрессионной модели (двухуровневый байесовский вывод)
Настройка модели происходит через двухуровневый байесовский вывод.
Описание метода
Т.к. , то для фиксированной модели f плотность вероятности появления данных
где
Т.к. , то
где
Тогда, если обозначить , то
Таким образом, минимизация по
дает максимум априорной плотности распределения параметров
на выборке
. Минимизация осуществляется алгоритмом Левенберга-Марквардта.
Считая, что в точке минимума функционал
представим в виде:
получаем, что логарифм функции правдоподобия равен
Гиперпараметры и
находятся итерационно из условия максимизации полученной функции правдоподобия:
При
, где
- собственные числа матрицы
- части Гессиана, не зависящей от
.
, где
При
, где
, где
Алгоритм
1) Задаем начальные значения ,
и
2) Ищем локальный минимум функции ошибки по
3) Ищем локальный максимум функции правдоподобия гиперпараметров по
4) Повторяем шаги 2 и 3 до сходимости функционала
Вычислительный эксперимент
Эксперименты проводятся на 6 моделях, для каждой из которых рассматриваются 2 случая: (alpha variable) и
(alpha constant).
Для каждого случая проводится настройка модели по описанному алгоритму. Затем строятся графики изменения параметров и гиперпараметров по шагам алгоритма (величины параметров и гиперпараметров нормированы).
Рассматриваемые модели:
1) модель полиномиальной регрессии
2) модель
3) модель
4) модель
5) модель трехпараметрического распределения Вейбулла
6) модель с тригонометрическими функциями