Контроль качества в анализе ДНК-микрочипов
Материал из MachineLearning.
| Строка 32: | Строка 32: | ||
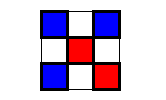
[[Изображение:checkering_board.png|thumb|300px|9 квадратов 3×3. Красным и розовым помечены пробы с интенсивностью больше среднего. Красные - пробы на диагоналях, розовые - вне диагоналей. Квадраты, у которых такое же распределение красного цвета, что и у центрального, обведены розовым.]] | [[Изображение:checkering_board.png|thumb|300px|9 квадратов 3×3. Красным и розовым помечены пробы с интенсивностью больше среднего. Красные - пробы на диагоналях, розовые - вне диагоналей. Квадраты, у которых такое же распределение красного цвета, что и у центрального, обведены розовым.]] | ||
Основное предположение алгоритма Лэнгдона<ref name="Langdon">W.B.Langdon et al. A Survey of Spatial Defects in | Основное предположение алгоритма Лэнгдона<ref name="Langdon">W.B.Langdon et al. A Survey of Spatial Defects in | ||
| - | Homo Sapiens Affymetrix GeneChips: http://www.cs.ucl.ac.uk/staff/w.langdon/ftp/papers/langdon_tcbb.pdf </ref> - для идеального чипа значения интенсивностей смежных проб статистически независимы. Поэтому поиск дефектов на чипе сводится к поиску областей, где значения интенсивностей либо всегда больше, либо всегда меньше средних интенсивностей для данной области. Для поиска таких областей на матрицу интенсивностей проб накладывается сетка, состоящая из квадратов 3×3. Каждый данный квадрат состоит соответственно из 9 квадратиков, представляющих собой пробы. Если значения интенсивностей нормализованы, то вероятность того, что интенсивность в заданном квадратике больше или меньше среднего значения равна <tex>\frac{1}{2}</tex>. Для соблюдения статистической независимости исследуются пробы, расположенные на диагоналях квадрата. Если в данной области нет дефектов, то | + | Homo Sapiens Affymetrix GeneChips: http://www.cs.ucl.ac.uk/staff/w.langdon/ftp/papers/langdon_tcbb.pdf </ref> - для идеального чипа значения интенсивностей смежных проб статистически независимы. Поэтому поиск дефектов на чипе сводится к поиску областей, где значения интенсивностей либо всегда больше, либо всегда меньше средних интенсивностей для данной области. Для поиска таких областей на матрицу интенсивностей проб накладывается сетка, состоящая из квадратов 3×3. Каждый данный квадрат состоит соответственно из 9 квадратиков, представляющих собой пробы. Если значения интенсивностей нормализованы, то вероятность того, что интенсивность в заданном квадратике больше или меньше среднего значения равна <tex>\frac{1}{2}</tex>. Для соблюдения статистической независимости исследуются пробы, расположенные на диагоналях квадрата. Если в данной области нет дефектов, то интенсивности проб на диагоналях с одинаковой вероятностью могут быть больше или меньше среднего значения. Назовем квадрат, интенсивности всех 4 диагональных проб одновременно больше или меньше среднего, "подозрительным". Вероятность этого равна <tex>\frac{1}{16}</tex>. Каждый квадрат 3×3 окружен 8 такими же квадратами. В отсутствии дефектов вероятность того, что один из соседних квадратов имеет 5 квадратиков, у которых интенсивности также либо больше, либо меньше среднего значения равна <tex>\frac{1}{32}</tex>. Отсюда, вероятность того, что проба находится в центре "подозрительного" квадрата, имеющего ровно <tex>m</tex> "подозрительных" соседей равна |
::<tex>\frac{1}{16}*C_8^m*(\frac{1}{32})^m*(\frac{31}{32})^{8-m}</tex>. | ::<tex>\frac{1}{16}*C_8^m*(\frac{1}{32})^m*(\frac{31}{32})^{8-m}</tex>. | ||
Для значения <tex>m \ge 3</tex> это значения меньше 0.01. | Для значения <tex>m \ge 3</tex> это значения меньше 0.01. | ||
Версия 06:41, 3 ноября 2011
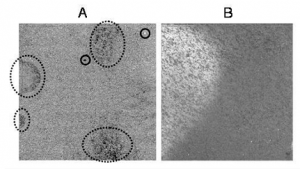
Важным этапом анализа ДНК-микрочипов является контроль качества изображений, полученных при сканировании чипов. На изображениях чипов могут появляться различные "пятна" или неоднородности, вызванные, например, пылью или неравномерным распределением свечения. Такие "пятна" достаточно трудно разглядеть невооруженным глазом на микрочипе в силу большого разброса значений интенсивностей свечения проб. Их обнаружения можно добиться путем сравнения интенсивности свечения пробы с каким-нибудь контрольным значением или с помощью моделирования значений в некотором наборе микрочипов.
Содержание |
Выбор контрольных значений
Важным вопросом является определение того, что считать выбросом или нетипичностью. Значение интенсивности выбросов не должно встречаться слишком редко, так это может быть обусловлено случайным распределением интенсивностей, а должно встречаться относительно часто вследствие некой достаточно заметной неоднородности. Необходимо найти способ определения выбросов с высокой чувствительностью и с высокой специфичностью. Для увеличения специфичности всегда можно использовать второй проход, в котором выбросы, окруженные пикселями, не являющимися выбросами, перестают считаться выбросами. Это основано на том, что выбросы представляют собой не отдельно взятые пробы, а некоторые области на чипе с нетипичным поведением. При исследовании технических репликат контрольным значением может быть выбрано медианное значение интенсивности пробы по всем репликатам, как это сделано в алгоритме Harshlight. Также контрольное значение может быть оценено по большой выборке чипов одного типа, например, средним, медианой или другими более устойчивыми способами.
Алгоритмы нахождения нетипичностей
Harshlight
Harshlight[1] — это программа, распространяемая в свободном доступе, предназначенная для поиска на изображении чипа нетипичностей трех видов: сильные дефекты ("extended defects"), компактные дефекты ("compact defects") и диффузные дефекты ("diffuse defects"). Сильные дефекты — это большие области на изображении чипа, которые сильно отличаются от остального части чипа по интенсивности свечения. Компактные дефекты — области небольшого размера либо слишком ярких, либо слишком темных проб. Диффузные дефекты — области чипа, плотности распределения ярких или темных проб в которых значительно отличаются от их плотности в остальной части чипа. Сначала алгоритм ищет сильные дефекты, а затем компактные и диффузные дефекты. При обнаружении сильных дефектов авторы алгоритма настоятельно рекомендуют исключить чип из исследования.
Алгоритм начинает работу с построения изображения ошибок ("error image") , которое представляет собой отклонение логарифмированных интенсивностей конкретного чипа от других в эксперименте. Это изображение представляется в виде
,
где — фон изображения
,
— локальные вариации, которые при отсутствии дефектов вызваны представляющими основной интерес изменениями экспрессии генов. Предположив, что фон и локальные вариации являются некоррелированными величинами, можно записать
.
Для оценки используется изображение
, полученное из
путем медианной фильтрации. Далее считается
. Если оно превышает заданный порог, то считается, что сильный дефект обнаружен.
Для обнаружения компактных дефектов применяется следующий подход: мы строим бинарные изображения по изображению , в котором 1 соответствуют пиксели, с интенсивностью, либо меньшей
-перцентили (темные выбросы), либо большей
-перцентили (яркие выбросы). Для этих двух изображений применяется алгоритм нахождения связанных областей FloodFill. Если размер обнаруженного связной области превышает заданного порога, то считается, что обнаружен компактный дефект.
Для обнаружения диффузных дефектов опять определяются темные и яркие выбросы. Темным выбросом считается пиксель с интенсивностью , светлым —
, где
— некоторый процент от ожидаемого значения интенсивности. Изображения темных и ярких выбросов сканируются окном, и определяется локальная плотность выбросов в области внутри этого окна. Далее ко всему изображению применяется процедура замыкания[1] для более точного определения области диффузного дефекта. Обнаруженные дефекты заполняются либо пропусками, либо медианой по остальным чипам в эксперименте.
MBR
Microarray Blob Remover[1] (MBR) —программа, распространяемая в свободном доступе, предназначенная для поиска на изображении чипов так называемых "блобов". "Блоб" —большая связная область пикселей с высокой интенсивностью свечения, возникшая в результате внешних источников и не связанная с уровнем транскрипции.
Алгоритм MBR состоит из двух шагов. На первом шаге изображение сканируется квадратным окном 100×100. Окно двигается по вертикали и горизонтали на 50 проб. В каждом окне считается количество проб, интенсивность которых больше k-ой квантили, по умолчанию k выбирается равным 90. Если количество таких проб в окне превышает 50% от общего числа проб в окне, то выполняется следующий шаг. Квадратное окно сканируется круглым, с радиусом 20. Если процент проб в этом окне, интенсивность которых больше (k-5)-ой квантили, превышает p%, то все пробы внутри окошка объявляются принадлежащим "блобу". По умолчанию p равно 90.
MBR обнаруживает "блобы", но не исправляет дефекты сам. Пробы, принадлежащие найденным "блобам" MBR записывает в .CEL файл на место секции "Outlier entries", полученной при рaботе Affymetrix GCOS.
Алгоритм Лэнгдона
Основное предположение алгоритма Лэнгдона[1] - для идеального чипа значения интенсивностей смежных проб статистически независимы. Поэтому поиск дефектов на чипе сводится к поиску областей, где значения интенсивностей либо всегда больше, либо всегда меньше средних интенсивностей для данной области. Для поиска таких областей на матрицу интенсивностей проб накладывается сетка, состоящая из квадратов 3×3. Каждый данный квадрат состоит соответственно из 9 квадратиков, представляющих собой пробы. Если значения интенсивностей нормализованы, то вероятность того, что интенсивность в заданном квадратике больше или меньше среднего значения равна . Для соблюдения статистической независимости исследуются пробы, расположенные на диагоналях квадрата. Если в данной области нет дефектов, то интенсивности проб на диагоналях с одинаковой вероятностью могут быть больше или меньше среднего значения. Назовем квадрат, интенсивности всех 4 диагональных проб одновременно больше или меньше среднего, "подозрительным". Вероятность этого равна
. Каждый квадрат 3×3 окружен 8 такими же квадратами. В отсутствии дефектов вероятность того, что один из соседних квадратов имеет 5 квадратиков, у которых интенсивности также либо больше, либо меньше среднего значения равна
. Отсюда, вероятность того, что проба находится в центре "подозрительного" квадрата, имеющего ровно
"подозрительных" соседей равна
.
Для значения это значения меньше 0.01.
Для нахождения среднего значения интенсивностей проб на чипе Лэнгдон использует следующий подход. Берется большая выборка чипов одного типа. Ищется среднее значение логарифма интенсивности пробы в определенном месте на чипе. При этом отбрасываются из рассмотрения 0.5% самых больших и 0.5% самых маленьких значений интенсивностей, то есть среднее берется по оставшимся 99% значений. Для нормализации интенсивностей проб используется квантильная нормализация по строкам[1].
SmudgeMiner
SmudgeMiner[1] строит по большой выборке чипов одного типа "стандартный чип". Логарифмы интенсивности проб "стандартного чипа" - это 20% урезанное среднее логарифмов интенсивностей проб, находящихся в том же месте, по всем чипам. SmudgeMiner строит график разности логарифмов интенсивности исследуемого чипа и "стандартного чипа"
,
где - индекс по пробам,
- индекс по чипам,
- индекс всех чипов. Для оценки локального фона используется следующее значение:
,
где - 20% урезанное среднее по значениям
, удовлетворяющих условию
.
- интенсивность пробы
на чипе
,
- логарифм интенсивности пробы
на "стандартном чипе", а
-
-ая квантиль значений
. Для оценки фактора шкалирования используется следующее значение:
.
По значениям для всех проб на чипе строятся картинки распределения значений локального фона и фактора шкалирования по чипу. Для нахождения дефектов используется следующее значение:
,
где - разница между логарифмом интенсивности пробы в строке
и столбце
и логарифмом среднего значения интенсивности пробы по всем чипам.
- корреляция Пирсона между
и
по всем значениям
и
. Для чипов без дефектов значение
должно быть равным 0, а для чипов с дефектами