Статистический отчет при создании моделей

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Вычислительный эксперимент)
(→Вычислительный эксперимент)
Строка 80: Строка 80:
Отчет, построенный программой:
Отчет, построенный программой:
-
<matlab>
+
<code>
Статистический анализ линейной модели
Статистический анализ линейной модели
Строка 104: Строка 104:
Коэффициент множественной корреляции равен 3.8029
Коэффициент множественной корреляции равен 3.8029
-
</matlab>
+
</code>
=== Модель №2 ===
=== Модель №2 ===

Версия 21:17, 14 ноября 2011

Содержание

В данной работе приведен обзор статистических методов оценивания качества регрессионных моделей, используемых популярными программами машинного обучения и статистической обработки данных. Приведены примеры вычисления и анализа полученных оценок.

Постановка задачи

Имеется пространство объектов-строк \mathbb{X} = \mathbb{R}^n и пространство ответов \mathbb{Y} = \mathbb{R}. Задана выборка (x_i,\ y_i)_{i=1}^l \in \mathbb{X} \times \mathbb{Y}. Обозначеним:

  • X = \(x_1 <br> \ \vdots\ <br> x_l\)  — матрица информации или матрица плана;
  • w = \(w_1<br> \ \vdots <br> w_n\)  — вектор параметров;
  • y = \(y_1<br>\ \vdots<br>y_l\)  — целевой вектор.

Будем считать, что зависимость имеет вид

y(x) = f(x) + \varepsilon(x),

где f(x)  — некоторая неслучайная функция, \varepsilon(x)  — случайная величина, с нулевым математически ожиданием. В моделях многомерной линейной регрессии предполагается, что неслучайная составляющая имеет вид:

f(x) = <w, \ x> .

Требуется численно оценить качество модели при заданном векторе параметров w.

Описание решения

Предполагая, что матрица ковариации вектора ошибки \varepsilon = \(\varepsilon_1 <br> \ \vdots\ <br> \varepsilon_l\) имеет вид \sigma^2 V , где V = diag (v_1, \dots, v_l) , получаем выражение для оценки параметров w взвешенным методом наименьших квадратов:

\hat w = (X^T V^{-1} X)^{-1} X^T V^{-1} y. Основными инструментами оценки качества линейной модели является анализ:

В работе рассматривается

  • анализ регрессионных остатков, включающий в себя:
    • вычисление среднеквадратичной ошибки:

\mathbb{MSE} = \sum_{i=1}^l \left(y_i - f\left(x_i\right)\right)^2;

    • вычисление коэффициента детерминации:

\mathbb{R}^2 = 1 - \frac{\sum_{i=1}^l \left(y_i - f\left(x_i\right)\right)^2}{\sum_{i=1}^l \left(y_i - \bar y\right)^2}, где \bar y = \frac{1}{l} \sum_{i=1}^l y_i;

    • проверку гипотезы о равенстве нулю математического ожидания регрессионных остатков на основе критерия знаков;
    • проверку гипотезы о равенстве дисперсий (пропорциональности с заданными коэффициентами) регрессионных остатков на основе критерия Ансари-Брэдли;
    • проверку гипотезы о нормальности распределения регрессионных остатков на основе критерия хи-квадрат и критерия Жарка-Бера;
  • вычисление расстояния Махаланобиса и Кука;
  • вычисление корреляций признаков, корреляций признаков и значений моделируемой функции и коэффициента множественной регрессии.

Вычислительный эксперимент

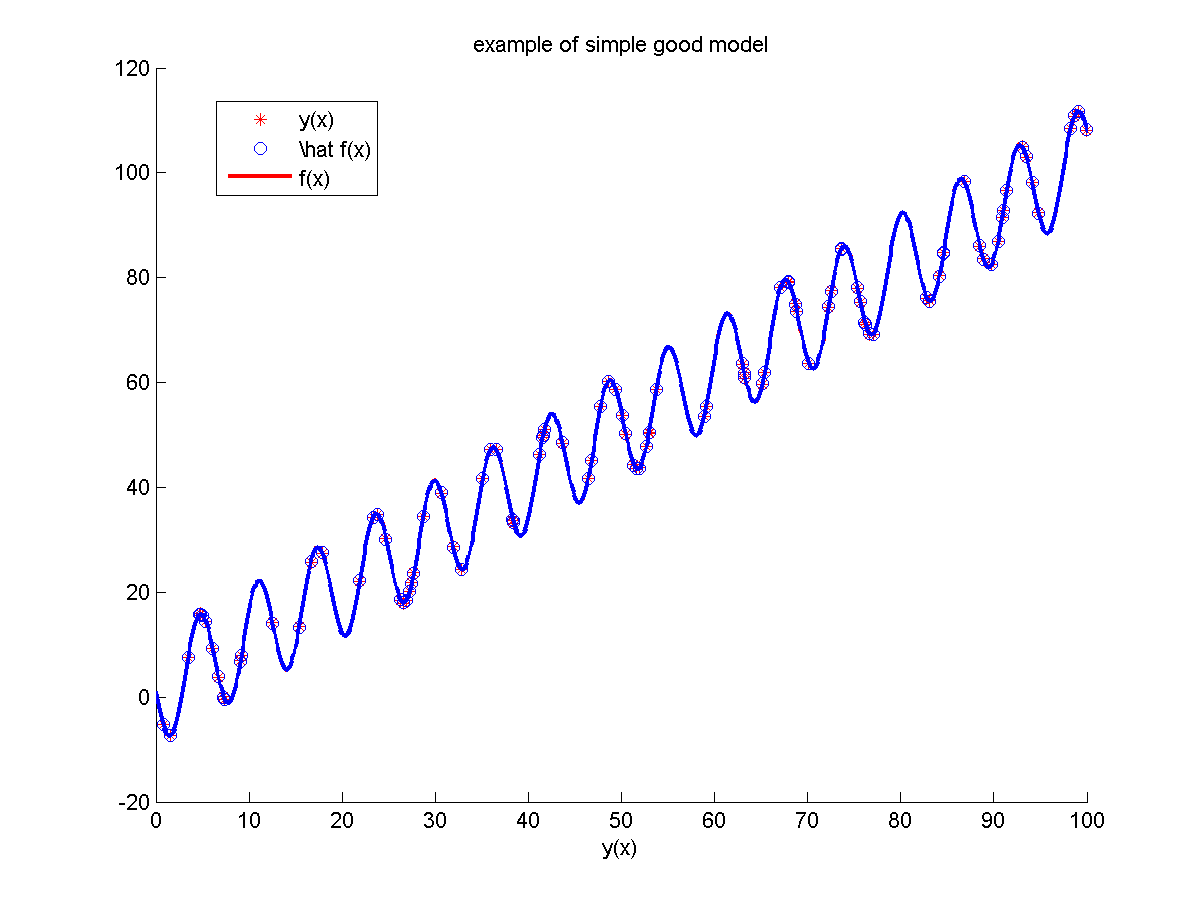
В данном отчете представлены результаты применения созданного инструмента для анализа модели. Отчет состоит из трех экспериментов, демонстрирующих работу инструмента на различных по качеству моделях.

Вставляйте сюда неотформатированный текст.=== Модель №1 ===

Неизвестная зависимость: y(x) = x - 10 \sin(x) + \exp(x / 100).

Для построения модели использовалось 100 объектов независимо равномерно распределительных на отрезке [0, 100]. В качестве шума использовались независимые случайные величины из распределения N(0, \; 0,1). В качестве признаков использовались x, \; \sin(x), \;\exp(x / 100). Параметры модели подбирались с помощью метода наименьших квадратов.

image:statModelAnalisys1.png

Отчет, построенный программой:

Статистический анализ линейной модели

Среднеквадратичная ошибка: 0.009639 Значение коэффициента детерминации R^2: 0.99999 Расстояние Кука: 1.0086 (соотношение между дисперсиями признаков не заданы пользователем) Расстояние Махаланобиса: 3.1018 (соотношение между дисперсиями признаков не заданы пользователем)

Гипотезу о равенстве нулю математического ожидания регрессионных остатков нельзя отвергнуть при уровне значимости 0.05. Для анализа использован критерий знаков. Значение статистики попало в 0.76418-хвост распределения. Гипотеза о равенстве дисперсий регрессионных остатков отвергнута при уровне значимости 0.05. Для анализа использован критерий Ансари-Брэдли. Значение статистики попало в 0.5466-хвост распределения. Гипотеза о нормальности распределения регрессионных остатков отвергнута при уровне значимости 0.05. Для анализа использован критерий хи-квадрат. Значение статистики попало в 0.05685-хвост распределения. Гипотеза о нормальности распределения регрессионных остатков отвергнута при уровне значимости 0.05. Для анализа использован критерий Жарка-Бера. Значение статистики попало в 0.5-хвост распределения.

Матрица корреляции признаков: 

      1    0.010935     0.99136

0.010935 1 -0.0061593 

0.99136  -0.0061593           1

Вектор корреляции признаков и значений функции: 

0.97338

-0.21851 

0.96916

Коэффициент множественной корреляции равен 3.8029

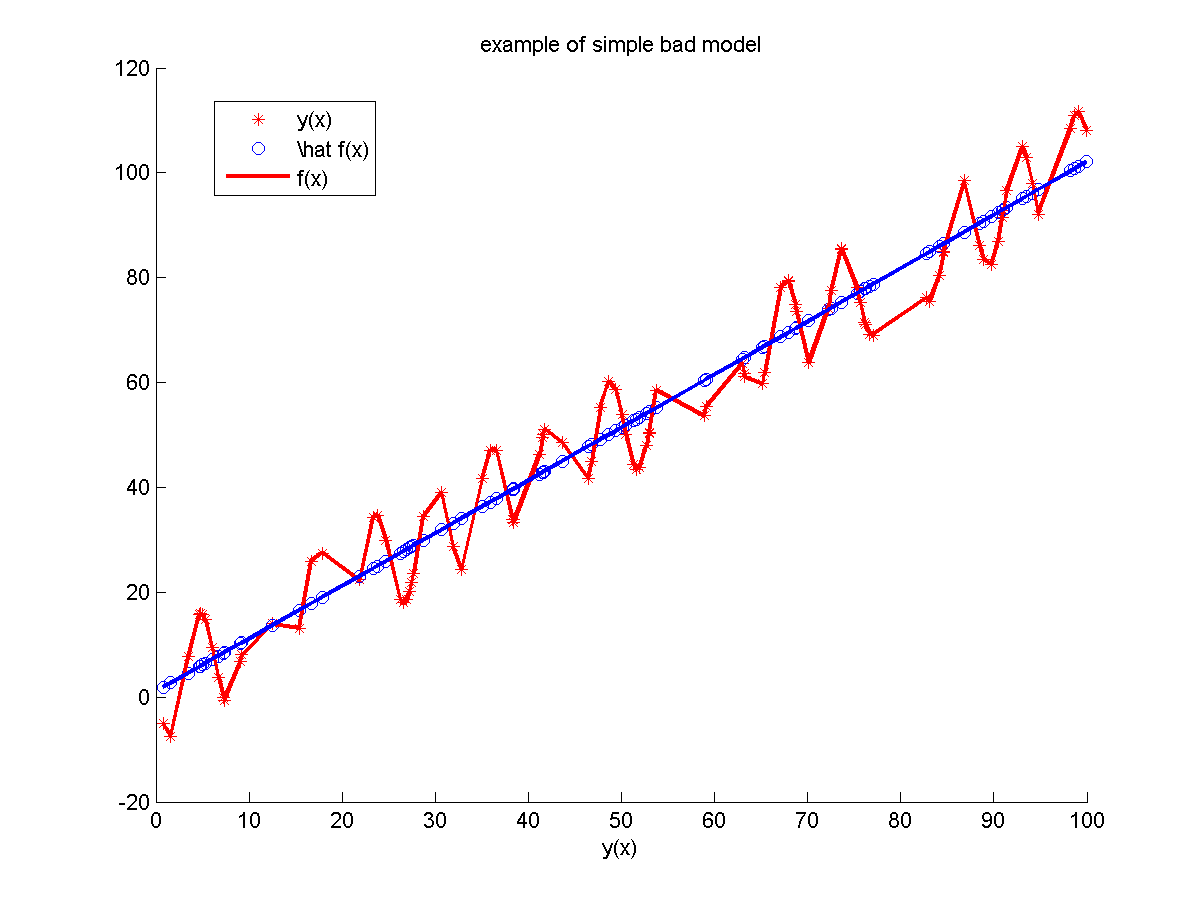
Модель №2

Неизвестная зависимость: y(x) = x - 10 \sin(x) + \exp(x / 100).

Для построения модели использовалось 100 объектов независимо равномерно распределительных на отрезке [0, 100]. В качестве шума использовались независимые случайные величины из распределения N(0, \; 0,1). В качестве признаков использовались x, \;\exp(x / 100). Параметры модели подбирались с помощью метода наименьших квадратов.

image:statModelAnalisys2.png

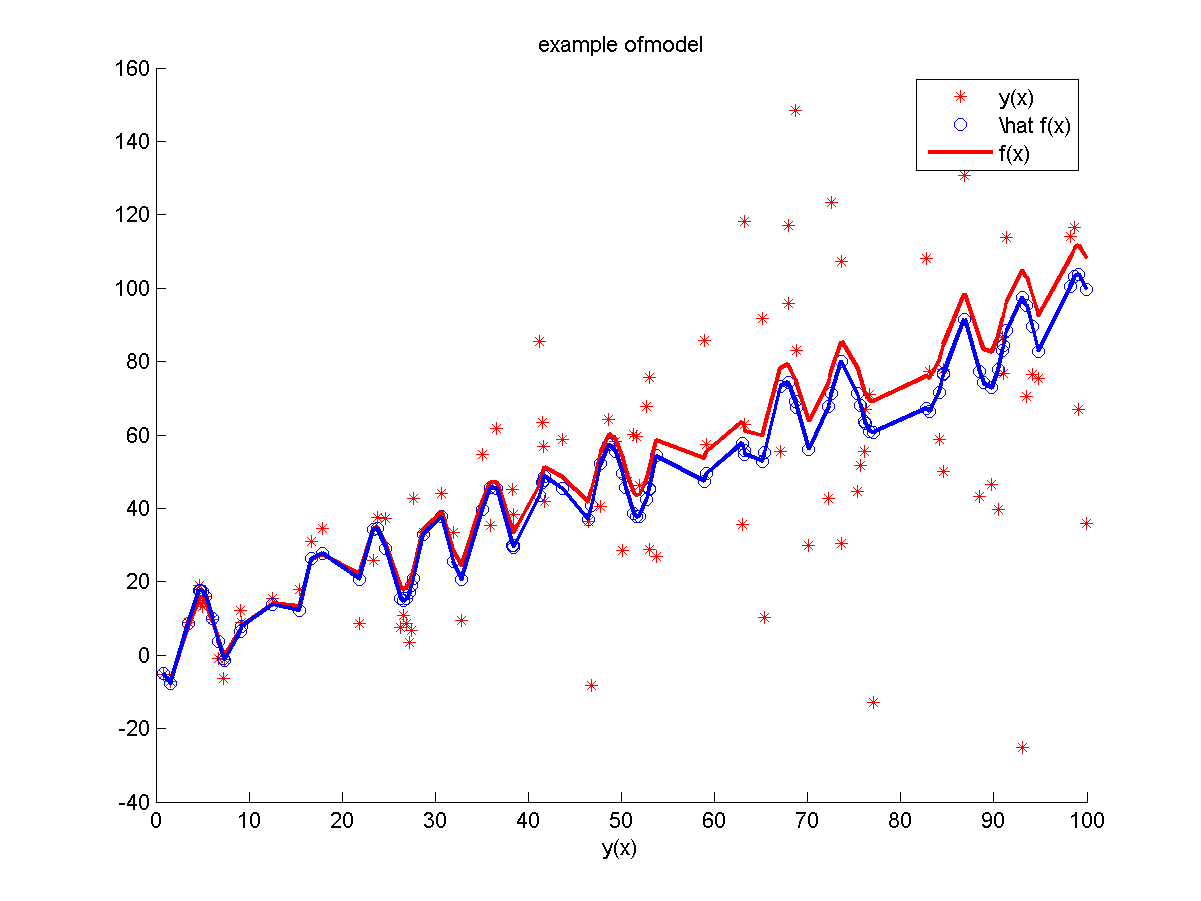
Модель №3

Неизвестная зависимость: y(x) = x - 10 \sin(x) + \exp(x / 100).

Для построения модели использовалось 100 объектов независимо равномерно распределительных на отрезке [0, 100]. В качестве шума использовались независимые случайные величины из распределения N(0, \; x). В качестве признаков использовались y(x) = x - 10 \sin(x) + \exp(x / 100). Параметры модели подбирались с помощью метода наименьших квадратов.

image:statModelAnalisys3.png

Исходный код и полный текст работы

Смотри также

Литература

Данная статья является непроверенным учебным заданием.
Студент: Юрий Янович
Преподаватель: В.В. Стрижов
Срок: 28 мая 2009

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BE%D1%82%D1%87%D0%B5%D1%82_%D0%BF%D1%80%D0%B8_%D1%81%D0%BE%D0%B7%D0%B4%D0%B0%D0%BD%D0%B8%D0%B8_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B5%D0%B9»
Личные инструменты