|
|
| Строка 120: |
Строка 120: |
| | *[http://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5 Биномиальное распределение] (Википедия) | | *[http://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5 Биномиальное распределение] (Википедия) |
| | *[http://en.wikipedia.org/wiki/Binomial_distribution Binomial distribution] (Wikipedia) | | *[http://en.wikipedia.org/wiki/Binomial_distribution Binomial distribution] (Wikipedia) |
| - |
| |
| - |
| |
| - |
| |
| - | == Интерпретация 21-го века ==
| |
| - |
| |
| - | {|border=1 align="center"
| |
| - | |+Таблица 1 – Характеристики биномиального распределения интерпретации 21-го века
| |
| - | | Пространство элементарных событий
| |
| - | | <tex>\sum_{i=1}^2\Omega_i(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})</tex>
| |
| - | |-
| |
| - | |Вероятность
| |
| - | |<tex>\prod_{i=1}^2P(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=\frac{n!}{n_1! n_2!}p_1^{n_1}p_2^{n_2}</tex>
| |
| - | |-
| |
| - | | Максимальная вероятность
| |
| - |
| |
| - | (при математическом ожидании
| |
| - |
| |
| - | распределения)
| |
| - |
| |
| - | |<tex> \left(\frac{n!}{n_i!n_2!}p_1^{n_1}p_2^{n_2}\right)_{max}= \frac{1}{2}</tex>
| |
| - | |-
| |
| - | | Математическое ожидание
| |
| - |
| |
| - | (как максимальное произведение
| |
| - |
| |
| - | математических ожиданий
| |
| - |
| |
| - | случайных величин)
| |
| - | |<tex>\left(\prod_{i=1}^2E(t_i, X_i=n_i \mid t_{i-1},X_{i-1})\right)_{max}=\frac{1}{2}</tex>
| |
| - | |-
| |
| - | | Дисперсия
| |
| - | |<tex>\sum_{i=1}^2D(t_i,X_i \mid t_{i-1},X_{i-1})=\sum_{i=1}^2(n-n_{i-1})p_iq_i</tex>
| |
| - | |-
| |
| - | | Максимальная дисперсия
| |
| - |
| |
| - | (при математическом ожидании
| |
| - |
| |
| - | распределения)
| |
| - |
| |
| - | |<tex>D(X_1,X_2|X_1)_{max}=\left(\sum_{i-1}^2(n-n_{i-1})p_iq_i \right)_{max}=\frac{3}{4}</tex>
| |
| - | |-
| |
| - | |Ковариационная матрица
| |
| - | |<tex>B=\| b_{ij} \|</tex>, где :<tex>\rho _{ij} = \begin{cases} 1, & i=j,\\0, & i \not= j\end{cases} </tex>
| |
| - | |-
| |
| - | |Корреляционная матрица
| |
| - | |<tex>P=\| \rho_{ij} \|</tex>, где
| |
| - | :<tex>\rho_{ij} = \begin{cases} 1, & i=j,\\0, & i \not= j\end{cases}</tex>
| |
| - | |-
| |
| - | |<tex>\chi^2</tex> - критерий
| |
| - | |<tex> \chi^2=\sum_{i=1}^2 [X_i-(n -n_{i-1})p_i^{(0)}]^2/(n -n_{i-1})p_i^{(0)}=</tex>
| |
| - | <tex>=-n+\sum_{i=1}^2X_i^2 /(n-n_{i-1})p_i^{(0)}</tex>
| |
| - | |}
| |
| - |
| |
| - | ==Биномиальная схема повторных циклов случайных зависимых экспериментов==
| |
| - |
| |
| - | Каждый цикл экспериментов осуществляют '''методом выбора без возвращения''' в дискретной временной последовательности
| |
| - |
| |
| - | ::<tex>t_1, t_2.</tex>
| |
| - |
| |
| - | Каждая из случайных величин распределения
| |
| - |
| |
| - |
| |
| - | ::<tex>X_i=n_i \mid X_{i-1}=n_{i-1}</tex>
| |
| - |
| |
| - | это <tex>n_i</tex> наступлений одного события
| |
| - |
| |
| - | ::<tex>x_i, i =1,2</tex>
| |
| - |
| |
| - | в <tex>i</tex> - ый момент времени при условии, что в <tex>(i-1)</tex> - ый момент произошло <tex>n_{i-1}</tex> наступлений предшествующего события <tex>x_{i-1}</tex>, —
| |
| - | [[ распределение Бернулли | распределения Бернулли]] с успехом, вероятности которых <tex>p_i</tex> нормированы
| |
| - |
| |
| - | ::<tex>p_1+p_2=1</tex>
| |
| - |
| |
| - | и неизменны во время проведения экспериментов.
| |
| - |
| |
| - | Если в каждом цикле экспериментов вероятность наступления события <tex>x_i</tex> равна <tex>p_i</tex>, то биномиальная вероятность равна вероятности того, что при <tex>n</tex> экспериментах события <tex>x_1, x_2</tex> наступят <tex>n_1, n_2</tex> раз соответственно.
| |
| - |
| |
| - | '''Случайная величина биномиального распределения''' в соответствующей точке дискретной временной последовательности <tex>t_1, t_2</tex> имеет:
| |
| - |
| |
| - | пространство элементарных событий
| |
| - |
| |
| - | ::<tex>\Omega_i(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})= [0\le n_i \le n-n_{i-1}], </tex>
| |
| - |
| |
| - | вероятность
| |
| - |
| |
| - | ::<tex>P(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})={n-n_{i-1}\choose n_i}p_i^{n_i},</tex>
| |
| - |
| |
| - | математическое ожидание
| |
| - |
| |
| - | ::<tex>E(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=( n-n_{i-1})p_i</tex>
| |
| - |
| |
| - | и дисперсию
| |
| - |
| |
| - | ::<tex>D(t_i,X_i \mid t_{i-},X_{i-1})=( n -n_{i-1})p_iq_i, \quad q_i=1-p_i .</tex>
| |
| - |
| |
| - | '''Пространство элементарных событий биномиального распределения''' есть сумма точечных пространств элементарных событий его случайных величин, образующих дискретную последовательность точек <tex> t_1, t_2 </tex> цикла, а ''вероятность биномиального распределения'' — произведение вероятностей его случайных величин.
| |
| - |
| |
| - | ==Биномиальное распределение — совместное распределение '''двух''' случайных величин <ref> http://ru.wikiznanie.org/wiki/ Биномиальное распределение, Настоящая интерпретация 21-го века. </ref>==
| |
| - |
| |
| - | ::<tex>\prod_{i=1}^2P(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=\frac{n!}{n_1! n_2!}p_1^{n_1} p_2^{n_2},\qquad \frac{n!}{n_1!n_2!}={n\choose n_1,n_2}= {n \choose n_1}={n\choose n_2}, </tex>
| |
| - |
| |
| - | ::<tex>2\le k \le n <\infty, \qquad n_1+n _2=n, \qquad p_1+p_2=1,</tex>
| |
| - |
| |
| - | определённых на точечных пространствах элементарных событий
| |
| - |
| |
| - | ::<tex>\Omega_1, \Omega _2</tex>
| |
| - |
| |
| - | и принимающих в дискретные последовательные моменты времени
| |
| - |
| |
| - | ::<tex>t_1, t_2, \quad t_i<t_{i+1}</tex>
| |
| - |
| |
| - | целые неотрицательные значения
| |
| - |
| |
| - | ::<tex>n_1, n_2,</tex>
| |
| - |
| |
| - | взаимосвязанные условием
| |
| - |
| |
| - | ::<tex>n_1 +n_2=n,</tex>
| |
| - |
| |
| - | согласно которому
| |
| - |
| |
| - | ::<tex>X_2=n_2 \mid X_1=n_1</tex>
| |
| - |
| |
| - | если в первый момент времени <tex>t_1</tex> первая случайная величина <tex>X_1</tex> приняла значение
| |
| - |
| |
| - | ::<tex>n_1, \quad 0\le n_1\le n,</tex>
| |
| - |
| |
| - | то во второй момент времени <tex>t_2</tex>вторая случайная величина
| |
| - | <tex>X _2</tex> принимает значение
| |
| - |
| |
| - | ::<tex> n _2, \quad 0\le n_2\le n- n_1.</tex>
| |
| - |
| |
| - | ==Характер зависимости случайных величин в каждом цикле экспериментов:==
| |
| - |
| |
| - | *только первая случайная величина является независимой, а вторая случайная величина зависима от первой;
| |
| - |
| |
| - | * если первая случайная величина в первый момент времени приняла своё максимально возможное значение, равное <tex>X_1=n</tex>, то вторая случайная величина во второй момент времени обязана принять своё минимальное (нулевое) значение <tex>X_2=n_2=0</tex> в противном случае не будет выполнено условие суммирования числовых значений случайных величин распределения, согласно которому <tex>n_1+n _2=n</tex>;
| |
| - |
| |
| - | * если первая случайная величина в первый момент времени приняла своё минимальное (нулевое) значение <tex>X_1=n_1=0</tex>, то вторая случайная величина во второй момент времени обязана принять своё максимальное значение <tex>X_2=n_2=n</tex> в противном случае не будет выполнено условие <tex>n_1+n _2=n</tex>.
| |
| - |
| |
| - |
| |
| - | ==Характеристики случайных величин биномиального распределения:==
| |
| - |
| |
| - | пространство элементарных событий
| |
| - |
| |
| - | ::<tex>\Omega_i(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=[0 \le n_i \le n-n_{i-1}],</tex>
| |
| - |
| |
| - | вероятность
| |
| - |
| |
| - | ::<tex>P(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})={n-n_{i-1}\choose n_i}p_i^{n_i},</tex>
| |
| - |
| |
| - | математическое ожидание
| |
| - |
| |
| - | ::<tex>E(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=(n-n_{i-1})p_i,</tex>
| |
| - |
| |
| - | Дисперсия
| |
| - |
| |
| - | ::<tex>D(t_i,X_i \mid t_{i-1},X_{i-1})=(n -n_{i-1})p_iq_i, \quad q_i=1-p_i,</tex>
| |
| - |
| |
| - | производящая
| |
| - |
| |
| - | ::<tex>A(s_i)=(1+p_is_i)^{n-n_{i-1}}</tex>
| |
| - |
| |
| - | и характеристическая
| |
| - |
| |
| - | ::<tex>f(t_i)=(1+p_ie^{jt_i})^{n-n_{i-1}}</tex>
| |
| - |
| |
| - | функции.
| |
| - |
| |
| - | ==Характеристики биномиального распределения:==
| |
| - |
| |
| - | пространство элементарных событий
| |
| - |
| |
| - | ::<tex>\sum_{i=1}^2\Omega_i(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1}), </tex>
| |
| - |
| |
| - | расположенное в точках <tex>t_1, t_2</tex> временной последовательности,
| |
| - |
| |
| - | вероятность
| |
| - |
| |
| - | ::<tex>\prod_{i=1}^2P(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=\frac{n!}{n_1!n_2!}p_1^{n_1}p_2^{n_2},</tex>
| |
| - | дисперсия
| |
| - |
| |
| - | ::<tex>\sum_{i=1}^2D(t_i,X_i \mid t_{i-1},X_{i-1})=\sum_{i=1}^2(n-n_{i-1})p_iq_i,</tex>
| |
| - |
| |
| - | ковариационная матрица <tex>B=\| b_{ij} \|</tex>, где
| |
| - |
| |
| - | ::<tex>b_{ij} = \begin{cases} (n-n_{i-1})p_iq_i, & i=j,\\0, & i \not= j,\end{cases}</tex>
| |
| - |
| |
| - | корреляционная матрица <tex>P=\| \rho_{ij} \|</tex>, где
| |
| - |
| |
| - | ::<tex>\rho _{ij} = \begin{cases} 1, & i=j,\\0, & i \not= j,\end{cases}</tex>
| |
| - |
| |
| - | ::<tex>\chi^2</tex> - квадрат критерий для полиномиально распределенных случайных величин
| |
| - |
| |
| - | ::<tex>\chi^2=\sum_{i=1}^2 [X_i-(n -n_{i-1})p_i^{(0)}]^2/(n -n_{i-1})p_i^{(0)}= </tex>
| |
| - |
| |
| - | ::<tex>=-n+\sum_{i=1}^2X_i^2 /(n-n_{i-1})p_i^{(0)}.</tex>
| |
| - |
| |
| - | '''Урновая модель биномиального распределения''' содержит одну исходную урну и две приёмные урны. В начальный момент времени исходная урна содержит <tex>n</tex>- множество различимых неупорядоченных элементов, а приёмные урны пусты.
| |
| - | Объем каждой из них не менее объёма исходной урны. Нумерация приёмных урн соответствует нумерации случайных величин биномиального распределения.
| |
| - |
| |
| - | Первая [[выборка]]
| |
| - |
| |
| - | ::<tex>n_1,\quad 0\le n_1\le n</tex>
| |
| - |
| |
| - | в первый момент времени направляется в первую приёмную урну с вероятностью <tex>p_1</tex> каждого элемента.
| |
| - |
| |
| - | Во второй момент времени все оставшиеся <tex>n-n_1</tex> элементы исходной урны, образующие вторую выборку
| |
| - |
| |
| - | ::<tex>n_2,\quad 0\le n-n_1\le n,</tex>
| |
| - |
| |
| - | направляются во вторую приёмную урну с вероятностью <tex>p_2</tex> каждого элемента.
| |
| - |
| |
| - | В результате исходная урна пуста, а все её элементы размещены в приёмных урнах.
| |
| - |
| |
| - | После обработки результатов разбиения множества на подмножества элементы возвращают на прежнее место, и урновая модель готова к проведению очередного цикла зависимых экспериментов.
| |
| - |
| |
| - | Произведение вероятностей попадания <tex>n_1, n_2</tex> элементов в две приёмные урны есть '''биномиальное распределение. '''
| |
| - |
| |
| - | ==Математическое ожидание биномиального распределения==
| |
| - |
| |
| - | получают одним из двух способов: как максимум произведения математических ожиданий его случайных величин, или как максимум вероятности распределения.
| |
| - |
| |
| - | '''Необходимые'''
| |
| - |
| |
| - | ::<tex>k=n, \qquad n_i=1, \qquad 0<p_i<1,</tex>
| |
| - |
| |
| - | '''и достаточные'''
| |
| - |
| |
| - | ::<tex>p_1=p_2=2^{-1}</tex>
| |
| - |
| |
| - | '''условия''' получения математического ожидания биномиального распределения.
| |
| - |
| |
| - | Математическое ожидание
| |
| - |
| |
| - | ::<tex>\left(\prod_{i=1}^2E(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})\right)_{max}=\left(\prod_{i=1}^2(n-n_{i-1})p_i\right)_{max}=\frac{n!}{n^n}=\frac{1}{2},</tex>
| |
| - |
| |
| - | максимальная вероятность
| |
| - |
| |
| - | ::<tex>\left(\prod_{i=1}^2P(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})\right)_{max}=\left(\frac{n!}{n_i!n_2!}p_1^{n_1}p_2^{n_2}\right)_{max}=\frac{n!}{n^n}= \frac{1}{2}</tex>
| |
| - |
| |
| - | равна математическому ожиданию,
| |
| - |
| |
| - | максимальная дисперсия
| |
| - |
| |
| - | ::<tex>D(X_1,X_2|X_1)_{max}=\left(\sum_{i-1}^2(n-n_{i-1})p_iq_i \right)_{max}=\frac{n^2-1}{2n}=\frac{3}{4}.</tex>
| |
| - |
| |
| - | Пространство элементарных событий биномиального распределения при получении его математического ожидания
| |
| - |
| |
| - | ::<tex>\Omega(t_1, X_1=n_1=1 \mid t_2,X_2=n_2=1)</tex>
| |
| - |
| |
| - | расположено в точках <tex>t_1, t_2</tex> временной последовательности.
| |
| - |
| |
| - | '''Урновая модель получения математического ожидания биномиального распределения''' содержит одну исходную урну и две приёмные урны единичных объемов. Нумерация приёмных урн соответствует нумерации случайных величин биномиального распределения.
| |
| - |
| |
| - | В начальный момент времени исходная урна содержит два различимых элемента, а приёмные урны пусты.
| |
| - |
| |
| - | В первый момент времени из исходной урны выбирают один элемент <tex>n_1=1</tex> и направляют его в первую приёмную урну с вероятностью <tex>p_1=0,5</tex> .
| |
| - |
| |
| - | Во второй момент времени оставшийся элемент <tex>n_2=1</tex> исходной урны отправляют во вторую приёмную урну с вероятностью <tex>p_2=0,5</tex>.
| |
| - |
| |
| - | В результате исходная урна пуста, а её два элемента по одному размещены в приёмных урнах. После обработки результатов разбиения исходного множества на два подмножества все элементы из приёмных урн возвращают в исходную урну. На этом один цикл повторных зависимых экспериментов закончен, и урновая модель готова к проведению следующего цикла экспериментов.
| |
| - |
| |
| - | Произведение вероятностей попадания по одному произвольному элементу в каждую приёмную урну есть '''математическое ожидание биномиального распределения. '''
| |
| - |
| |
| - | '''Изменение характеристик биномиального распределения в окрестности его математического ожидания''' приведено в таблице 2.
| |
| - |
| |
| - | {|border=1 align="center"
| |
| - | |+Таблица 2 – Окрестности математического ожидания биномиального распределения настоящей интерпретации 21-го века
| |
| - | | Числовые значения первой случайной величины <tex>X_1=n_1</tex>
| |
| - | | Числовые значения второй случайной величины <tex>X_2=n_2| X_1=n_1</tex>
| |
| - | |Вероятность распределения
| |
| - | |Дисперсия распределения
| |
| - | |Математическое ожидание распределения
| |
| - | |-
| |
| - | |1
| |
| - | |1
| |
| - | |0,50
| |
| - | |0,75
| |
| - | |0,50
| |
| - | |-
| |
| - | |2
| |
| - | |0
| |
| - | |0,25
| |
| - | |0,50
| |
| - | |rowspan=2 |
| |
| - | |-
| |
| - | |0
| |
| - | |2
| |
| - | |0,25
| |
| - | |0,50
| |
| - | |}
| |
| - |
| |
| - | Вероятность биномиального распределения как функция двух переменных является симметричной функцией относительно своего математического ожидания.
| |
| - |
| |
| - | ==Биномиальное распределение как процесс выполнения взаимосвязанных действий над объектами==
| |
| - |
| |
| - | [[Объект | Объекты]]: [[множество | множество]], его [[подмножества | подмножества]] и их [[элемент | элементы]] как объективная [[реальность | реальность]], существующая вне нас и независимо от нас.
| |
| - | Биномиальное распределение это:
| |
| - |
| |
| - | * [[случайный процесс | случайный процесс ]] безвозвратного разделения последовательно во времени <tex> t_1, t_2 </tex> и в пространстве конечного <tex> n</tex>- множества различимых неупорядоченных элементов на две части <tex> n_1, n_2 </tex> случайных объёмов, сумма которых равна объёму исходного множества: <tex> n_1+ n_2=n, \quad 2\le n<\infty </tex>,
| |
| - |
| |
| - | * разделение множества осуществляют [[выборка | выборками]] без возвращения (изъятые из множества элементы не возвращают обратно во множество до полного окончания экспериментов),
| |
| - |
| |
| - | * вероятность попадания одного произвольного элемента множества в каждое из подмножеств принимают за вероятность случайной величины [[ распределение Бернулли |распределения Бернулли]] с положительным исходом <tex> 0\le p_i<1, \quad i=1,2</tex>,
| |
| - |
| |
| - | * результаты испытаний Бернулли неизменны во время проведения разбиения множества и пронормированы <tex> \sum _{i=1}^2 p_i =1</tex> согласно [[аксиоматика Колмогорова | аксиоматике Колмогорова]],
| |
| - | * очерёдность следования выборок принимают за очередность следования во времени и нумерацию случайных величин <tex> X_1, X_2 </tex> биномиального распределения,
| |
| - |
| |
| - | *случайный объём каждой выборки <tex> n_i, \quad i=1,2</tex> в момент времени <tex> t_i, \quad i=1,2</tex> принимают за числовое значение соответствующей случайной величины <tex> X_i=n_i, \quad i=1,2</tex> биномиального распределения,
| |
| - |
| |
| - | * первая случайная величина биномиального распределения является независимой и может принимать любое случайное значение в пределах от нуля до числового значения исходного множества <tex> X_1=n_1, \quad 0\le n_1\le n<\infty </tex>,
| |
| - |
| |
| - | * вторая случайная величина биномиального распределения принимает числовое значение <tex> n_2 </tex>, равное числу элементов множества оставшееся после изъятия из него первой выборкой случайного числа элементов <tex> n_1: \quad n_2=n-n_1 </tex>,
| |
| - |
| |
| - | * результаты каждого разбиения обрабатывают вероятностными методами, определяют технические характеристике всех выборок и принимают их за технические характеристики случайных величин биномиального распределения,
| |
| - |
| |
| - | * минимально необходимый набор технических характеристик случайных величин и биномиального распределения в целом это: [[пространство элементарных событий | пространство элементарных событий]], [[ вероятность ]], [[математическое ожидание |математическое ожидание]] и [[дисперсия |дисперсия]],
| |
| - |
| |
| - | * математическое ожидание биномиального распределения имеет место, когда число выборок <tex>k</tex> равно числу элементов <tex> n</tex>-множества <tex> k=n</tex> и численно равно <tex> \frac{n!}{n^n}=\frac{2!}{2^2}=\frac{1}{2} </tex>.
| |
| - |
| |
| - | ==Сравнительная оценка характеристик биномиальных распределений настоящей и традиционной интерпретаций==
| |
| - |
| |
| - | Цель сравнительной оценки показать, что биномиальное распределение настоящей интерпретации соответствует, а биномиальное распределение традиционной интерпретации не соответствует современным требованиям аксиоматики Колмогорова.
| |
| - |
| |
| - | Несоответствие состоит в том, что, во-первых, биномиальное распределение традиционной интерпретации представлено распределением одной случайной величины, а по своей сути и определению оно должно быть распределением двух случайных величин.
| |
| - |
| |
| - | Во-вторых, при неограниченном увеличении числа независимых испытаний ( <tex>n </tex>) математическое ожидание (<tex>np </tex>) биномиального распределения традиционной интерпретации устремляется к бесконечности, что недопустимо, поскольку сумма всех вероятностей распределения, включая и его математическое ожидание, в любом распределении обязана быть равной единице (см., например, таблицу 1). Кроме того, математическое ожидание (<tex>np_1 </tex>) и дисперсия (<tex>np_1q_1 </tex>) первой случайной величины биномиального распределения настоящей интерпретации приняты за математическое ожидание (<tex>np </tex>) и дисперсию (<tex>npq</tex>) биномиального распределения традиционной интерпретации.
| |
| - |
| |
| - | Историческая справка <ref> http://ru.wikiznanie.org/wiki/ Биномиальное распределение, Настоящая интерпретация 21-го века, раздел Историческая справка</ref>
| |
| - |
| |
| - | ==Связь с другими распределениями==
| |
| - |
| |
| - | Если <tex>k>2</tex>,то получаем [[мультиномиальное распределение]] распределение настоящей интерпретации 21-го века.
| |
| | | | |
| | | | |
| | | | |
| | [[Категория:Вероятностные распределения]] | | [[Категория:Вероятностные распределения]] |
Более того, справедлива следующая оценка. Пусть 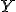 — случайная величина, имеющая распределение Пуассона с параметром
— случайная величина, имеющая распределение Пуассона с параметром 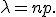 Тогда для произвольного множества
Тогда для произвольного множества 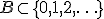 справедливо неравенство:
справедливо неравенство:
Доказательство и обзор более точных результатов, касающихся точности данного приближения, можно найти в [1, гл. III, §12].
близко к стандартному нормальному.
Данная теорема используется для приближенного вычисления вероятностей отдельных значений биномиального распределения. Она утверждает [1, гл. I, §6], что равномерно по всем значениям 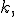 таким что
таким что ^{2/3},) имеет место
имеет место
На практике необходимость оценки вероятностей отдельных значений, которую дает локальная теорема Муавра-Лапласа, возникает нечасто. Гораздо более важно оценивать вероятности событий, включающих в себя множество значений. Для этого используется интегральная теорема, которую можно сформулировать в следующем виде [1, гл. I, §6]:
Есть ряд результатов, позволяющих оценить скорость сходимости. В [1, гл. I, §6] приводится следующий результат, являющийся частным случаем теоремы Берри-Эссеена:
Заметим, что асимптотический результат не изменится, если заменить строгие неравенства на нестрогие и наоборот. Предельная вероятность от такой замены также не поменяется, так как нормальное распределение абсолютно непрерывно и вероятность принять любое конкретное значение для него равна нулю. Однако исходная вероятность от такой замены может измениться, что вносит в формулу некоторую неоднозначность. Для больших значений 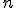 изменение будет невелико, однако для небольших
изменение будет невелико, однако для небольших 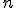 это может внести дополнительную погрешность.
это может внести дополнительную погрешность.
Для устранения этой неоднозначности, а также повышения точности приближения рекомендуется задавать интересующие события в виде интервалов с полуцелыми границами. При этом приближение получается точнее. Это связано с тем интуитивно понятным соображением, что аппроксимация кусочно-постоянной функции (функции распределения биномиального закона) с помощью непрерывной функции дает более точные приближения между точками разрыва, чем в этих точках.
Применим нормальное приближение с той расстановкой неравенств, которая дана выше (снизу строгое, сверху нестрогое):
1. Ширяев А.Н. Вероятность. — М.: МЦНМО, 2004.
принимающей целочисленные значения
с вероятностями:
называемым числом испытаний, и вещественным числом
называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из
независимых испытаний, в каждом из которых может произойти "успех" с вероятностью
то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы
независимых слагаемых, имеющих распределение Бернулли.
при
распределение симметрично относительно центра
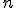
велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно.
В этих случаях можно использовать приближения биномиального распределения распределением Пуассона и нормальным (приближение Муавра-Лапласа).
большие, а значения
близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром
и
таким образом, что
то
— случайная величина, имеющая распределение Пуассона с параметром
Тогда для произвольного множества
справедливо неравенство:
а
фиксировано. Это приближение можно рассматривать как частный случай центральной предельной теоремы, применение которой основано на представлении
в виде суммы
слагаемых. Приближение основано на том, что при указанных условиях распределение нормированной величины
где
таким что
имеет место
— плотность стандартного нормального распределения.
при
имеет стандартное нормальное распределение
и аппроксимирующая вероятность определяется по формуле
— функция распределения стандартного нормального закона:
— функция распределения случайной величины
На практике решение о том, насколько следует доверять нормальному приближению, принимают исходя из величины
Чем она больше, тем меньше будет погрешность приближения.
изменение будет невелико, однако для небольших
это может внести дополнительную погрешность.
Оценим вероятность того, что число успехов будет отличаться от наиболее вероятного значения
не более чем на
. Заметим, что значение
очень мало, поэтому применение нормального приближения здесь довольно ненадежно.
.
— примерно в 5 раз меньше, чем в предыдущем подходе.

