Графические модели (курс лекций)/2014/Задание 1

Материал из MachineLearning.

(Различия между версиями)

Перейти к: навигация, поиск

Версия 19:30, 11 февраля 2014

Основная статья: Графические модели (курс лекций)

Содержание

1 Вероятностные модели посещаемости курса
2 Вариант 1
3 Вариант 2
4 Вариант 3
5 Оформление задания
6 Распределение студентов по вариантам

Начало выполнения задания: 12 февраля 2014 г.
Срок сдачи: 26 февраля 2014 г., 23:59.

Среда для выполнения задания — MATLAB.

Вероятностные модели посещаемости курса

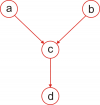
Рассмотрим модель посещаемости студентами одного курса лекции. Пусть аудитория данного курса состоит из студентов профильной кафедры, а также студентов других кафедр. Обозначим через $a$ количество студентов, распределившихся на профильную кафедру, а через $b$ — количество студентов других кафедр на курсе. Пусть студенты профильной кафедры посещают курс с некоторой вероятностью $p_1$ , а студенты остальных кафедр — с вероятностью $p_2$ . Обозначим через $c$ количество студентов на данной лекции. Тогда случайная величина $c|a,b$ есть сумма двух случайных величин, распределенных по биномиальному закону $B(a,p_1)$ и $B(b,p_2)$ соответственно. Пусть далее на лекции по курсу ведется запись студентов. При этом каждый студент записывается сам, а также, быть может, записывает своего товарища, которого на лекции на самом деле нет. Пусть студент записывает своего товарища с некоторой вероятностью $p_3$ . Обозначим через $d$ общее количество записавшихся на данной лекции. Тогда случайная величина $d|c$ представляет собой сумму $c$ и случайной величины, распределенной по биномиальному закону $B(c,p_3)$ . Для завершения задания вероятностной модели осталось определить априорные вероятности для $a$ и для $b$ . Пусть обе эти величины распределены равномерно в своих интервалах $[a_{min},a_{max}]$ и $[b_{min},b_{max}]$ . Таким образом, мы определили следующую вероятностную модель:
Модель 1

$p(a,b,c,d)=p(d|c)p(c|a,b)p(a)p(b)$ ,

$d|c \sim c + B(c,p_3)$ ,
$c|a,b \sim B(a,p_1) + B(b,p_2)$ ,
$a \sim R[a_{min},a_{max}]$ ,
$b \sim R[b_{min},b_{max}]$ .

Графическая модель для вероятностной модели 1

Рассмотрим несколько упрощенную версию модели 1. Известно, что биномиальное распределение $B(n,p)$ при большом количестве испытаний и маленькой вероятности успеха может быть с высокой точностью приближено пуассоновским распределением $Poiss(\lambda)$ с $\lambda = np$ . Известно также, что сумма двух пуассоновских распределений с параметрами $\lambda_1$ и $\lambda_2$ есть пуассоновское распределение с параметром $\lambda_1+\lambda_2$ . Таким образом, мы можем сформулировать вероятностную модель, которая является приближенной версией модели 1:
Модель 2
$p(a,b,c,d)=p(d|c)p(c|a,b)p(a)p(b)$ ,
$d|c \sim c + B(c,p_3)$ ,
$c|a,b \sim Poiss(ap_1+bp_2)$ ,
$a \sim R[a_{min},a_{max}]$ ,
$b \sim R[b_{min},b_{max}]$ .

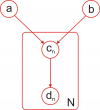
Рассмотрим теперь модель посещаемости нескольких лекций курса. Будем считать, что посещаемости отдельных лекций являются независимыми. Тогда:
Модель 3

$p(a,b,c_1,\dots,c_N,d_1,\dots,d_N)=\prod_{n=1}^Np(d_n|c_n)p(c_n|a,b)p(a)p(b)$ ,

$d_n|c_n \sim c_n + B(c_n,p_3)$ ,
$c_n|a,b \sim B(a,p_1) + B(b,p_2)$ ,
$a \sim R[a_{min},a_{max}]$ ,
$b \sim R[b_{min},b_{max}]$ .

Графическая модель для вероятностной модели 3

По аналогии с моделью 2 можно сформулировать упрощенную модель для модели 3:
Модель 4
$p(a,b,c_1,\dots,c_N,d_1,\dots,d_N)=\prod_{n=1}^Np(d_n|c_n)p(c_n|a,b)p(a)p(b)$ ,
$d_n|c_n \sim c_n + B(c_n,p_3)$ ,
$c_n|a,b \sim Poiss(ap_1+bp_2)$ ,
$a \sim R[a_{min},a_{max}]$ ,
$b \sim R[b_{min},b_{max}]$ .

Задание состоит из трех вариантов. Распределение студентов по вариантам см. ниже.

Вариант 1

Рассматривается модель 2 с параметрами $a_{min}=15, a_{max}=30, b_{min}=250, b_{max}=350, p_1 = 0.5, p_2 = 0.05, p_3 = 0.5$ . Провести на компьютере следующие исследования:

Найти математические ожидания и дисперсии априорных распределений для всех параметров $a, b, c, d$ .
Пронаблюдать, как происходит уточнение прогноза для величины $c$ по мере прихода новой косвенной информации. Для этого построить графики и найти мат.ожидание и дисперсию для распределений $p(c), p(c|b), p(c|a,b), p(c|a,b,d)$ при параметрах $a,b,d$ , равных мат.ожиданиям своих априорных распределений, округленных до ближайшего целого.
Определить, какая из величин $a,b,d$ вносит больший вклад в уточнение прогноза для величины $c$ (в смысле дисперсии распределения). Для этого убедиться в том, что $\mathbb{D}[c|d]<\mathbb{D}[c|b]$ и $\mathbb{D}[c|d]<\mathbb{D}[c|a]$ для любых допустимых значений $a,b,d$ . Найти множество точек $(a,b)$ таких, что $\mathbb{D}[c|b]<\mathbb{D}[c|a]$ . Являются ли множества $\{(a,b)|\mathbb{D}[c|b]<\mathbb{D}[c|a]\}$ и $\{(a,b)|\mathbb{D}[c|b]\ge\mathbb{D}[c|a]\}$ линейно разделимыми?
Провести временные замеры по оценке всех необходимых распределений $p(c),p(c|a),p(c|b),p(c|d),p(c|a,b),p(c|a,b,d),p(d)$ .
Провести исследования из пп. 1-4 для точной модели 1 и сравнить результаты с аналогичными для модели 2. Привести пример оценки параметра, в котором разница между моделью 1 и 2 проявляется в большой степени.

Взять в качестве диапазона допустимых значений для величины $c$ интервал $[0,a_{max}+b_{max}]$ , а для величины $d$ — интервал $[0,2*(a_{max}+b_{max})]$ .

При оценке выполнения задания будет учитываться эффективность программного кода. В частности, временные затраты на расчет отдельного распределения не должны превышать одной секунды.

Вариант 2

Найти математические ожидания и дисперсии априорных распределений для всех параметров $a, b, c, d$ .
Пронаблюдать, как происходит уточнение прогноза для величины $b$ по мере прихода новой косвенной информации. Для этого построить графики и найти мат.ожидание и дисперсию для распределений $p(b), p(b|a), p(b|a,d)$ при параметрах $a,d$ , равных мат.ожиданиям своих априорных распределений, округленных до ближайшего целого.
Определить, при каких соотношениях параметров $p_1,p_2$ изменяется относительная важность параметров $a,b$ для оценки величины $c$ . Для этого найти множество точек $\{(p_1,p_2)|\mathbb{D}[c|b]<\mathbb{D}[c|a]\}$ при $a,b$ , равных мат.ожиданиям своих априорных распределений, округленных до ближайшего целого. Являются ли множества $\{(p_1,p_2)|\mathbb{D}[c|b]<\mathbb{D}[c|a]\}$ и $\{(p_1,p_2)|\mathbb{D}[c|b]\ge\mathbb{D}[c|a]\}$ линейно разделимыми?
Провести временные замеры по оценке всех необходимых распределений $p(c),p(c|a),p(c|b),p(b|a),p(b|a,d),p(d)$ .
Провести исследования из пп. 1-4 для точной модели 1 и сравнить результаты с аналогичными для модели 2. Привести пример оценки параметра, в котором разница между моделью 1 и 2 проявляется в большой степени.

Вариант 3

Рассматривается модель 4 с параметрами $a_{min}=15, a_{max}=30, b_{min}=250, b_{max}=350, p_1 = 0.5, p_2 = 0.05, p_3 = 0.5, N = 50$ . Провести на компьютере следующие исследования:

Найти математические ожидания и дисперсии априорных распределений для всех параметров $a, b, c_n, d_n$ .
Реализовать генератор выборки $d_1,\dots,d_N$ из модели при заданных значениях параметров $a,b$ .
Пронаблюдать, как происходит уточнение прогноза для величины $b$ по мере прихода новой косвенной информации. Для этого построить графики и найти мат.ожидание и дисперсию для распределений $p(b), p(b|d_1), \dots, p(b|d_1,\dots,d_N)$ , где выборка $d_1,\dots,d_N$ 1) сгенерирована из модели при параметрах $a,b$ , равных мат.ожиданиям своих априорных распределений, округленных до ближайшего целого и 2) $d_1=\dots=d_N$ , где $d_n$ равно мат.ожиданию своего априорного распределения, округленного до ближайшего целого. Провести аналогичный эксперимент, если дополнительно известно значение $a$ . Сравнить результаты двух экспериментов.
Провести временные замеры по оценке всех необходимых распределений $p(c_n),p(d_n),p(b|d_1,\dots,d_n),p(b|a,d_1,\dots,d_n)$ .
Провести исследования из пп. 1-4 для точной модели 3 и сравнить результаты с аналогичными для модели 4.

Оформление задания

Выполненное задание следует отправить письмом по адресу bayesml@gmail.com с заголовком письма «[ГМ14] Задание 1 <ФИО>». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Также убедительная просьба строго придерживаться заданных ниже прототипов реализуемых функций.

Присланный вариант задания должен содержать в себе:

Текстовый файл в формате PDF с указанием ФИО и номера варианта, содержащий описание всех проведенных исследований.
Все исходные коды с необходимыми комментариями.

Исходные коды должны включать в себя реализацию оценки распределений в виде отдельных функций. Прототип для функции оценки распределения $p(c|a,d)$ для модели 2 имеет следующий вид:

Оценка распределения $p(c|a,d)$ для модели 2

[p, c, m, v] = p2c_ad(a, d, params)

ВХОД

a — значение параметра a;

d — значение параметра d;

params — набор параметров вероятностной модели, структура с полями 'amin', 'amax', 'bmin', 'bmax', 'p1', 'p2', 'p3';

ВЫХОД

p — распределение вероятности, вектор-столбец длины length(c);

c — носитель распределения, вектор-столбец;

m — математическое ожидание распределения;

v — дисперсия распределения.

Прототипы функций для других распределений выглядят аналогично. Если в распределении переменных до или после | несколько, то в названии функции они идут в алфавитном порядке. Функция для оценки распределения $p(b|a,d_1,\dots,d_N)$ для модели 3 имеет название p3b_ad, а входной параметр $d$ является одномерным массивом длины $N$ .

Генерация из распределения $p(d_1,\dots,d_N|a,b)$ для модели 3

d = m3_generate(N, a, b, params)

ВХОД

N — количество лекций;

a — значение параметра a;

b — значение параметра b;

params — набор параметров вероятностной модели, структура с полями 'amin', 'amax', 'bmin', 'bmax', 'p1', 'p2', 'p3';

ВЫХОД

d — значения $d_1,\dots,d_N$ , вектор-столбец длины N.

Распределение студентов по вариантам

№ п/п	Студент	Вариант
1	Алешин Илья	1
2	Антипов Алексей	1
3	Арбузова Дарья	2
4	Горелов Алексей	2
5	Зиннурова Эльвира	1
6	Ломов Никита	1
7	Львов Сергей	2
8	Найдин Олег	2
9	Никифоров Андрей	1
10	Новиков Александр	3
11	Петров Григорий	2
12	Подоприхин Дмитрий	3
13	Рыжков Александр	3
14	Сокурский Юрий	2
15	Ульянов Дмитрий	3
16	Харациди Олег	1
17	Шабашев Федор	3
18	Шадриков Андрей	3

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%93%D1%80%D0%B0%D1%84%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B8_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%29/2014/%D0%97%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5_1»

@@ Строка 166: / Строка 166: @@
  | align="center"|1 || Алешин Илья || 1
  |-
- | align="center"|2 || Антипов Алексей || 3
+ | align="center"|2 || Антипов Алексей || 1
  |-
- | align="center"|3 || Арбузова Дарья || 3
+ | align="center"|3 || Арбузова Дарья || 2
  |-
- | align="center"|4 || [[Участник:Algor|Горелов Алексей]] || 3
+ | align="center"|4 || [[Участник:Algor|Горелов Алексей]] || 2
  |-
- | align="center"|5 || Зиннурова Эльвира || 2
+ | align="center"|5 || Зиннурова Эльвира || 1
  |-
  | align="center"|6 || Ломов Никита || 1
  |-
- | align="center"|7 || Львов Сергей || 1
+ | align="center"|7 || Львов Сергей || 2
  |-
  | align="center"|8 || Найдин Олег  || 2
  |-
- | align="center"|9 || Никифоров Андрей || 2
+ | align="center"|9 || Никифоров Андрей || 1
  |-
- | align="center"|10 || Новиков Александр || 1
+ | align="center"|10 || Новиков Александр || 3
  |-
  | align="center"|11 || Петров Григорий || 2
  |-
- | align="center"|12 || Подоприхин Дмитрий || 2
+ | align="center"|12 || Подоприхин Дмитрий || 3
  |-
  | align="center"|13 || [[Участник:Alex.Ryzhkov|Рыжков Александр]] || 3
@@ Строка 196: / Строка 196: @@
  | align="center"|16 || Харациди Олег || 1
  |-
- | align="center"|17 || Шабашев Федор || 1
+ | align="center"|17 || Шабашев Федор || 3
  |-
- | align="center"|18 || [[Участник:SdvAnd|Шадриков Андрей]] || 1
+ | align="center"|18 || [[Участник:SdvAnd|Шадриков Андрей]] || 3
  |-
  |}

Графические модели (курс лекций)/2014/Задание 1

Материал из MachineLearning.

Версия 19:30, 11 февраля 2014

Содержание

Вероятностные модели посещаемости курса

Вариант 1

Вариант 2

Вариант 3

Оформление задания

Распределение студентов по вариантам

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты