Участник:Lr2k/Песочница

Материал из MachineLearning.

(Различия между версиями)

Версия 10:27, 13 октября 2008

Содержание

1 Введение
- 1.1 Постановка математической задачи
2 Изложение метода
- 2.1 Формула прямоугольников
- 2.2 Формула трапеций
3 Числовой пример
4 Рекомендации программисту
- 4.1 Автоматический выбор шага интегрирования
5 Заключение
6 Список литературы

Введение

Постановка математической задачи

Одной из основных задач численного анализа является задача об интерполяции функций. Пусть на отрезке $a\le \x\le \b$ задана сетка $\omega=\{x_i:x_0=a<x_1<\cdots<x_i<\cdots<x_n=b\}$ и в её узлах заданы значения функции $y(x)$ , равные $y(x_0)=y_0,\cdots,y(x_i)=y_i,\cdots,y(x_n)=y_n$ . Требуется построить интерполянту — функцию $f(x)$ , совпадающую с функцией $y(x)$ в узлах сетки:

( 1 )

$f(x_i)=y_i, i=0,1,\cdots,n.$

Основная цель интерполяции — получить быстрый (экономичный) алгоритм вычисления значений $f(x)$ для значений $x$ , не содержащихся в таблице данных.

Интерполируюшие функции $f(x)$ , как правило строятся в виде линейных комбинаций некоторых элементарных функций:

$f(x)=\sum_{k=0}^N {c_k\Phi_k(x)},$

где $\{\Phi_k(x)\}$ — фиксированный линейно независимые функции, $c_0, c_1, \cdots, c_n$ — не определенные пока коэффициенты.

Из условия (1) получаем систему из $n+1$ уравнений относительно коэффициентов $\{c_k\}$ :

$\sum_{k=0}^N {c_k\Phi_k(x_i)}=y_i, i=0,1,\cdots,n.$

Предположим, что система функций $\Phi_k(x)$ такова, что при любом выборе узлов $a<x_1<\cdots<x_i<\cdots<x_n=b$ отличен от нуля определитель системы:

$\Delta(\Phi) = \begin{vmatrix} \Phi_0(x_0) & \Phi_1(x_0) & \cdots & \Phi_n(x_0) \\\Phi_0(x_1) & \Phi_1(x_1) & \cdots & \Phi_n(x_1)\\ \hdotsfor{4} \\\Phi_0(x_n) & \Phi_1(x_n) & \cdots & \Phi_n(x_n)\end{vmatrix}$ .

Тогда по заданным $y_i (i=1,\cdots, n)$ однозначно определяются коэффициенты $c_k (k=1,\cdots, n)$ .

Изложение метода

Интерполяция кубическими сплайнами является частным случаем кусочно-полиномиальной интерполцией. В этом специальном случае между любыми двумя соседними узлами функция интерполируется кубическим полиномом. его коэффициенты на каждом интервале определяются из условий сопряжения в узлах:

$\begin{multline}f_i=y_i, f'(x_i-0)=f'(x_i+0), f''(x_i-0)=f''(x_i+0), i=1, 2, \cdots, n-1.\end{multiline}$

Кроме того, на границе при $x=x_0$ и $x=x_n$ ставятся условия

( 2 )

$f''(x_0)=0, f''(x_n)=0.$

Будем искать кубический полином в виде

( 2 )

$f''(x_0)=0, f''(x_n)=0.$

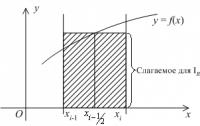
Формула прямоугольников

Рис.2

Заменим интеграл (3) выражением $f(x_{i-1/2})h$ , где $x_{i-1/2}=x_{i}-0.5h.$

Тогда получим формулу

( 5 )

$\int_{x_{i-1}}^{x_i}{f(x)dx}\approx f(x_{i-1/2})h,$

которая называется формулой прямоугольников на частичном отрезке $[x_{i-1},x_i].$

Погрешность метода (5) определяется величиной

$\psi_{i}=\int_{x_{i-1}}^{x_i}{f(x)dx}-f(x_{i-1/2})h$

которую легко оценить с помощью формулы Тейлора. Действительно, запишем $\psi_{i}$ в виде

( 6 )

$\psi_{i}=\int_{x_{i-1}}^{x_i}{(f(x)-f(x_{i-1/2}))dx}$

и воспользуемся разложением

$f(x)=f(x_{i-1/2})+(x-x_{i-1/2})f'(x_{i-1/2})+\frac{(x-x_{i-1/2})^2}{2}f''(\xi),$

где $\xi_i=\xi_i(x)\in [x_{i-1},x_i]$ . Тогда из (6) получим

$\psi_{i}=\int_{x_{i-1}}^{x_i}{\frac{(x-x_{i-1/2})^2}{2}f''(\xi_i)dx}$

Обозначая $M_{2,i}=\underset{x\in [x_{i-1},x_i]}{max}|f''(x)|$ , оценим $\psi_i$ следующим образом:

$|\psi_i|\le M_{2,i} \int_{x_{i-1}}^{x_i}{\frac{(x-x_{i-1/2})^2}{2}dx}=\frac{h^3}{24}M_{2,i}$

Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка

( 7 )

$|\psi_i|\le \frac{h^3}{24}M_{2,i}$

т.е. формула имеет погрешность $O(h^3)$ при $h\rightarrow0$ .

Заметим,что оценка (7) является неулучшаемой, т.е. существует функция $f(x)$ , для которой (7) выполняется со знаком равенства. Действительно, для $f(x)=(x-x_{i-1/2})^2$ имеем $M_{2,i}=2, f(x_{i-1/2})=0$ и

$\int_{x_{i-1}}^{x_i}{f(x)dx}-f(x_{i-1/2})h=\frac{h^3}{24}M_{2,i}$

Суммируя равенства (5) по $i$ от $1$ до $N$ , получим составную формулу прямоугольников

( 8 )

$\int_{a}^{b}{f(x)dx}\approx \sum_{i=1}^N{f(x_{i-1/2})h}$

Погрешность этой формулы

$\Psi=\int_{a}^{b}{f(x)dx}-\sum_{i=1}^N{f(x_{i-1/2})h}$

равна сумме погрешностей по всем частичным отрезкам,

$\Psi=\sum_{i=1}^N{\psi_i}=\sum_{i=1}^N{\int_{x_{i-1}}^{x_i}{\frac{(x-x_{i-1/2})^2}{2}f''(\xi_i)dx}}$

Отсюда, обозначая $M_2=\underset{x\in [a,b]}{max}|f''(x)|$ , получим

( 9 )

$|\Psi|\le\frac{M_2Nh^3}{24}=\frac{h^2(b-a)}{24}M_2$

т.е. погрешность формулы прямоугольников на всем отрезке есть велицина $O(h^2)$ .

В этом случае говорят, что квадратурная формула имеет второй порядок точнотси.

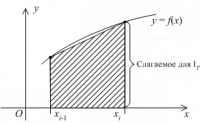
Формула трапеций

Рис.3

На частичном отрезке эта формула имеет вид

( 10 )

$\int_{x_{i-1}}^{x_i}{f(x)dx}\approx \frac{f(x_{i-1})+f(x_i)}{2}h$

и получается путем замены подынтегральной функции $f(x)$ интерполяционным многочленом первой степени,постоенным по узлам $x_{i-1},x_i$ , т.е. функцией

$L_{1,i}(x)=\frac{1}{h}((x-x_{i-1})f(x_i)-(x-x_i)f(x_{i-1})).$

Для оценки погрешности достаточно вспомнить,что

$f(x)-L_{1,i}(x)=\frac{(x-x_{i-1})(x-x_i)}{2}f''(\xi_i(x)).$

Отсюда получим

$\psi_i=\int_{x_{i-1}}^{x_i}{f(x)dx}-\frac{f(x_{i-1})+f(x_i)}{2}h=\int_{x_{i-1}}^{x_i}{(f(x)-L_{1,i}(x))dx}=\int_{x_{i-1}}^{x_i}{\frac{(x-x_{i-1})(x-x_i)}{2}f''(\xi_i(x))dx}$

и,следовательно,

( 11 )

$|\psi_i|\le \frac{M_{2,i}h^3}{12}$

Оценка (11) неулучшаема, так как в ней достигается равенство, например, для $f(x)=(x-x_i)^2$ .

Составная формула трапеций имеет вид

( 12 )

$\int_{a}^{b}{f(x)dx}\approx \sum_{i=1}^N{\frac{f(x_{i-1})+f(x_i)}{2}h}=h(0.5f_0+f_1+...+f_{N-1}+0.5f_N),$

где $f_i=f(x_i),i=0,1,...,N,hN=b-a$ .

Погрешность этой формулы оценивается следующим образом:

( 13 )

$|\Psi|\le \frac{h^2(b-a)}{12}M_2,M_2=\underset{x\in [a,b]}{max}|f''(x)|$

Таким образом, формула трапеций имеет, так же как и формула прямоугольников, второй порядок точности, $\Psi=O(h^2)$ , но ее погрешность оценивается величиной в два раза большей.

Числовой пример

Вычислим по формулам прямоугольников и трапеций при $n=2$ интеграл

( 14 )

$I=\int_{0}^{\pi/2}{\sin(x)dx} = 1$

В данном случае

$P_2=\frac{\pi}{4}(\sin(\frac{\pi}{8})+\sin(\frac{3\pi}{8}))=1.026172$

$T_2=\frac{\pi}{4}(\frac{1}{2}\sin(0)+\sin(\frac{\pi}{4})+\frac{1}{2}\sin(\frac{\pi}{2}))=0.948059$

Зная точный ответ (14), найдем погрешности

( 15 )

$\alpha_2=-0.026172,\beta_2=0.051941$

Вторая производная функции $\sin(x)$ на отрезке $[0,\pi/2]$ отрицательна, ее модуль не превышает единицы: $M_2=1$ . Величина погрешностей (15) удовлетворяет неравенствам (9) и (13):

$|\alpha_2|\le \frac{1}{96}(\frac{\pi}{2})^3<0.041,|\beta_2|\le \frac{1}{48}(\frac{\pi}{2})^3<0.081$

Рекомендации программисту

Автоматический выбор шага интегрирования

Величина погрешности численного интегрирования зависит как от шага сетки $h$ , так и от гладкости подынтегральной функции $f(x)$ . Например, в оценку (11), наряду с $h$ , входит величина

$M_{2,i}=\underset{x\in [x_{i-1},x_i]}{max}|f''(x)|,$

которая может сильно меняться от точки к точке и, вообще говоря, заранее неизвестна. Если величина погрешности велика, то ее можно уменьшить путем измельчения сетки на данном отрезке $[x_{i-1},x_i]$ . Для этого прежде всего надо уметь апостериорно, т.е. после проведения расчета, оценивать погрешность.

Апостериорную оценку погрешности можно осуществить методом Рунге. Пусть какая-то квадратурная формула имеет на частичном отрезке порядок точности $m$ , т.е. $I_i-I_{h,i}\approx c_i h_i^m$ . Тогда

$I_i-I_{h/2,i}\approx c_i (\frac{h_i}{2})^m,$

откуда получим

( 16 )

$I_i-I_{h,i}\approx 2^m (I_i-I_{h/2,i}),$

( 17 )

$I_i-I_{h/2,i}\approx \frac{I_{h/2,i}-I_{h,i}}{2^m-1}$

Возможность апостериорно оценивать погрешность позволяет вычислять интеграл (1) с заданной точностью $\epsilon >0$ путем автоматического выбора шага интегрирования $h_i$ . Пусть используется составная квадратурная формула

$I\approx I_h=\sum_{i=1}^N{I_{h,i}}$

где $I_{h,i}$ - квадратурная сумма на частичном отрезке, причем на каждом частичном отрезке используется одна и та же квадратурная формула (например, формула трапеций). Проведем на каждом частичном отрезке $[x_{i-1},x_i]$ все вычисления дважды, один раз - с шагом $h_i$ и второй раз - с шагом $0.5h_i$ и оценим погрешность по правилу Рунге (17).

Если для заданного $\epsilon >0$ будут выполняться неравенства

( 18 )

$|I_i-I_{h/2,i}|\approx \frac{|I_{h/2,i}-I_{h,i}|}{2^m-1} \le \frac{\epsilon h_i}{b-a},i=1,2,...,N,$

то получим

$|I-I_h/2|\le \frac{\epsilon}{b-a}\sum_{i=1}^N{h,i}=\epsilon,$

т.е. будет достигнута заданная точность $\epsilon$ .

Если же на каком-то из частичных отрезков оценка (18) не будет выполняться, то шаг на этом отрезке надо измельчить еще в два раза и снова оценить погрешность. Измельчение сетки на данном отрезке следует проводить до тех пор, пока не будет достигнута оценка вида (18). Заметим, что для некоторой функции $f(x)$ такое измельчение может продолжаться слишком долго. Поэтому в соответствующей программе следует предусмотреть ограничение сверху на число измельчений,а также вожможность увеличения $\epsilon$ .

Таким образом, автоматический выбор шага интегрирования приводит к тому, что интегрирование ведется с крупным шагом на участках плавного изменения функции $f(x)$ и с мелким шагом - на участках быстрого изменения $f(x)$ . Это позволяет при заданной точности $\epsilon$ уменьшить количество вычислений значений $f(x)$ по сравнению с расчетом на сетке с постоянным шагом. Подчеркнем, что для нахождения сумм $I_{h/2,i}$ не надо пересчитывать значения $f(x)$ во всех узлах, достаточно вычислять $f(x)$ только в новых узлах.

Заключение

Список литературы

А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
А.А.Самарский. Введение в численные методы М.: Наука, 1982.

Это незавершённая статья. Вы поможете проекту, исправив и дополнив её.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:Lr2k/%D0%9F%D0%B5%D1%81%D0%BE%D1%87%D0%BD%D0%B8%D1%86%D0%B0»

Категории: Незавершённые статьи | Численное интегрирование

@@ Строка 19: / Строка 19: @@
 Предположим, что система функций <tex>\Phi_k(x)</tex> такова, что при любом выборе узлов <tex>a<x_1<\cdots<x_i<\cdots<x_n=b</tex> отличен от нуля определитель системы:
-<p align="center"><tex>\Delta(\Phi) = \begin{vmatrix} \Phi_0(x_0) & \Phi_1(x_0) & \cdots & \Phi_n(x_0) \\\Phi_0(x_1) & \Phi_1(x_1) & \cdots & \Phi_n(x_1)\\ \cdots & \cdots & \cdots & \cdots  \\\Phi_0(x_n) & \Phi_1(x_n) & \cdots & \Phi_n(x_n)\end{vmatrix}</tex>.</p>
+<p align="center"><tex>\Delta(\Phi) = \begin{vmatrix} \Phi_0(x_0) & \Phi_1(x_0) & \cdots & \Phi_n(x_0) \\\Phi_0(x_1) & \Phi_1(x_1) & \cdots & \Phi_n(x_1)\\ \hdotsfor{4}  \\\Phi_0(x_n) & \Phi_1(x_n) & \cdots & \Phi_n(x_n)\end{vmatrix}</tex>.</p>
 Тогда по заданным <tex>y_i (i=1,\cdots, n)</tex> однозначно определяются коэффициенты <tex>c_k (k=1,\cdots, n)</tex>.
@@ Строка 25: / Строка 25: @@
 == Изложение метода ==
 Интерполяция кубическими сплайнами является частным случаем кусочно-полиномиальной интерполцией. В этом специальном случае между любыми двумя соседними узлами функция интерполируется кубическим полиномом. его коэффициенты на каждом интервале определяются из условий сопряжения в узлах:
-<math>f_i=y_i,
+<p align="center"><tex>\begin{multline}f_i=y_i,
 f'(x_i-0)=f'(x_i+0),
-f''(x_i-0)=f''(x_i+0), i=1, 2, \cdots, n-1.</math>
+f''(x_i-0)=f''(x_i+0), i=1, 2, \cdots, n-1.\end{multiline}</tex></p>
 Кроме того, на границе при <tex>x=x_0</tex> и <tex>x=x_n</tex> ставятся условия
-<math>f''(x_0)=0, f''(x_n)=0</math>
+{{ eqno | 2 }}
+<p align="center"><tex>f''(x_0)=0, f''(x_n)=0.</tex></p>
+Будем искать кубический полином в виде
+{{ eqno | 2 }}
+<p align="center"><tex>f''(x_0)=0, f''(x_n)=0.</tex></p>
 === Формула прямоугольников ===