Интерполяция каноническим полиномом
Материал из MachineLearning.
| Строка 3: | Строка 3: | ||
Пусть задана функция ''f(x)'' на отрезке [''a,b'']. Задача интерполяции состоит в построении функции ''g(x)'', совпадающей с ''f(x)'' в некотором наборе точек ''x<sub>0</sub>, x<sub>1</sub>,...,x<sub>n</sub>'' из отрезка [''a,b'']. Эти точки называются узлами интерполяции. Также должно выполняться условие: ''g(x<sub>k</sub>) = y<sub>k</sub>, k=0,...,n,'' где ''y<sub>k</sub> = f(x<sub>k</sub>).'' | Пусть задана функция ''f(x)'' на отрезке [''a,b'']. Задача интерполяции состоит в построении функции ''g(x)'', совпадающей с ''f(x)'' в некотором наборе точек ''x<sub>0</sub>, x<sub>1</sub>,...,x<sub>n</sub>'' из отрезка [''a,b'']. Эти точки называются узлами интерполяции. Также должно выполняться условие: ''g(x<sub>k</sub>) = y<sub>k</sub>, k=0,...,n,'' где ''y<sub>k</sub> = f(x<sub>k</sub>).'' | ||
| - | === | + | === Полином в каноническом виде === |
Известно, что любая непрерывная на отрезке [a,b] функция f(x) может быть хорошо приближена некоторым полиномом P<sub>n</sub>(x). | Известно, что любая непрерывная на отрезке [a,b] функция f(x) может быть хорошо приближена некоторым полиномом P<sub>n</sub>(x). | ||
| Строка 12: | Строка 12: | ||
<tex>f(x)=P_n(x)=c_0+c_1x+c_2x^2+ \ldots + c_nx^n </tex> | <tex>f(x)=P_n(x)=c_0+c_1x+c_2x^2+ \ldots + c_nx^n </tex> | ||
| - | Коэффициенты полинома <tex>c_i</tex> определим из условий Лагранжа <tex>P_n(x_i)=y_i</tex>, <tex>i=1, \ldots, n</tex>, что с учётом предыдущего выражения даёт систему уравнений с ''n''+1 неизвестными: | + | Коэффициенты полинома <tex>c_i</tex> определим из условий Лагранжа <tex>P_n(x_i)=y_i</tex>, <tex>i=1, \ldots, n</tex>, что с учётом предыдущего выражения даёт систему линейных алгебраических уравнений с ''n''+1 неизвестными: |
<tex> | <tex> | ||
| Строка 48: | Строка 48: | ||
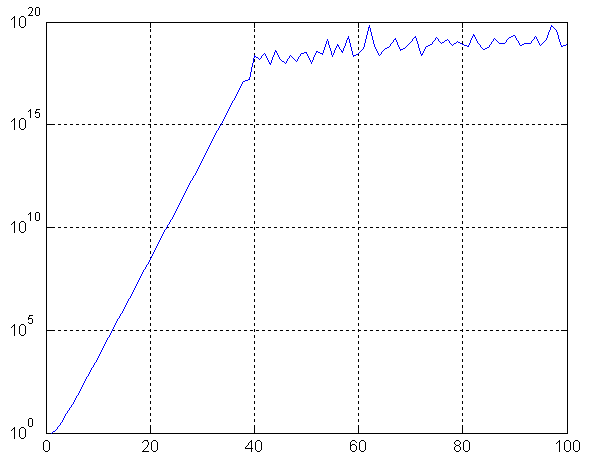
При достаточной простоте реализации метода он имеет существенный недостаток: число обусловленности матрицы быстро растёт с увеличением числа узлов интерполяции, что можно показать на следующем графике | При достаточной простоте реализации метода он имеет существенный недостаток: число обусловленности матрицы быстро растёт с увеличением числа узлов интерполяции, что можно показать на следующем графике | ||
| - | + | [[Изображение:Report1-fig1.gif|Зависимость числа обусловленности матрицы от количества узлов интерполяции]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
Из-за плохой обусловленности матрицы рекомендуется применять другие методы интерполяции (например, метод Лагранжа). При этом важно понимать, что при теоретическом принемении различных методов они приводят к одинаковому результату, т.е. мы получим один и тот же полином. | Из-за плохой обусловленности матрицы рекомендуется применять другие методы интерполяции (например, метод Лагранжа). При этом важно понимать, что при теоретическом принемении различных методов они приводят к одинаковому результату, т.е. мы получим один и тот же полином. | ||
| Строка 58: | Строка 54: | ||
Однако при практической реализации мы получим полиномы различной точности аппроксимации из-за погрешности вычислений аппаратуры. | Однако при практической реализации мы получим полиномы различной точности аппроксимации из-за погрешности вычислений аппаратуры. | ||
| - | === | + | === Способ вычисления полинома в точке === |
Чтобы изобразить графически аппроксимирующий полином, необходимо вычислить его значение в ряде точек. Это можно сделать следующими способами. | Чтобы изобразить графически аппроксимирующий полином, необходимо вычислить его значение в ряде точек. Это можно сделать следующими способами. | ||
| Строка 75: | Строка 71: | ||
== Анализ метода == | == Анализ метода == | ||
| - | === | + | === Сложность вычислений === |
| + | Оценка сложности интерполирования функции складывается из количества операций для решения СЛАУ и нахождения значения полинома в точке. | ||
| + | Сложность решения СЛАУ (системы линейных алгебраических уравнений), например, методом Гаусса для матрицы размера ''n''x''n'': 2''n''<sup>3</sup>/3, т.е. O(''n''<sup>3</sup>). | ||
| - | === | + | Для нахождения полинома в заданной точке требуется ''n'' умножений и ''n'' сложений. В результате сложность метода: O(''n''<sup>3</sup>). |
| + | |||
| + | === Погрешность интерполяции === | ||
Предположим, что на отрезке интерполирования [''a,b''] функция ''f(x)'' ''n'' раз непрерывно-дифференцируема. Погрешность интерполяции складывается из погрешности самого метода и ошибок округления. | Предположим, что на отрезке интерполирования [''a,b''] функция ''f(x)'' ''n'' раз непрерывно-дифференцируема. Погрешность интерполяции складывается из погрешности самого метода и ошибок округления. | ||
| Строка 93: | Строка 93: | ||
Если максимальное значение производной ''f<sup>n+1</sup>(x)'' равно <tex>M_{n+1} = \sup_{x \in [x_0, x_n]} \left| f^{n+1}(x) \right| ,</tex> то для погрешности интерполяции следует оценка: <tex>\left| R_n(x) \right| = \frac{M_{n+1}}{(n+1)!}\omega_n(x).</tex> | Если максимальное значение производной ''f<sup>n+1</sup>(x)'' равно <tex>M_{n+1} = \sup_{x \in [x_0, x_n]} \left| f^{n+1}(x) \right| ,</tex> то для погрешности интерполяции следует оценка: <tex>\left| R_n(x) \right| = \frac{M_{n+1}}{(n+1)!}\omega_n(x).</tex> | ||
| - | === | + | При реализации данного метода на ЭВМ ошибкой интерполяции ''E<sub>n</sub>(x)'' будем считать максимальное уклонение полинома от исходной функции на выбранном промежутке: <tex>E_n(x) = \max_{x \in [a, b]} \left| f(x) - P_n(x) \right| .</tex> |
| + | |||
| + | === Выбор узлов интерполяции === | ||
Ясно, что от выбора узлов интерполируемой функции напрямую зависит, насколько точно многочлен будет являться её приближением. | Ясно, что от выбора узлов интерполируемой функции напрямую зависит, насколько точно многочлен будет являться её приближением. | ||
| Строка 130: | Строка 132: | ||
Известно, что для любого полинома ''p<sub>k</sub>(x)'' степени ''k'' с коэффициентом, равным единице при старшей производной верно неравенство <tex>\max_{x \in [-1,1]}p_k(x) \geq \frac1{2^{k-1}},</tex> т.е. полиномы Чебышева являются полиномами, наименее уклоняющимися от нуля. | Известно, что для любого полинома ''p<sub>k</sub>(x)'' степени ''k'' с коэффициентом, равным единице при старшей производной верно неравенство <tex>\max_{x \in [-1,1]}p_k(x) \geq \frac1{2^{k-1}},</tex> т.е. полиномы Чебышева являются полиномами, наименее уклоняющимися от нуля. | ||
| + | |||
| + | == Вычислительный эксперимент == | ||
| + | |||
| + | Для реализации поставленной задачи была написана программа на языке С++, которая по заданной функции приближает её каноническим полиномом. Разумеется, необходимо указать узлы, через которые полином пройдёт, и значения функции в этих узлах. | ||
| + | |||
| + | Далее строится СЛАУ, которая решается методом Гаусса. На выходе получаем коэффициенты для полинома и ошибку аппроксимации. | ||
| + | |||
| + | Как было показано выше, и в чём мы убедимся в дальнейшем, от выбора узлов зависит точность, с которой полином будет приближать функцию. | ||
| + | |||
| + | === Пример 1: Интерполяция синуса === | ||
| + | |||
| + | Попробуем интерполировать функцию y = sin(x) на отрезке [1, 8.5]. Выберем узлы интерполяции: {1.1, 2, 4.7, 7.5, 8.5} | ||
| + | |||
| + | Полученный в результате интерполяции полином отображён на рисунке (синим цветом показан график y = sin(x), красным – интерполяционного полинома) | ||
| + | |||
| + | [[Изображение:Report1-fig2.gif]] | ||
| + | |||
| + | Ошибка интерполяции в этом случае: 0.1534 | ||
| + | |||
| + | Давайте посмотрим, что произойдёт, если выбрать равномерно стоящие узлы {2, 3.5 5, 6.5, 8} для той же функции на том же отрезке. | ||
| + | |||
| + | На отрезке [3, 6] приближение, бесспорно, стало лучше. Однако разброс на краях очень большой. Ошибка интерполяции: 2.3466 | ||
| + | |||
| + | [[Изображение:Report1-fig3.gif]] | ||
| + | |||
== Смотри также == | == Смотри также == | ||
Версия 12:31, 18 октября 2008
Содержание |
Постановка задачи
Пусть задана функция f(x) на отрезке [a,b]. Задача интерполяции состоит в построении функции g(x), совпадающей с f(x) в некотором наборе точек x0, x1,...,xn из отрезка [a,b]. Эти точки называются узлами интерполяции. Также должно выполняться условие: g(xk) = yk, k=0,...,n, где yk = f(xk).
Полином в каноническом виде
Известно, что любая непрерывная на отрезке [a,b] функция f(x) может быть хорошо приближена некоторым полиномом Pn(x).
Справедлива следующая Теорема (Вейерштрасса): Для любого >0 существует полином Pn(x) степени
, такой, что
В качестве аппроксимирующей функции выберем полином степени n в каноническом виде:
Коэффициенты полинома определим из условий Лагранжа
,
, что с учётом предыдущего выражения даёт систему линейных алгебраических уравнений с n+1 неизвестными:
Обозначим систему таких уравнений символом (*) и перепишем её следующим образом:
или в матричной форме: где
- вектор-столбец, содержащий неизвестные коэффициенты
,
- вектор-столбец, составленный из табличных значений функции
, а матрица
имеет вид:
Система линейных алгебраических уравнений (*) относительно неизвестных иметь единственное решение, если определитель матрицы
отличен от нуля.
Определитель матрицы называют определителем Вандермонда, его можно вычислить по следующей формуле:
Число узлов интерполяционного полинома должно быть на единицу больше его степени. Это понятно из интуитивных соображений: через 2 точки можно провести единственную прямую, через 3 - единственную параболу и т.д. Но полином может получиться и меньшей степени. Т.е. если 3 точки лежат на одной прямой, то через них пройдёт единственный полином первой степени (но это ничему не противоречит: просто коэффициент при старшей степени равен нулю).
При достаточной простоте реализации метода он имеет существенный недостаток: число обусловленности матрицы быстро растёт с увеличением числа узлов интерполяции, что можно показать на следующем графике
Из-за плохой обусловленности матрицы рекомендуется применять другие методы интерполяции (например, метод Лагранжа). При этом важно понимать, что при теоретическом принемении различных методов они приводят к одинаковому результату, т.е. мы получим один и тот же полином.
Однако при практической реализации мы получим полиномы различной точности аппроксимации из-за погрешности вычислений аппаратуры.
Способ вычисления полинома в точке
Чтобы изобразить графически аппроксимирующий полином, необходимо вычислить его значение в ряде точек. Это можно сделать следующими способами.
Первый способ. Можно посчитать значение a1x и сложить с a0. Далее найти a2x2, сложить с полученным результатом, и так далее. Таким образом, на j-ом шаге вычисляется значение ajxj и складывается с уже вычисленной суммой .
Вычисление значения ajxj требует j операций умножения. Т.е. для подсчёта многочлена в заданной точке требуется (1 + 2 + ... + n) = n(n+1)/2 операций умножения и n операций сложения. Всего операций в данном случае: Op1 = n(n+1)/2 + n.
Второй способ. Полином можно также легко вычислить с помощью так называемой схемы Горнера:
Для вычисления значения во внутренних скобках anx + an-1 требуется одна операция умножения и одна операция сложения. Для вычисления значения в следующих скобках (anx + an-1)x + an-2 требуется опять одна операция умножения и одна операция сложения, т.к. anx + an-1 уже вычислено, и т.д.
Тогда в этом способе вычисление Pn(x) потребует n операций умножения и n операций сложения, т.е. сложность вычислений Op2 = n+n = 2n. Ясно, что Op2 << Op1.
Анализ метода
Сложность вычислений
Оценка сложности интерполирования функции складывается из количества операций для решения СЛАУ и нахождения значения полинома в точке.
Сложность решения СЛАУ (системы линейных алгебраических уравнений), например, методом Гаусса для матрицы размера nxn: 2n3/3, т.е. O(n3).
Для нахождения полинома в заданной точке требуется n умножений и n сложений. В результате сложность метода: O(n3).
Погрешность интерполяции
Предположим, что на отрезке интерполирования [a,b] функция f(x) n раз непрерывно-дифференцируема. Погрешность интерполяции складывается из погрешности самого метода и ошибок округления.
Ошибка приближения функции f(x) интерполяционным полиномом n-ой степени Pn(x) в точке x определяется разностью: Rn(x) = f(x) - Pn(x).
Погрешность Rn(x) определяется следующим соотношением:
Здесь - производная (n+1)-го порядка функции f(x) в некоторой точке
а функция
определяется как
Если максимальное значение производной fn+1(x) равно то для погрешности интерполяции следует оценка:
При реализации данного метода на ЭВМ ошибкой интерполяции En(x) будем считать максимальное уклонение полинома от исходной функции на выбранном промежутке:
Выбор узлов интерполяции
Ясно, что от выбора узлов интерполируемой функции напрямую зависит, насколько точно многочлен будет являться её приближением.
Введём следующее определение: полиномом Чебышева называется многочлен вида
Известно (см. ссылки литературы), что если узлы интерполяции x0, x1,...,xn являются корнями полинома Чебышева степени n+1, то величина принимает наименьшее возможное значение по сравнению с любым другим выбором набора узлов интерполяции.
Очевидно, что в случае k = 1 функция T1(x), действительно, является полиномом первой степени, поскольку T1(x) = cos(arccos x) = x.
В случае k = 2 T2(x) тоже полином второй степени. Это нетрудно проверить. Воспользуемся известным тригонометрическим тождеством: cos2θ = 2cos²θ - 1, положив θ = arccos x.
Тогда получим следующее соотношение: T2(x) = 2x² - 1.
С помощью тригонометрического тождества cos(k + 1)θ = 2cosθcoskθ - cos(k - 1) легко показать, что для полиномов Чебышева справедливо реккурентное соотношение:
Tk+1(x) = 2xTk(x) - Tk-1(x)
При помощи данного соотношения можно получить формулы для полиномов Чебышева любой степени.
Корни полинома Чебышева легко находятя из уравнения: Tk(x) = cos(k arccos x) = 0. Получаем, что уравнение имеет k различных корней, расположенных на отрезке [-1,1]: которые и следует выбирать в качестве узлов интерполирования.
Нетрудно видеть, что корни на [-1,1] расположены симметрично и неравномерно - чем ближе к краям отрезка, тем корни расположены плотнее. Максимальное значение модуля полинома Чебышева равно 1 и достигается в точках
Если положить то для того, чтобы коэффициент при старшей степени полинома ωk(x) был равен 1,
Известно, что для любого полинома pk(x) степени k с коэффициентом, равным единице при старшей производной верно неравенство т.е. полиномы Чебышева являются полиномами, наименее уклоняющимися от нуля.
Вычислительный эксперимент
Для реализации поставленной задачи была написана программа на языке С++, которая по заданной функции приближает её каноническим полиномом. Разумеется, необходимо указать узлы, через которые полином пройдёт, и значения функции в этих узлах.
Далее строится СЛАУ, которая решается методом Гаусса. На выходе получаем коэффициенты для полинома и ошибку аппроксимации.
Как было показано выше, и в чём мы убедимся в дальнейшем, от выбора узлов зависит точность, с которой полином будет приближать функцию.
Пример 1: Интерполяция синуса
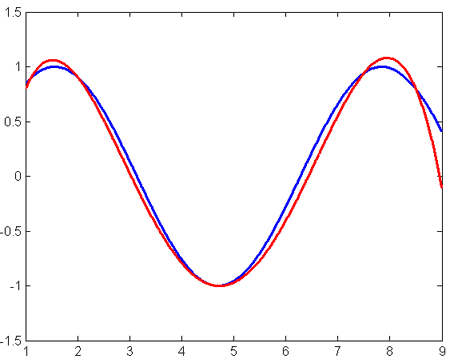
Попробуем интерполировать функцию y = sin(x) на отрезке [1, 8.5]. Выберем узлы интерполяции: {1.1, 2, 4.7, 7.5, 8.5}
Полученный в результате интерполяции полином отображён на рисунке (синим цветом показан график y = sin(x), красным – интерполяционного полинома)
Ошибка интерполяции в этом случае: 0.1534
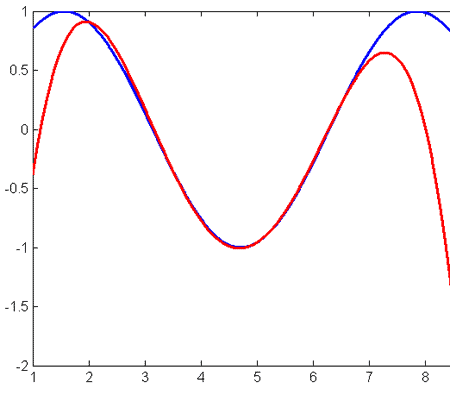
Давайте посмотрим, что произойдёт, если выбрать равномерно стоящие узлы {2, 3.5 5, 6.5, 8} для той же функции на том же отрезке.
На отрезке [3, 6] приближение, бесспорно, стало лучше. Однако разброс на краях очень большой. Ошибка интерполяции: 2.3466