Интерполяция полиномами Лагранжа и Ньютона

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Содержание

1 Постановка задачи
2 Метод решения задачи
- 2.1 Полином Лагранжа
- 2.2 Полином Ньютона
3 Погрешность интерполирования
4 Выбор узлов интерполяции
5 Пример
6 Рекомендации программисту
7 Выводы
8 Литература
9 Смотри также

Постановка задачи

Пусть задана функция $y = f(x)$ .
Пусть заданы точки $\bf{X} = \{ x_i | i = 1..n \}$ из некоторой области $\bf D$ .
Пусть значения функции $f$ известны только в этих точках.
Точки $\bf{X}$ называют узлами интерполяции.
$\delta x_i = x_i - x_{i-1}$ - шаг интерполяционной сетки.
Задача интерполяции состоит в поиске такой функции $F$ из заданного класса функций, что $F(x_i) = y_i$

Метод решения задачи

Полином Лагранжа

Представим интерполяционную функцию в виде полинома
$P_n(x) = \sum_{i=0}^n y_i Q_{n,i}(x)$
где $Q_{n,i}(x)$ - полиномы степели n вида:
$Q_{n,i}(x) = \prod_{j=0, j\neq i}^{n} \frac{(x-x_j)}{(x_i-x_j)}$
Очевидно, что $Q_{n,i}(x)$ принимает значение 1 в точке $x_i$ и 0 в остальных узлах интерполяции. Следовательно в точке $x_i$ исходный полином принимает значение $y_i$
Таким образом, построенный полином $P_n(x)$ является интерполяционным полиномом для функции $y = f(x)$ на сетке $\bf{X}$ .

Полином Ньютона

Интерполяционный полином в форме Лагранжа не удобен для вычислений тем, что при увеличении числа узлов интерполяции приходится перестраивать весь полином заново.
Перепишем полином Лагранжа в другом виде:
$P_n(x) = P_0(x) + \sum_{i=1}^n{(P_i(x) - P_{i-1}(x))}$
где $P_i(x)$ - полиномы Лагранжа степени i ≤ n.
Пусть $Q_i(x) = P_i(x) - P_{i-1}(x) \qquad(*)$
. Этот полином имеет степень i и обращается в нуль при $x = x_0, x = x_1, ..., x = x_{i-1}{$ .
Поэтому он представим в виде:
$Q_i(x) = A_i(x - x_0)...(x - x_{i-1})$ , где $A_i$ - коэффициент при $x^i$ . Так как $x^i$ не входит в $P_{i-1}(x)$ , то $A_i$ совпадает с коэффициентом при $x^i$ в полиноме $P_i(x)$ . Таким образом из определения $P_i(x)$ получаем:
$A_i = \sum_{k=0}^i\frac{f(x_k)}{w_{k,i}}$
где
$w_{k,i} = (x_k - x_0)...(x_k - x_{k-1})(x_k - x_{k+1})...(x_k - x_i)$
Препишем формулу $\qquad(*)$ в виде
$P_n(x) = P_{n-1} + A_n(x - x_0)...(x - x_{n-1})$
Рекуррентно выражая $P_i(x)$ пролучам окончательную формулу для полинома:
$P_n(x) = A_0 + A_1(x-x_0) + ...+ A_n(x - x_0)...(x - x_{n-1})$
Такое представление полинома удобно для вычисления, потому что увеличение числа узлов на единицу требует добавления только одного слагаемого.

Погрешность интерполирования

Поставим вопрос о том, насколько хорошо интерполяционный полином $P_n(x)$ приближает функцию $f(x)$ на отрезке [a,b].
Рассмотри м остаточный член:
$R_n(x) = f(x) - P_n(x)$ , x ∈ [a, b].
По определению интерполяционного полинома $<br>R_n(x_i) = 0, x_i \in \bf X$
поэтому речь идет об оценке $R_n(x)$ при значениях $x \not= x_i$ .
Пусть $f(x)$ имеет непрерывную (n+1) производную на отрезке [a, b].
Тогда погрешность определяется формулой:
$|R_n(x)| = \frac{f^{n+1}(\varepsilon)}{(n+1)!}w_{n+1}(x)$ ,
где $w_{n+1} = (x - x_0)...(x - x_n)$ ,
$\varepsilon$ - точка из [a, b].
Так как точка $\varepsilon$ наизвестна, то эта формула позволяет только оценить погрешность:
$|R_n(x)| \le \frac{M_{n+1}}{(n+1)!}|w_{n+1}(x)|$
где $M_{n+1} = \max_{x\in[\alpha, \beta]}|f^{n+1}(x)|$
Из вида множетеля $w_{n+1}$ следует, что оценка имеет смысл только при $x \in [x_0, x_n]$ . Если это не так, то при интерполяции используются полиномы низких степеней (n = 1,2).

Выбор узлов интерполяции

Так как от выбора узлов завист точность интерполяции, то возникает вопрос о том, как их выбирать. С помощью выбора узлов можно минимизировать значение $w_{n+1}$ в оценке погрешности. Эта задача решается с помощью многочлена Чебышева [1]:
$T_{n+1}(x) = \frac{(b - a)}{(2^{2n+1})}cos ((n + 1)arccos \frac{2x - (b + a)}{(b - a)})$
В качестве узлов следут взять корни этого многочлена, то есть точки:
$x_k = \frac{a + b}{2} + \frac{b - a}{2} \cos\frac{(2k + 1)\pi}{2(n + 1)}$

Пример

В качастве примера рассмотрим интерполяцию синуса. Возьмем равномерную решетку x = [-3,-1.5,0,1.5,3];
Интерполяция полиномом Лагранжа:

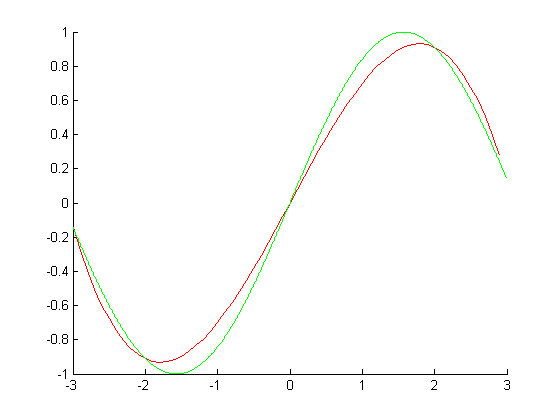
Ошибка(максимальное отклонение от sin(x) на отрезке):0.1423
Интерполяция полиномом Ньютона:
Ошибка:
Возьмем решетку x с узлами в корнях полинома Чебышева= [-2.8531,-1.7632,0,1.7634,2.8532];
Интерполяция полиномом Лагранжа:

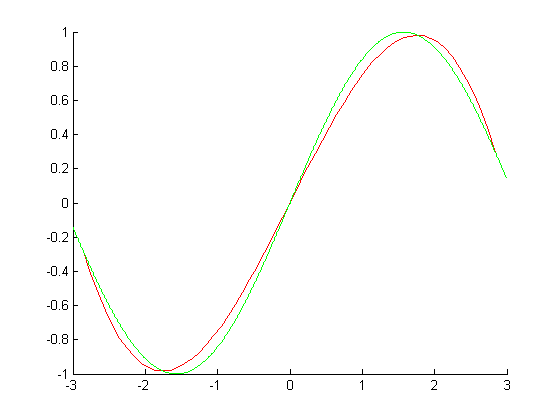
Ошибка: 0.0944
Интерполяция полиномом Ньютона:
Ошибка:

Выводы

Литература

Самарский А.А. Гулин А.В. Численные методы 1989г.
Костомаров Д.П., Фаворский А.П. Вводные лекции по численным методам

Смотри также

Практикум ММП ВМК, 4й курс, осень 2008

Это незавершённая статья. Вы поможете проекту, исправив и дополнив её.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%98%D0%BD%D1%82%D0%B5%D1%80%D0%BF%D0%BE%D0%BB%D1%8F%D1%86%D0%B8%D1%8F_%D0%BF%D0%BE%D0%BB%D0%B8%D0%BD%D0%BE%D0%BC%D0%B0%D0%BC%D0%B8_%D0%9B%D0%B0%D0%B3%D1%80%D0%B0%D0%BD%D0%B6%D0%B0_%D0%B8_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0»

Категории: Незавершённые статьи | Учебные задачи

@@ Строка 22: / Строка 22: @@
 <tex> y = f(x) </tex> на сетке <tex> \bf{X} </tex>. <br>
 ===Полином Ньютона===
-Интерполяционный полином в форме Лагранжа не удобен для вычислений тем, что при увеличении числа узло интерполции приходится перестраивать весь полином заного.<br>
+Интерполяционный полином в форме Лагранжа не удобен для вычислений тем, что при увеличении числа узлов интерполяции приходится перестраивать весь полином заново.<br>
 Перепишем полином Лагранжа в другом виде:<br>
 <tex>P_n(x) = P_0(x) + \sum_{i=1}^n{(P_i(x) - P_{i-1}(x))} </tex><br>
 где <tex>P_i(x)</tex> - полиномы Лагранжа степени i ≤ n.<br>
-Пусть <tex>Q_i(x) = P_i(x) - P_{i-1}(x) \qquad(*)</tex> <br>. Этот полином инеет степень i и обращается в нуль при
+Пусть <tex>Q_i(x) = P_i(x) - P_{i-1}(x) \qquad(*)</tex> <br>. Этот полином имеет степень i и обращается в нуль при
 <tex>x = x_0, x = x_1, ..., x = x_{i-1}{</tex>. <br>
 Поэтому он представим в виде:<br>
 <tex>Q_i(x) = A_i(x - x_0)...(x - x_{i-1})</tex>,
-где <tex>A_i</tex> - коэффициент при <tex>x^i</tex>. Так как <tex>x^i</tex> не входити в <tex>P_{i-1}(x)</tex>, то <tex>A_i</tex> совпадает с коэффициентом при <tex>x^i</tex> в полиноме <tex>P_i(x)</tex>. Таким образом из определения <tex>P_i(x)</tex> получаем:<br>
+где <tex>A_i</tex> - коэффициент при <tex>x^i</tex>. Так как <tex>x^i</tex> не входит в <tex>P_{i-1}(x)</tex>, то <tex>A_i</tex> совпадает с коэффициентом при <tex>x^i</tex> в полиноме <tex>P_i(x)</tex>. Таким образом из определения <tex>P_i(x)</tex> получаем:<br>
 <tex> A_i = \sum_{k=0}^i\frac{f(x_k)}{w_{k,i}}</tex><br>
 где <br>
@@ Строка 39: / Строка 39: @@
 <tex>P_n(x) = A_0 + A_1(x-x_0) + ...+ A_n(x - x_0)...(x - x_{n-1})</tex><br>
 Такое представление полинома удобно для вычисления, потому что увеличение числа узлов на единицу требует добавления только одного слагаемого.<br>
 ==Погрешность интерполирования==
@@ Строка 82: / Строка 80: @@
 == Литература ==
-[1]Самарский А.А. Гулин А.В. Численные методы 1989г.
+# Самарский А.А. Гулин А.В. Численные методы 1989г.
-[2]Костомаров Д.П., Фаворский А.П.  Вводные лекции по численным методам
+# Костомаров Д.П., Фаворский А.П.  Вводные лекции по численным методам
+== Смотри также ==
+* [[Практикум ММП ВМК, 4й курс, осень 2008]]
+{{stub}}
+[[Категория:Учебные задачи]]