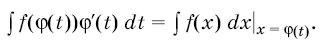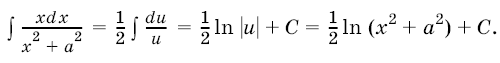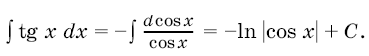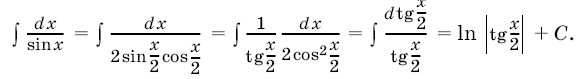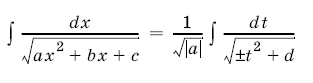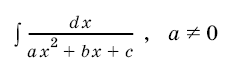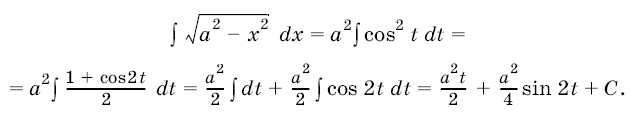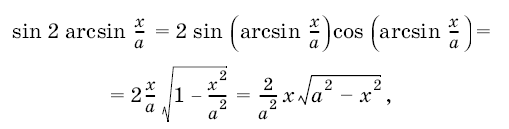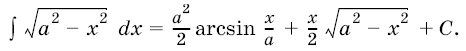Участник:Пасконова Ольга/Песочница
Материал из MachineLearning.
(→Формула замены переменных в неопределенном интеграле) |
(→Формула замены переменных в неопределенном интеграле) |
||
| Строка 54: | Строка 54: | ||
Для того чтобы существовала функция <tex> \phi^{-1} </tex>, обратная <tex> \phi </tex>, в дополнение к условиям теоремы достаточно, например, потребовать, чтобы на рассматриваемом промежутке <tex> \Delta_t </tex> функция <tex> \phi </tex> была строго монотонной. В этом случае, существует однозначная обратная функция <tex> \phi^{-1} </tex>. | Для того чтобы существовала функция <tex> \phi^{-1} </tex>, обратная <tex> \phi </tex>, в дополнение к условиям теоремы достаточно, например, потребовать, чтобы на рассматриваемом промежутке <tex> \Delta_t </tex> функция <tex> \phi </tex> была строго монотонной. В этом случае, существует однозначная обратная функция <tex> \phi^{-1} </tex>. | ||
| + | |||
| + | '''4.''' Интегралы вида [[Изображение:Q14.png]] в том случае, когда подкоренное выражение неотрицательно на некотором промежутке, легко сводятся с помощью заме¬ны переменного к табличным. | ||
| + | |||
| + | Действительно, замечая, что [[Изображение:Q15.png]], сделаем замену переменной [[Изображение:Q16.png]] и положим [[Изображение:Q17.png]]. Тогда [[Изображение:Q18.png]] и, в силу формулы {{eqref|2}}, получим | ||
| + | |||
| + | ::[[Изображение:Q19.png]] | ||
| + | |||
| + | (перед <tex> t^2 </tex> стоит знак плюс, если а > 0, и знак минус, если а < 0). Интеграл, стоящий в правой части равенства, является табличным. Найдя его по соответствующим формулам и вернувшись от переменной <tex> t </tex> к переменной <tex> x </tex>, получим искомый интеграл. | ||
| + | |||
| + | Подобным же приемом вычисляются и интегралы вида | ||
| + | |||
| + | ::[[Изображение:Q20.png]] | ||
| + | |||
| + | '''5.''' Интеграл [[Изображение:Q21.png]] можно вычислить с помощью подстановки | ||
| + | <tex> x = a sin t </tex>. Имеем <tex> dx = a cos t dt </tex>, поэтому | ||
| + | |||
| + | ::[[Изображение:Q22.png]] | ||
| + | |||
| + | Подставляя это выражение <tex> t = arcsin \frac{x}{a} </tex> и замечая, что | ||
| + | |||
| + | ::[[Изображение:Q23.png]] | ||
| + | |||
| + | окончательно будем иметь | ||
| + | |||
| + | ::[[Изображение:Q24.png]] | ||
| + | |||
| + | Заметим, что для проверки результата, полученного при вычислении неопределенного интеграла, достаточно его продифференцировать, после чего должно получиться подынтегральное выражение вычисляемого иптеграла. | ||
Версия 18:05, 16 ноября 2008
Формула замены переменных в неопределенном интеграле
Рассмотрим свойство неопределенного интеграла, часто оказывающееся полезным при вычислении первообразных элементарных функций.
Теорема.
Пусть функции и
определены соответственно на промежутках
и
, причем
. Если функция
имеет на
первообразную
и, следовательно,
(1)
а функция дифференцируема на
, то функция
имеет на
, первообразную
и
(2)
Формула (1) называется формулой интегрирования подстановкой, а именно подстановкой . Это название объясняется тем, что если формулу (2) записать в виде
то будет видно, что, для того чтобы вычислить интеграл 
), можно сделать подстановку , вычислить интеграл
и затем вернуться к переменной
, положив
.
Примеры.
1. Для вычисления интеграла естественно сделать подстановку
, тогда
2. Для вычисления интеграла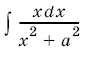 
удобно применить подстановку
:
3. При вычислении интегралов вида 
полезна подстановка
:
Например,
Иногда, прежде чем применить метод интегрирования подстановкой, приходится проделать более сложные преобразования подынтегральной функции:
Отметим, что формулу (2) бывает целесообразно использовать и в обратном порядке, т.е. справа палево. Именно, иногда удобно вычисление интеграла с помощью соответствующей замены переменного
свести к вычислению интеграла
(если этот интеграл в каком-то смысле «проще» исходного).
В случае, когда функция имеет обратную
, перейдя в обеих частях формулы (2) к переменной
с помощью подстановки
и поменяв местами стороны равенства, получим
Эта формула называется обычно формулой интегрирования заменой переменной.
Для того чтобы существовала функция , обратная
, в дополнение к условиям теоремы достаточно, например, потребовать, чтобы на рассматриваемом промежутке
функция
была строго монотонной. В этом случае, существует однозначная обратная функция
.
4. Интегралы вида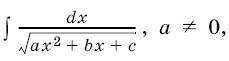 
в том случае, когда подкоренное выражение неотрицательно на некотором промежутке, легко сводятся с помощью заме¬ны переменного к табличным.
Действительно, замечая, что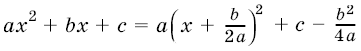 
, сделаем замену переменной 
и положим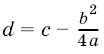 
. Тогда 
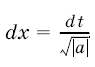и, в силу формулы (2), получим
(перед стоит знак плюс, если а > 0, и знак минус, если а < 0). Интеграл, стоящий в правой части равенства, является табличным. Найдя его по соответствующим формулам и вернувшись от переменной
к переменной
, получим искомый интеграл.
Подобным же приемом вычисляются и интегралы вида
5. Интеграл 
можно вычислить с помощью подстановки
. Имеем
, поэтому
Подставляя это выражение и замечая, что
окончательно будем иметь
Заметим, что для проверки результата, полученного при вычислении неопределенного интеграла, достаточно его продифференцировать, после чего должно получиться подынтегральное выражение вычисляемого иптеграла.
