Логистическая функция
Материал из MachineLearning.
(категория, викификация) |
|||
| Строка 1: | Строка 1: | ||
| - | + | {{TOCright}} | |
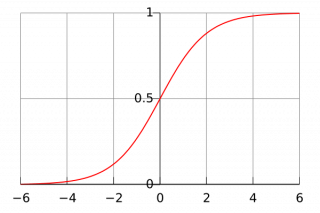
Логистическая функция или логистическая кривая - самая общая сигмоидальная (S-образная) кривая. Она моделирует кривую роста вероятности некоего события, по мере изменения управляющих параметров (факторов риска). | Логистическая функция или логистическая кривая - самая общая сигмоидальная (S-образная) кривая. Она моделирует кривую роста вероятности некоего события, по мере изменения управляющих параметров (факторов риска). | ||
| Строка 10: | Строка 10: | ||
Логистическая функция находит применение в обширном диапазоне областей знания, включая искусственные нейронные сети, биологию, биоматематику, экономику, химию, математическую психологию, вероятность и статистику. | Логистическая функция находит применение в обширном диапазоне областей знания, включая искусственные нейронные сети, биологию, биоматематику, экономику, химию, математическую психологию, вероятность и статистику. | ||
| + | |||
| + | [[Image:Logistic-curve.png|thumb|320px|right|Логистическая функция (сигмоида)]] | ||
==Логистическое дифференциальное уравнение.== | ==Логистическое дифференциальное уравнение.== | ||
| Строка 15: | Строка 17: | ||
Логистическая функция - решение простого нелинейного дифференциального уравнения первого порядка: | Логистическая функция - решение простого нелинейного дифференциального уравнения первого порядка: | ||
| - | :<tex>\frac{dP}{dt}=P(1-P) | + | :<tex>\frac{dP}{dt}=P(1-P),</tex> |
| - | + | где P – переменная, зависящая от времени t и с граничным условием P (0) = 1/2. Это уравнение - непрерывная версия логистического отображения. | |
Можно легко найти решение этого уравнения и получить две наиболее распространенных формы записи логистической зависимости после интегрирования: | Можно легко найти решение этого уравнения и получить две наиболее распространенных формы записи логистической зависимости после интегрирования: | ||
| Строка 27: | Строка 29: | ||
:<tex>2 \, P(t) = 1 + \tanh \left( \frac{t}{2} \right).</tex> | :<tex>2 \, P(t) = 1 + \tanh \left( \frac{t}{2} \right).</tex> | ||
| - | ==Двойная логистическая сигмоидальная кривая | + | ==Двойная логистическая сигмоидальная кривая== |
| - | [[Image:dsigmoid.png|200px|right|thumb| | + | [[Image:dsigmoid.png|200px|right|thumb|Двойная логистическая функция]] |
Двойной логистической является функция, подобная логистической функции с многочисленными проявлениями. Его общая формула: | Двойной логистической является функция, подобная логистической функции с многочисленными проявлениями. Его общая формула: | ||
| Строка 50: | Строка 52: | ||
* [http://8020world.com/jcmendez/2007/04/business/modeling-market-adoption-in-excel-with-a-simplified-s-curve Моделирование в Excel с упрощенной кривой s] | * [http://8020world.com/jcmendez/2007/04/business/modeling-market-adoption-in-excel-with-a-simplified-s-curve Моделирование в Excel с упрощенной кривой s] | ||
* [http://mathworld.wolfram.com/SigmoidFunction.html MathWorld: Функция Сигмоид] | * [http://mathworld.wolfram.com/SigmoidFunction.html MathWorld: Функция Сигмоид] | ||
| + | |||
| + | [[Категория:Регрессионный анализ]] | ||
Текущая версия
|
Логистическая функция или логистическая кривая - самая общая сигмоидальная (S-образная) кривая. Она моделирует кривую роста вероятности некоего события, по мере изменения управляющих параметров (факторов риска).
Вероятность P можно также трактовать как заселенность. Начальная стадия роста логистической кривой приблизительно соответствует экспоненте (показательная функция). Затем, по мере насыщения, рост замедляется, проходит линейную фазу и, наконец, и в зрелом периоде практически останавливается. Простейшая логистическая функция может быть описана формулой:
где переменную P можно рассматривать как численность населения, а переменную t – как время. Хотя область допустимых значений t совпадает со множеством всех действительных чисел от минус до плюс бесконечности, практически, из-за природы показательной функции exp(−t), достаточно вычислить значения в сравнительно узком интервале [− 6, + 6].
Логистическая функция находит применение в обширном диапазоне областей знания, включая искусственные нейронные сети, биологию, биоматематику, экономику, химию, математическую психологию, вероятность и статистику.
Логистическое дифференциальное уравнение.
Логистическая функция - решение простого нелинейного дифференциального уравнения первого порядка:
где P – переменная, зависящая от времени t и с граничным условием P (0) = 1/2. Это уравнение - непрерывная версия логистического отображения. Можно легко найти решение этого уравнения и получить две наиболее распространенных формы записи логистической зависимости после интегрирования:
или (выбирая постоянную интегрирования) :
Логистическая функция – является обратной по отношению к функции logit (с натуральным логарифмом) и так же может использоваться, чтобы преобразовать логарифм перевеса в вероятность; преобразование от отношения вероятностей регистрации двух альтернатив также принимает форму логистической кривой. Логистическая сигмоидальная функция тесно связана с гиперболическим тангенсом:
Двойная логистическая сигмоидальная кривая
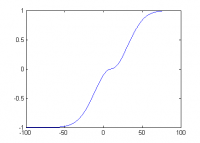
Двойной логистической является функция, подобная логистической функции с многочисленными проявлениями. Его общая формула:
где d – локальный центр, и s - фактор крутизны. Здесь "sign" представляет функцию знака. Эта кривая основана на Гауссовском распределении, и графически подобна двум идентичным логистическим сигмоидам, соединенным вместе в пункте x = d. Одно из его приложений - нелинейная нормализация выборок, использующая свойство устранения выбросов.
Так же смотри
Литература
1. Kingsland, S. E. (1995) Modeling nature ISBN 0-226-43728-0 2. Weisstein, Eric W. "Logistic Equation". From MathWorld--A Wolfram Web Resource. Retrieved on 2008-10-21.