Автокорреляционная функция
Материал из MachineLearning.
| Строка 4: | Строка 4: | ||
=== Определение === | === Определение === | ||
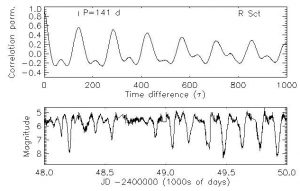
| + | [[Изображение:Autocorrelation.png|thumb|right|300px|На графиках представлена коррелограмма сигнала и собственно сигнал. Коррелограмма проявляет неочевидные периодические составляющие сигнала.]] | ||
В [[Статистика|статистике]] автокорреляция [[Случайный процесс|случайного процесса]] описывает [[корреляция|корреляцию]] между значениями процесса в различные моменты времени. Пусть <tex>X_t</tex> - значение случайного процесса в момент времени <tex>t</tex> (<tex>t</tex> может быть вещественным, если процесс непрервыный, или целым, если процесс дискретный). Если <tex>X_t</tex> имеет среднее значение <tex>\mu_t</tex> и дисперсию <tex>\omega _t^2</tex>, то автокорреляция <tex>X_t</tex> определяется следующим образом: | В [[Статистика|статистике]] автокорреляция [[Случайный процесс|случайного процесса]] описывает [[корреляция|корреляцию]] между значениями процесса в различные моменты времени. Пусть <tex>X_t</tex> - значение случайного процесса в момент времени <tex>t</tex> (<tex>t</tex> может быть вещественным, если процесс непрервыный, или целым, если процесс дискретный). Если <tex>X_t</tex> имеет среднее значение <tex>\mu_t</tex> и дисперсию <tex>\omega _t^2</tex>, то автокорреляция <tex>X_t</tex> определяется следующим образом: | ||
| Строка 21: | Строка 22: | ||
График автокорреляций выборки в зависиости от сдвига называется [[Коррелограмма|коррелограммой]]. | График автокорреляций выборки в зависиости от сдвига называется [[Коррелограмма|коррелограммой]]. | ||
| + | |||
| + | == Свойства == | ||
Версия 14:31, 10 января 2009
Автокорреляционная функция - это характеристика сигнала, которая помогает находить повторяющиеся участки сигнала или определять несущую частоту сигнала, скрытую из-за наложений шума и колебаний на других частотах. Автокорреляционная функция часто используется в обработке сигналов и анализе временных рядов.
Неформально автокорреляционная функция - это сходство между значениями сигнала как функция от разницы во времени между ними.
Определение
В статистике автокорреляция случайного процесса описывает корреляцию между значениями процесса в различные моменты времени. Пусть - значение случайного процесса в момент времени
(
может быть вещественным, если процесс непрервыный, или целым, если процесс дискретный). Если
имеет среднее значение
и дисперсию
, то автокорреляция
определяется следующим образом:
,
где "E" - это математическое ожидание. Заметим, что это определение не всегда корректно, так как знаменятель дроби может обращаться в нуль (для процессов-констант) или в бесконечность. Если же это выражение корректно, то его значение лежит в интервале [−1, 1], причем 1 оно принимает в случае полного совпадения, а −1 - в случае, если корреляции не наблюдается.
Для дискретного процесса длиной n с известными матожиданием и дисперсией автокорреляцию можно рассчитывать по следующей формуле:
для любых положительных целых k и n.
График автокорреляций выборки в зависиости от сдвига называется коррелограммой.