EM-алгоритм с последовательным добавлением компонент (пример)
Материал из MachineLearning.
(→Вычислительный эксперимент) |
(→Вычислительный эксперимент) |
||
| Строка 75: | Строка 75: | ||
*В качестве второго примера возьмем 2 плохо разделимых класса. | *В качестве второго примера возьмем 2 плохо разделимых класса. | ||
| + | |||
[[Изображение:twobadclasses.png|400px]] | [[Изображение:twobadclasses.png|400px]] | ||
| Строка 83: | Строка 84: | ||
*Реальные данные | *Реальные данные | ||
| - | Проверку алгоритма проведем на классической задаче: Ирисы Фишера | + | <source lang="matlab"> |
| - | Объектами являются 3 типа ирисов: setosa, versicolor, virginica | + | load 'iris2.data' |
| + | X = iris2(:,[3,4]); | ||
| + | Y = [ones([50,1]);2*ones([50,1]);3*ones([50,1])]; | ||
| + | hold off | ||
| + | drawdata(X,Y,'*'); | ||
| + | title('Irises classification') | ||
| + | xlabel('petal width, cm'); | ||
| + | ylabel('petal length, cm'); | ||
| + | legend('Iris Setosa','Iris Versicolour','Iris Virginica','Location','NorthWest'); | ||
| + | [W,M,Sigma,k,Ytheta] = emlearn(X, Y, [2,20,0.0005]) | ||
| + | [Yanswer] = emtest(X, M, Sigma, Ytheta); | ||
| + | drawdata(X,Yanswer,'o') | ||
| + | </source> | ||
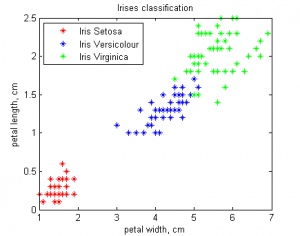
| + | Проверку алгоритма проведем на классической задаче: [http://archive.ics.uci.edu/ml/datasets/Iris Ирисы Фишера] | ||
| + | Объектами являются 3 типа ирисов: [http://ru.wikipedia.org/wiki/%D0%98%D1%80%D0%B8%D1%81_%D1%89%D0%B5%D1%82%D0%B8%D0%BD%D0%B8%D1%81%D1%82%D1%8B%D0%B9 setosa], [http://en.wikipedia.org/wiki/Iris_versicolor versicolor], virginica | ||
[[Изображение:setosa.jpg|275px]] | [[Изображение:setosa.jpg|275px]] | ||
| Строка 97: | Строка 112: | ||
[[Изображение:Ireses_sorted¢ers.png|300px]] | [[Изображение:Ireses_sorted¢ers.png|300px]] | ||
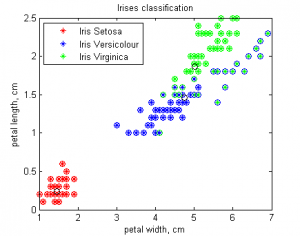
| - | Алгоритм хорошо отделил ирисы setosa от остальных, но допустил достаточное число ошибок при разделении ирисов versicolor и virginica. Это произошло потому, что алгоритм изначально решал задачу кластеризации и лишь потом задачу классификации, приписывая каждому кластеру номер наиболее хорошо приближаемого им класса. Для отделения последних двух классов можно использовать | + | Алгоритм хорошо отделил ирисы setosa от остальных, но допустил достаточное число ошибок при разделении ирисов versicolor и virginica. Это произошло потому, что алгоритм изначально решал задачу кластеризации и лишь потом задачу классификации, приписывая каждому кластеру номер наиболее хорошо приближаемого им класса. Для отделения последних двух классов можно использовать [[Линейный классификатор | Линейные алгоритмы классификации]], либо решать с помощью [[EM алгоритм (пример) | EM]], но используя все 4 признака. |
== Исходный код == | == Исходный код == | ||
Версия 14:16, 2 мая 2009
|
EM-алгоритм с последовательным добавлением компонент (пример) — общий метод нахождения функции плотности распределения объектов. Предполагается, что она имеет вид смеси распределений.
В данной статье рассматривается гауссовское распредение выборки, количество гауссианов произвольно.
Постановка задачи
Задана выборка , в которой
=
- множество объектов,
=
- множество ответов. Предполагается, что объекты имеют плотность распределения
, представимую в виде смеси
гауссиан с параметрами
и
.
Задача разделения смеси заключается в том, чтобы, имея выборку случайных и независимых наблюдений из смеси
оценить вектор параметров
доставляющий максимум функции правдоподобия
Алгоритм отыскания оптимальных параметров
Оптимальные параметры отыскиваются последовательно с помощью EM-алгоритма. Идея заключается во введении вспомогательного вектора скрытых переменных , обладающего двумя замечательными свойствами. С одной стороны, он может быть вычислен, если известны значения вектора параметров
, с другой стороны, поиск максимума правдоподобия сильно упрощается, если известны значения скрытых переменных.
EM-алгоритм состоит из итерационного повторения двух шагов. На E-шаге вы-
числяется ожидаемое значение (expectation) вектора скрытых переменных
по те-
кущему приближению вектора параметров
. На М-шаге решается задача максими-
зации правдоподобия (maximization) и находится следующее приближение вектора
по текущим значениям векторов
и
.
Если число компонент смеси заранее не известно, то применяется EM-алгоритм с последовательным добавлением компонент. Если при каком-либо
число неправильно классифицированных объектов превышает допустимое, то
увеличивается и повторяется EM(
)
- Вход:
Выборка ;
- максимальный допустимый разброс правдоподобия объектов;
- минимальная длина выборки, по которой можно восстановить плотность;
- параметр критерия останова;
- Выход:
- число компонент смеси;
- Алгоритм
1. начальное приближение - одна компонента:
2. для всех
3. выделить объекты с низким правдоподобием
4. Если то выход из цикла по
5. Начальное приближение для компоненты:
6.
Вычислительный эксперимент
Алгоритм тестируется на модельных и реальных данных
- Рассмотрим пример модельных данных. Выборка состоит из 4 классов. Первый класс представляет собой две гауссианы с диагональной и недиагоныльной матрицами ковариации, остальные - одна гауссиана.
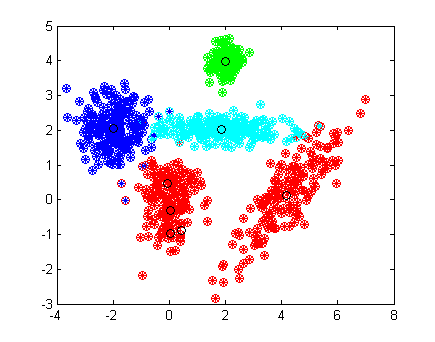
[X1, Y1] = gengaussdata(150, [0;0], [1/4,1/2]); [X2, Y2] = gengaussdata(150, [4;0], [1 5/6;5/6 1]); [X4, Y4] = gengaussdata(120, [2;4], [1/10;1/10]); [X3, Y3] = gengaussdata(200, [-2,2], [1/3, 1/3]); [X5, Y5] = gengaussdata(200, [2,2], [1.25, 1/20]); X=[X1;X2;X3;X4;X5]; %Y are answers (numbers of classes) Y=[Y1;Y2;Y3+1;Y4+2;Y5+3]; hold off drawdata(X,Y,'*'); %learning algorithm [W,M,Sigma,k,Ytheta] = emlearn(X, Y, [2,40,0.001]) %testing and geting answers from algorithm [Yanswer] = emtest(X, M, Sigma, Ytheta); drawdata(X,Yanswer,'o'); %printing centers of classes according to algorithm decision printcenters(M);
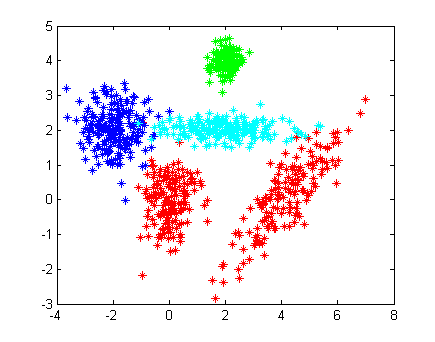
Истинное распределение классов показано на рисунке слева. Одинаковым цветом помечены элементы одного класса. Как можно заметить, некоторые представители "красныйх", "бирюзовых" и "синих" перемешались.
Качество обучения алгоритма проверяется на той же выборке. На правом рисунке кружками показаны полученные ответы, цвет отвечает за принадлежность к соответствующему классу. Центры классов, отмечены черным кружками. Алгоритм нашел восемь гауссовских распределений вместо четырех, причем одна из красных компонент описывается сразу 4 гауссианами, в то время как остальные компоненты выборки - одной. Этот факт говорит о том, что одна гауссиана плохо приближает данное распределение, и, для уменьшениея числа ошибок, следует приблизить её большим числом гауссиан. Алгоритм допустил 16 ошибок, что на выборке из 820 элементов составляет менее 2%.
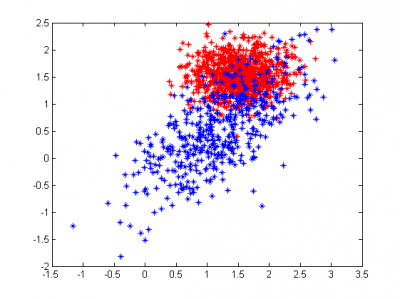
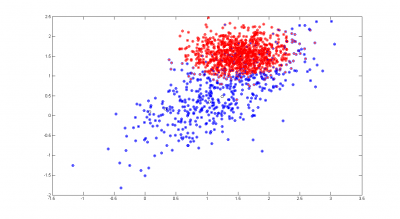
- В качестве второго примера возьмем 2 плохо разделимых класса.
Благодаря тому, что алгоритм выделил 4 гауссианы в синем классе, некоторые его элементы, далеко забравшиеся в чужой класс, были классифицированы правильно.
- Реальные данные
load 'iris2.data' X = iris2(:,[3,4]); Y = [ones([50,1]);2*ones([50,1]);3*ones([50,1])]; hold off drawdata(X,Y,'*'); title('Irises classification') xlabel('petal width, cm'); ylabel('petal length, cm'); legend('Iris Setosa','Iris Versicolour','Iris Virginica','Location','NorthWest'); [W,M,Sigma,k,Ytheta] = emlearn(X, Y, [2,20,0.0005]) [Yanswer] = emtest(X, M, Sigma, Ytheta); drawdata(X,Yanswer,'o')
Проверку алгоритма проведем на классической задаче: Ирисы Фишера Объектами являются 3 типа ирисов: setosa, versicolor, virginica
У каждого объекта есть 4 признака: длина лепестка, ширина лепестка, длина чашелистика, ширина чашелистика
Для удобства изображения результатов будем использовать первые два признака.
Алгоритм хорошо отделил ирисы setosa от остальных, но допустил достаточное число ошибок при разделении ирисов versicolor и virginica. Это произошло потому, что алгоритм изначально решал задачу кластеризации и лишь потом задачу классификации, приписывая каждому кластеру номер наиболее хорошо приближаемого им класса. Для отделения последних двух классов можно использовать Линейные алгоритмы классификации, либо решать с помощью EM, но используя все 4 признака.
Исходный код
Скачать листинги алгоритмов можно здесь EMk.m, emlearn.m, emtest.m
Смотри также
Литература
- К. В. Воронцов, Лекции по статистическим (байесовским) алгоритмам классификации
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |