Статистический анализ данных (курс лекций, К.В.Воронцов)/2009

Материал из MachineLearning.

(Различия между версиями)

Версия 17:43, 24 сентября 2009

Содержание

1 Задание 1
- 1.1 Пример выполнения задания
- 1.2 Индивидуальные параметры задания

Задание 1

Необходимо провести исследование одного из классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо сгенерировать одну или несколько выборок из указанного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. При этом, в зависимости от индивидуальных особенностей задания, выборки могут как генерироваться заново для каждого значения объёма выборки $n$ , так и образовываться путём добавления одного элемента к уже имеющейся выборке объёма $n-1$ . По результатам расчётов необходимо построить следующие графики:

график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента (1 балл);
график зависимости достигаемого уровня значимости от значений параметров, усреднённого по нескольким десяткам экспериментов (+1 балл);
график с эмпирическими оценками мощности критерия для разных значений параметров (+1 балл).

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся $k$ раз для каждого набора значений параметра, и в $m$ из $k$ случаев гипотеза была отвергнута на некотором фиксированном уровне значимости $\alpha$ (примем $\alpha=0.05$ ), оценкой мощности будет отношение $m/k$ .

Пример выполнения задания

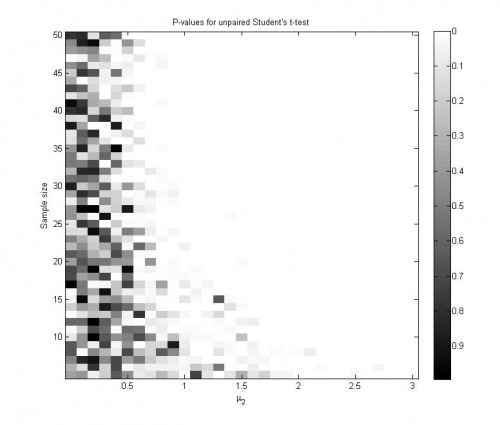
Исследуем поведение классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига. $x^n = (x_1,\ldots,x_n)\sim N(\mu_1,\sigma),\;\; y^n = (y_1,\ldots,y_n)\sim N(\mu_2,\sigma);$

$H_0\,:\; \mu_1=\mu_2,$

$H_1\,:\; \mu_1\neq\mu_2.$

Параметры задачи принимают следующие значения:

$\sigma = 1; \;\;\; \mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

График значений достигаемого уровня значимости при однократной генерации выборок:

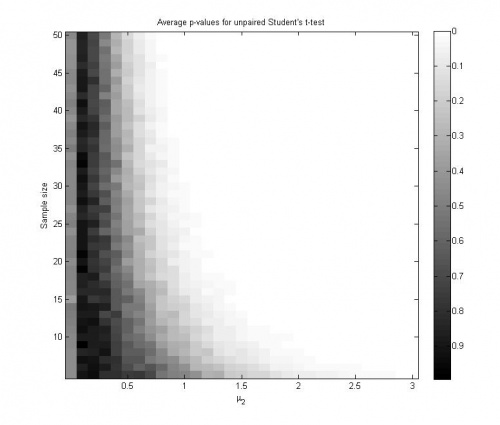
График значений достигаемого уровня значимости, усрёднённых по 100 экспериментам:

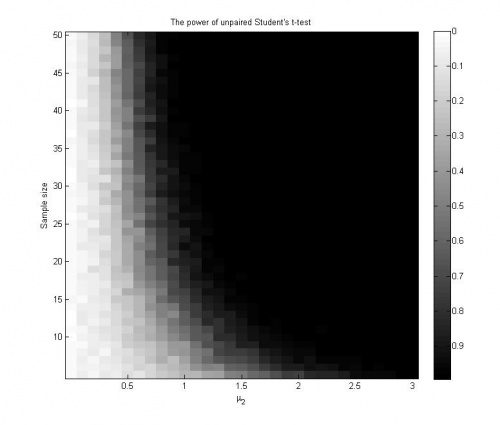
График значений эмпирических оценок мощности критерия при проведении 100 экспериментов:

Индивидуальные параметры задания

Одновыборочный критерий Стьюдента

$x^n \sim N(\mu,1);$

$H_0\,:\; \mu=0, \;\; H_1\,:\; \mu\neq 0.$

$\mu=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

Безродный Богдан

При каждом значении $\mu$ выборки для разных значений $n$ генерируются независимо.

Двойнев Александр

При каждом значении $\mu$ выборка $x^n$ получается из $x^{n-1}$ добавлением одного случайного элемента.

Двухвыборочный критерий Стьюдента для независимых выборок

$x^n \sim N(\mu_1,\sigma_1),\;\; y^n \sim N(\mu_2,\sigma_2);$

$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2.$

$n=5\,:\,1\,:\,50.$

Коликова Екатерина

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; \sigma_1=\sigma_2=1;$ при каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Задонский Дмитрий

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; \sigma_1=1;\;\;\sigma_2=2;$ при каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Ломакин Василий

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; \sigma_1=1;\;\;\sigma_2=2;$ при каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Гуков Алексей

$\mu_1=\mu_2=0; \;\;\; \sigma_1=1;\;\;\sigma_2=0.1\,:\,0.1\,:\,4;$ при каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Решетняк Илья

$\mu_1=\mu_2=0; \;\;\; \sigma_1=1;\;\;\sigma_2=0.1\,:\,0.1\,:\,4;$ при каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Двухвыборочный критерий Стьюдента для связных выборок (случай парных повторных наблюдений)

$x^n \sim N(\mu_1,1),\;\; y^n \sim N(\mu_2,1);$

$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2.$

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

Дзыба Дмитрий

При каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Осокин Антон

При каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Одновыборочный критерий Уилкоксона

$x^n \sim N(\mu,1);$

$H_0\,:\; \mu=0, \;\; H_1\,:\; \mu\neq 0.$

$\mu=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

Задонский Максим

При каждом значении $\mu$ выборки для разных значений $n$ генерируются независимо.

Карпинская Алина

При каждом значении $\mu$ выборка $x^n$ получается из $x^{n-1}$ добавлением одного случайного элемента.

Двухвыборочный критерий Уилкоксона для связных выборок (случай парных повторных наблюдений)

$x^n \sim F(\mu_1),\;\; y^n \sim F(\mu_2);$

$H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2.$

$\mu_1=0; \;\;\; \mu_2=0\,:\,0,05\,:\,3; \;\;\; n=5\,:\,1\,:\,50.$

Гикал Александр

$F=N(\mu,1);$ при каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Ломакина-Румянцева Екатерина

$F=N(\mu,1);$ при каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Джумабекова Айнагуль

$F=U[0,\mu+1];$ при каждом значении $\mu_2$ выборки для разных значений $n$ генерируются независимо.

Мягков Артем

$F=U[0,\mu+1];$ при каждом значении $\mu_2$ выборки $x^n, y^n$ получаются из $x^{n-1}, y^{n-1}$ добавлением одного случайного элемента.

Критерий Колмогорова-Смирнова для проверки нормальности

$x^n$ - смесь распределений $N(0,1)$ и $U[-a,a]$ с весами $\alpha$ и $1-\alpha$ соответственно (т.е. доли распределений в выборке равны $\alpha$ и $1-\alpha$ ).

$H_0\,:\; x^n\sim \cdot N(0,1), \;\; H_1\,:\; F_n(x)\neq N(0,1).$

$\alpha=0\,:\,0,02\,:\,1; \;\;\; n=5\,:\,1\,:\,50.$

Алимбаев Данияр

$a=1.$

Янгиров Ильдар

$a=2.$

Аманжолов Рустем

Ахламченкова Ольга

Вишняков Святослав

Голодов Валентин

Гордеев Дмитрий

Дерябин Василий

Найденов Никита

Нарышкин Андрей

Одинокова Евгения

Пасконова Ольга

Толстихин Илья

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29/2009»

@@ Строка 92: / Строка 92: @@
 ===Двухвыборочный критерий Уилкоксона для связных выборок (случай парных повторных наблюдений)===
-<tex>x^n \sim N(\mu_1,1),\;\; y^n \sim N(\mu_2,1);</tex>
+<tex>x^n \sim F(\mu_1),\;\; y^n \sim F(\mu_2);</tex>
 <tex>H_0\,:\; \mu_1=\mu_2, \;\; H_1\,:\; \mu_1\neq\mu_2.</tex>
@@ Строка 99: / Строка 99: @@
 =====Гикал Александр=====
-При каждом значении <tex>\mu_2</tex> выборки для разных значений <tex>n</tex> генерируются независимо.
+<tex>F=N(\mu,1);</tex> при каждом значении <tex>\mu_2</tex> выборки для разных значений <tex>n</tex> генерируются независимо.
 =====Ломакина-Румянцева Екатерина=====
-При каждом значении <tex>\mu_2</tex> выборки <tex>x^n, y^n</tex> получаются из <tex>x^{n-1}, y^{n-1}</tex> добавлением одного случайного элемента.
+<tex>F=N(\mu,1);</tex> при каждом значении <tex>\mu_2</tex> выборки <tex>x^n, y^n</tex> получаются из <tex>x^{n-1}, y^{n-1}</tex> добавлением одного случайного элемента.
+=====Джумабекова Айнагуль=====
+<tex>F=U[0,\mu+1];</tex> при каждом значении <tex>\mu_2</tex> выборки для разных значений <tex>n</tex> генерируются независимо.
+=====Мягков Артем=====
+<tex>F=U[0,\mu+1];</tex> при каждом значении <tex>\mu_2</tex> выборки <tex>x^n, y^n</tex> получаются из <tex>x^{n-1}, y^{n-1}</tex> добавлением одного случайного элемента.
 ===Критерий Колмогорова-Смирнова для проверки нормальности===
@@ Строка 117: / Строка 121: @@
 =====Аманжолов Рустем=====
 =====Ахламченкова Ольга=====
 =====Вишняков Святослав=====
 =====Голодов Валентин=====
 =====Гордеев Дмитрий=====
 =====Дерябин Василий=====
-=====Джумабекова Айнагуль=====
-=====Мягков Артем=====
 =====Найденов Никита=====
 =====Нарышкин Андрей=====
 =====Одинокова Евгения=====
 =====Пасконова Ольга=====
 =====Толстихин Илья=====

Статистический анализ данных (курс лекций, К.В.Воронцов)/2009

Материал из MachineLearning.

Версия 17:43, 24 сентября 2009

Содержание

Задание 1

Пример выполнения задания

Индивидуальные параметры задания

Одновыборочный критерий Стьюдента

Безродный Богдан

Двойнев Александр

Двухвыборочный критерий Стьюдента для независимых выборок

Коликова Екатерина

Задонский Дмитрий

Ломакин Василий

Гуков Алексей

Решетняк Илья

Двухвыборочный критерий Стьюдента для связных выборок (случай парных повторных наблюдений)

Дзыба Дмитрий

Осокин Антон

Одновыборочный критерий Уилкоксона

Задонский Максим

Карпинская Алина

Двухвыборочный критерий Уилкоксона для связных выборок (случай парных повторных наблюдений)

Гикал Александр

Ломакина-Румянцева Екатерина

Джумабекова Айнагуль

Мягков Артем

Критерий Колмогорова-Смирнова для проверки нормальности

Алимбаев Данияр

Янгиров Ильдар

Аманжолов Рустем

Ахламченкова Ольга

Вишняков Святослав

Голодов Валентин

Гордеев Дмитрий

Дерябин Василий

Найденов Никита

Нарышкин Андрей

Одинокова Евгения

Пасконова Ольга

Толстихин Илья

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты