Непараметрическая регрессия: ядерное сглаживание

Материал из MachineLearning.

(Различия между версиями)

Перейти к: навигация, поиск

Версия 17:36, 3 января 2010

Статья плохо доработана.

Имеются указания по её улучшению:

Ядерное сглаживание - один из простейших видов непараметрической регрессии.

Содержание

1 Принцип
2 Описание метода
3 Литература
4 См. также

Принцип

Принцип, используйщий идейно простой подход к представлению последовательности весов $\{ W_{ni}(x) \}_{i=1}^n$ состоит в описании формы весовой функции $W_{ni}(x)$ посредством функции плотности со скалярным параметром, который регулирует размер и форму весов около х. Эту функцию формы принято называть ядром $K$ .

Описание метода

Определение ядра

Ядро — это непрерывная ограниченная симметричная вещественная функция $K$ с единичным интегралом

$\int K(u)du=1$

Последовательность весов

Последовательность весов для ядерных оценок (для одномерного $x$ ) определяется как :: $W_{ni}(x)=\frac{K_{h_n}(x\;-\;X_i)}{\hat{f}_{h_n}(x)}$ , где

$\hat{f}_{h_n}(x)=\frac{\sum_{i=1}^n K_{h_n}(x\;-\;X_i)}{n}$ ,

$K_{h_n}(u)=\frac{K$\frac{u}{h_n}$}{h_n}$

представляет собой ядро с параметром $h_n$ . Этот параметр принято называть шириной окна. Подчеркнув зависимость $h\ =\ h_n$ от объема выборки $n$ , условимся сокращенно обозначать последовательность весов $W_{ni}(x)$ .

Функция ядра

Функция $\hat{f}_{h_n}(x)$ является ядерной оценкой плотности Розенблата — Парзена (Rosenblatt, 1956; Parzen, 1962) для (маргинальной) плотности переменной $x$ . Данный вид ядерных весов $W_{ni}(x)$ был предложен в работах (Nadaraya, 1964) и (Watson, 1964), и, как следствие,

$\hat{m}_h(x)=\frac{n^{-1}\sum_{i=1}^n K_{h_n}(x\;-\;X_i)Y_i}{n^{-1}\sum_{i=1}^n K_{h_n}(x\;-\;X_i)}$

часто называют оценкой Надарая — Ватсона. форма ядерных весов определяется ядром $K$ в то время как размер весов параметризируется посредством переменной $h$ , называемой шириной окна. Нормализация весов $\hat{f}_{h_n}(x)$ позволяет адаптироваться к локальной интенсивности переменной $x$ и, кроме того, гарантирует, что сумма весов равна еденице. Вообще говоря, можно брать различные ядерные функции, но как практика, так и теория ограничивают выбор. Так, например, ядерные функции, принимающие очень малые значения, могут приводить к машинному нулю компьютера, поэтому разумно рассматривать такие ядерные функции, которые равны нулю вне некоторого фиксированного интервала.

Пример функции ядра

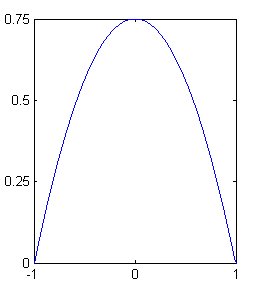
Ядро Бпанечникова. Это ядро имеет параболическую форму и носитель .

Ядро Бпанечникова. Это ядро $K(u)=0.75(1-u^2)I(\| u \| \le 1)$ имеет параболическую форму и носитель $[-1,1]$ .

Обычно используется ядерная функция, обладающая некоторыми свойствами оптимальности [Хардле В п4.5]; это функция параболического типа (Epanechnikov, 1969; Bartlett, 1963):

$K(u)=0.75(1-u^2)I(\| u \| \le 1)$ .

Замечание. Ядро не дифференцируемо при $u = \pm 1$ . Ядерная оценка не определена для значения ширины окна с $\hat{f}_{h_n}(x)=0$ . Если такой случай $0/0$ возникает, то $\hat{m}_h(x)$ определяется как $0$ .

Зависимость от ширины окна

Допустим, что ядерная оценка вычисляется только в точках наблюдений $\{ X_i\}_{i=1}^n$ . Тогда при $h\rightarrow0$ ,

$\hat{m}_h(x)\rightarrow\frac{K(0)Y_i}{K(0)}=Y_i$ ;

следовательно, малая ширина окна воспроизводит данные. Исследуем теперь, что происходит при $h\rightarrow\infty$ . Допустим, что $K$ имеет носитель $[-1,1]$ , как на рис. Тогда $K(x\;-\;X_i/h)\rightarrow K(0)$ и, следовательно,

$\hat{m}_h(x)=\frac{n^{-1}\sum_{i=1}^n K(0)Y_i}{n^{-1}\sum_{i=1}^n K(0)}\;=\;n^{-1}\sum_{i=1}^n Y_i$

Слишком большое значение ширины окна приводит, таким образом, к чрезмерному сглаживанию кривой — среднему арифметическому значений переменной отклика. Осюда можно сделать вывод, что актуальность сглаживания зависит от выбора ширины окна. На практике, выбор ширины окна зачастую является более важной пролемой, чем выбор самого ядра.

Литература

Хардле В. Прикладная непараметрическая регрессия. — 1989.
Воронцов К.В. Лекции по алгоритмам восстановления регрессии. — 2007.

См. также

Данная статья является непроверенным учебным заданием.

Студент: Участник:Tolstikhin

Преподаватель: Участник:Vokov

Срок: 31 декабря 2009

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9D%D0%B5%D0%BF%D0%B0%D1%80%D0%B0%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F:_%D1%8F%D0%B4%D0%B5%D1%80%D0%BD%D0%BE%D0%B5_%D1%81%D0%B3%D0%BB%D0%B0%D0%B6%D0%B8%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5»

Категории: Регрессионный анализ | Непроверенные учебные задания

@@ Строка 20: / Строка 20: @@
 a
 ::<tex>K_{h_n}(u)=\frac{K\(\frac{u}{h_n}\)}{h_n}</tex>
-представляет собой ядро с параметром масштаба <tex>h_n</tex>. Подчеркнув зависимость <tex>h\ =\ h_n</tex> от объема выборки <tex>n</tex>, условимся сокращенно обозначать последовательность весов <tex>W_{ni}(x)</tex>.
+представляет собой ядро с параметром <tex>h_n</tex>. Этот параметр принято называть шириной окна. Подчеркнув зависимость <tex>h\ =\ h_n</tex> от объема выборки <tex>n</tex>, условимся сокращенно обозначать последовательность весов <tex>W_{ni}(x)</tex>.
 === Функция ядра ===