Участник:Platonova.Elena/Песочница
Материал из MachineLearning.
| Строка 83: | Строка 83: | ||
=Примеры работы= | =Примеры работы= | ||
==Пример работы №1== | ==Пример работы №1== | ||
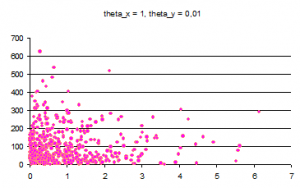
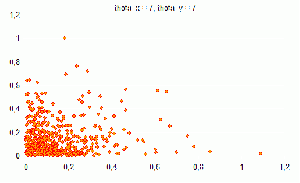
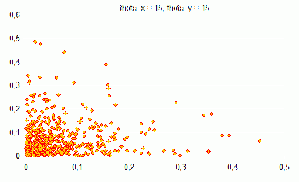
| - | Смесь из двух компонент | + | Смесь из двух компонент по 500 элементов |
[[Изображение:1,_001.png|300px|Распределение theta_x=1 theta_y=0,01]] | [[Изображение:1,_001.png|300px|Распределение theta_x=1 theta_y=0,01]] | ||
| Строка 92: | Строка 92: | ||
'''Количество ошибок при классификации:''' | '''Количество ошибок при классификации:''' | ||
| - | ''ЕМ'' 1 из 500 (2%) | + | ''ЕМ'' 1 из 500 (0.2%) |
''k-means (k=1)'' 0 из 500 | ''k-means (k=1)'' 0 из 500 | ||
| Строка 98: | Строка 98: | ||
''k-means (k=5)'' 0 из 500 | ''k-means (k=5)'' 0 из 500 | ||
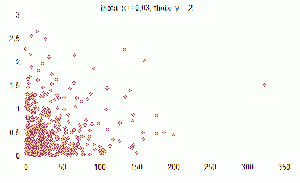
| + | ==Пример работы №2== | ||
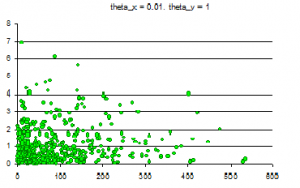
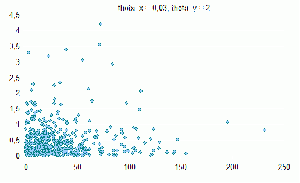
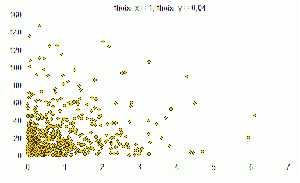
| + | Смесь из трех компонент по 500 элементов | ||
| + | [[Изображение:Image006.gif|300px|Распределение theta_x=0,03 theta_y=2]] | ||
| + | [[Изображение:Image007.gif|300px|Распределение theta_x=1 theta_y=0,04]] | ||
| + | [[Изображение:Image008.gif|300px|Распределение theta_x=7 theta_y=7]] | ||
| + | В результате работы ЕМ-алгоритма с последовательным добавлением компонент с параметрами R = 30, M = 40, Delta = 0,001 восстанавливается | ||
| + | |||
| + | <tex>\theta_1 = (0.0309435, 2.05189)</tex>, | ||
| + | |||
| + | <tex>\theta_2=(1.05747, 0.0394895)</tex>, | ||
| + | |||
| + | <tex>\theta_3=(6.56629, 6.79212)</tex> | ||
| + | |||
| + | '''Количество ошибок при классификации:''' | ||
| + | |||
| + | ''ЕМ'' 6 из 500 (1.2%) | ||
| + | |||
| + | ''k-means (k=1)'' 12 из 500 (2.2%) | ||
| + | |||
| + | ''k-means (k=5)'' 4 из 500 (0.8%) | ||
| + | |||
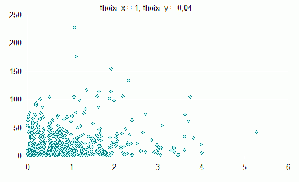
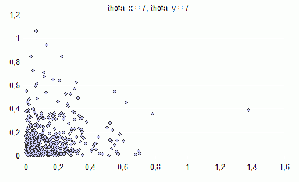
| + | ==Пример работы №3== | ||
| + | Смесь из четырех компонент по 500 элементов | ||
| + | |||
| + | [[Изображение:Image010.gif|300px|Распределение theta_x=0,03 theta_y=2]] | ||
| + | [[Изображение:Image013.gif|300px|Распределение theta_x=1 theta_y=0,04]] | ||
| + | [[Изображение:Image011.gif|300px|Распределение theta_x=7 theta_y=7]] | ||
| + | [[Изображение:Image012.gif|300px|Распределение theta_x=15 theta_y=15]] | ||
| + | |||
| + | В результате работы ЕМ-алгоритма с последовательным добавлением компонент с параметрами R = 30, M = 40, Delta = 0,001 восстанавливается | ||
| + | |||
| + | <tex>\theta_1 = (0.0300939, 1.96699)</tex>, | ||
| + | |||
| + | <tex>\theta_2=(1.02279, 0.041855)</tex>, | ||
| + | |||
| + | <tex>\theta_3=(6.1976, 6.23407)</tex>, | ||
| + | |||
| + | <tex>\theta_4=(14.8266, 12.9193)</tex> | ||
| + | |||
| + | '''Количество ошибок при классификации:''' | ||
| + | |||
| + | ''ЕМ'' 37 из 500 (7.4%) | ||
| + | |||
| + | ''k-means (k=1)'' 9 из 500 (1.8%) | ||
| + | |||
| + | ''k-means (k=5)'' 6 из 500 (1.2%) | ||
{{Задание|Platonova.Elena|Константин Воронцов|6 января 2010}} | {{Задание|Platonova.Elena|Константин Воронцов|6 января 2010}} | ||
Версия 13:27, 4 января 2010
Сравнение работы ЕМ-алгоритма и k-means для смесей с экспоненциальным распределением компонент. (будет в заголовке)
В статье приведены примеры классификации ЕМ-алгоритмом и методом k ближайших соседей двумерной смеси, компоненты которой имеют экспоненциальное распределение.
Содержание |
Краткое описание исследуемых алгоритмов
ЕМ алгоритм
Основа EM-алгоритма - предположение, что исследуемое множество данных может быть представлено с помощью линейной комбинации распределений, а цель - оценка параметров распределения, которые максимизируют логарифмическую функцию правдоподобия, используемую в качестве меры качества модели.
Пусть рассматривается смесь из распределений, каждое описывается функцией правдоподобия
- априорная вероятность
-й компоненты. Функции правдоподобия принадлежат параметрическому семейству распределений
и отличаются только значениями параметра
Вывод формул для алгоритма
Вход:
– общая длина выборки
Выход:
параметры распределения и весы компонент.
Оценка максимального правдоподобия (ОМП) θ
для одно- и двумерного случая экспоненциального распределения.
Необходимо максимизировать
Из Лагранжиана следует:
j=1,...,k
j=1,...,k.
С учетом получаем ОМП
для экспоненциального закона:
В одномерном случае:
В двумерном случае:
k-means (k ближайших соседей)
Метод ближайших соседей - это метрический алгоритм классификации, основанный на оценивании сходства объектов. Классифицируемый объект относится к тому классу, которому принадлежат ближайшие к нему объекты обучающей выборки.
Постановка задачи
Пусть - множество объектов;
- множество допустимых ответов. Задана обучающая выборка
. Задано множество объектов
.
Требуется найти множество ответов
для объектов
.
На множестве объектов задается некоторая функция расстояния, в данном случае - максимум модулей
Для произвольного объекта расположим
объекты обучающей выборки
в порядке возрастания расстояний до
:
где через обозначается
тот объект обучающей выборки, который является
-м соседом объекта
.
Аналогично для ответа на
-м соседе:
.
Таким образом, произвольный объект порождает свою перенумерацию выборки.
В наиболее общем виде алгоритм ближайших соседей есть
где — заданная весовая функция,
которая оценивает степень важности
-го соседа для классификации объекта
.
В рассматриваемом примере что соответствует методу
ближайших соседей.
Примеры работы
Пример работы №1
Смесь из двух компонент по 500 элементов
В результате работы ЕМ-алгоритма с последовательным добавлением компонент с параметрами R = 30, M = 20, Delta = 0,001 восстанавливается ,
Количество ошибок при классификации:
ЕМ 1 из 500 (0.2%)
k-means (k=1) 0 из 500
k-means (k=5) 0 из 500
Пример работы №2
Смесь из трех компонент по 500 элементов
В результате работы ЕМ-алгоритма с последовательным добавлением компонент с параметрами R = 30, M = 40, Delta = 0,001 восстанавливается
,
,
Количество ошибок при классификации:
ЕМ 6 из 500 (1.2%)
k-means (k=1) 12 из 500 (2.2%)
k-means (k=5) 4 из 500 (0.8%)
Пример работы №3
Смесь из четырех компонент по 500 элементов
В результате работы ЕМ-алгоритма с последовательным добавлением компонент с параметрами R = 30, M = 40, Delta = 0,001 восстанавливается
,
,
,
Количество ошибок при классификации:
ЕМ 37 из 500 (7.4%)
k-means (k=1) 9 из 500 (1.8%)
k-means (k=5) 6 из 500 (1.2%)
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |