Муравьиные алгоритмы
Материал из MachineLearning.
| Строка 1: | Строка 1: | ||
| + | {{TOCright}} | ||
Муравьиные алгоритмы серьезно исследуются европейскими учеными с середины 90-х годов. | Муравьиные алгоритмы серьезно исследуются европейскими учеными с середины 90-х годов. | ||
На сегодня уже получены хорошие результаты муравьиной оптимизации таких сложных комбинаторных задач, | На сегодня уже получены хорошие результаты муравьиной оптимизации таких сложных комбинаторных задач, | ||
| Строка 60: | Строка 61: | ||
#Дополнительные действия | #Дополнительные действия | ||
#* Обычно здесь используется алгоритм локального поиска, однако он может также появиться и после поиска всех решений. | #* Обычно здесь используется алгоритм локального поиска, однако он может также появиться и после поиска всех решений. | ||
| + | |||
| + | =Результаты экспериментов= | ||
| + | |||
| + | По сравнению с точными методами, например динамическим программированием или методом ветвей и границ, муравьиный алгоритм находит близкие к оптимуму решения за значительно меньшее время даже для задач большой размерности (n > 20) Время оптимизации муравьиным алгоритмом является полиномиальной функцией от размерности ''O''(t, ·n<sup>2</sup>, ·m) тогда как для точных методов зависимость экспоненциальная. | ||
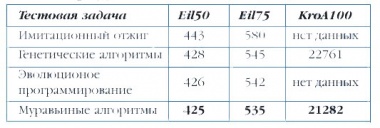
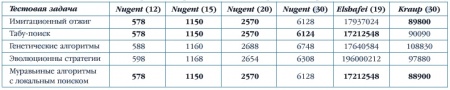
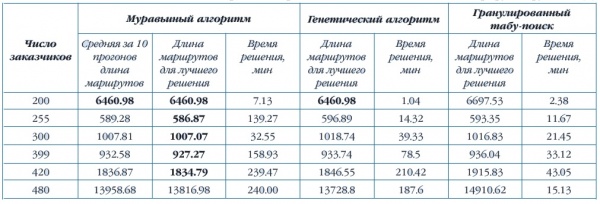
| + | В табл. 1 приведены длины маршрутов коммивояжера, найденные различными эвристическими методами оптимизации. В табл. 2 сравниваются методы решения квадратичной задачи о назначениях. В ячейках таблицы указаны стоимости решений. В табл. 1 и 2 число в названии тестовой задачи указывает ее размерность. В табл. 3 сравниваются три метода оптимизации маршрутов грузовиков для задач большой размерности. Время решения задач пересчитано для компьютера с процессором Pentiumm - 900MHz. Во всех таблицах | ||
| + | полужирным шрифтом выделены наилучшие на сегодняшний день решения. | ||
| + | |||
| + | [[Изображение:Tabl1.jpg|thumb|center|380px|табл.1 Задача коммивояжера]] | ||
| + | |||
| + | [[Изображение:Tabl2.jpg|thumb|center|450px|табл.2 Квадратичная задача о назначениях]] | ||
| + | |||
| + | [[Изображение:Tabl3.jpg|thumb|center|600px|табл.3 Оптимизация маршрута грузовиков]] | ||
| + | |||
| + | =Литература= | ||
| + | # А.А.Ежов, С.А.Шумский Нейрокомпьютинг и его применения в экономике и бизнесе | ||
| + | # Штовба С.Д. Муравьиные алгоритмы // Exponenta Pro. Математика в приложениях, 2003, №4, с.70-75. | ||
| + | # Barker T. and Von Haartman M. Ant Colony Optimization. | ||
| + | |||
| + | =Ссылки= | ||
| + | *http://kovarik.felk.cvut.cz/ant-algorithms/ | ||
| + | *http://courses.washington.edu/inde510/510/Ant Colony Optimization3.ppt | ||
| + | *http://rain.ifmo.ru/cat/ | ||
| + | *http://www.cosc.brocku.ca/Offerings/3P71/Lectures/ACO.ppt | ||
| + | *http://www.orsoc.org.uk/region/regional/swords/swords.ppt | ||
| + | *http://www.iwr.uniiheidelberg.de/iwr/comopt/soft/TSPLIB95/TSPLIB.html | ||
{{ЗаданиеВыполнено|Platonova.Elena|Dj|12 февраля 2010}} | {{ЗаданиеВыполнено|Platonova.Elena|Dj|12 февраля 2010}} | ||
Версия 21:32, 12 февраля 2010
|
Муравьиные алгоритмы серьезно исследуются европейскими учеными с середины 90-х годов. На сегодня уже получены хорошие результаты муравьиной оптимизации таких сложных комбинаторных задач, как: задачи коммивояжера, задачи оптимизации маршрутов грузовиков, задачи раскраски графа, квадратичной задачи о назначениях, оптимизации сетевых графиков, задачи календарного планирования и других. Особенно эффективны муравьиные алгоритмы при on-line оптимизации процессов в распределенных нестационарных системах, например трафиков в телекоммуникационных сетях.
Постановка задачи коммивояжера
В классической постановке, коммивояжер должен объехать N городов по замкнутому маршруту, посетив каждый из них лишь однажды, таким образом, чтобы полная длина его маршрута была минимальной. Если решать задачу коммивояжера „в лоб“ - перебором всех замкнутых путей, связывающих города, то придется проверить все (N-1)!/2 возможных маршрутов, то есть простой метод перебора всех вариантов чрезвычайно неэффективный при большом N. Эффективными же признаются решения, гарантирующие получение ответа за полиномиальное время, растущее как полином с ростом размерности задачи, т.е. как Na. С помощью муравьиных алгоритмов находятся субоптимальные решения, локальные минимумы целевой функции, приближающиеся к абсолютному минимуму.
Принцип работы алгоритма
Муравьиные алгоритмы представляют собой вероятностную жадную эвристику, где вероятности устанавливаются, исходя из информации о качестве решения, полученной из предыдущих решений.
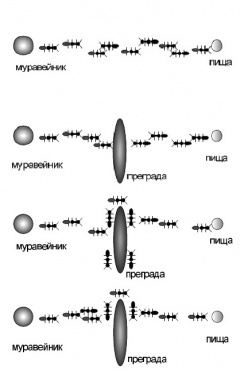
Идея муравьиного алгоритма - моделирование поведения муравьёв, связанного с их способностью быстро находить кратчайший путь от муравейника к источнику пищи и адаптироваться к изменяющимся условиям, находя новый кратчайший путь. При своём движении муравей метит путь феромоном, и эта информация используется другими муравьями для выбора пути. Это элементарное правило поведения и определяет способность муравьёв находить новый путь, если старый оказывается недоступным.
Рассмотрим случай, показанный на рисунке, когда на оптимальном доселе пути возникает преграда. В этом случае необходимо определение нового оптимального пути. Дойдя до преграды, муравьи с равной вероятностью будут обходить её справа и слева. То же самое будет происходить и на обратной стороне преграды. Однако, те муравьи, которые случайно выберут кратчайший путь, будут быстрее его проходить, и за несколько передвижений он будет более обогащён феромоном. Поскольку движение муравьёв определяется концентрацией феромона, то следующие будут предпочитать именно этот путь, продолжая обогащать его феромоном до тех пор, пока этот путь по какой-либо причине не станет недоступен.
Очевидная положительная обратная связь быстро приведёт к тому, что кратчайший путь станет единственным маршрутом движения большинства муравьёв. Моделирование испарения феромона - отрицательной обратной связи - гарантирует нам, что найденное локально оптимальное решение не будет единственным - муравьи будут искать и другие пути. Если мы моделируем процесс такого поведения на некотором графе, рёбра которого представляют собой возможные пути перемещения муравьёв, в течение определённого времени, то наиболее обогащённый феромоном путь по рёбрам этого графа и будет являться решением задачи, полученным с помощью муравьиного алгоритма.
Основные алгоритмические шаги
Любой муравьиный алгоритм, независимо от модификаций, представим в следующем виде
- Пока (условия выхода не выполнены)
- Создаём муравьёв
- Ищем решения
- Обновляем феромон
- Дополнительные действия (опционально)
Теперь рассмотрим каждый шаг в цикле более подробно
- Создаём муравьёв
- Стартовая точка, куда помещается муравей, зависит от ограничений, накладываемых условиями задачи. Потому что для каждой задачи способ размещение муравьёв является определяющим. Либо все они помещаются в одну точку, либо в разные с повторениями, либо без повторений.
- На этом же этапе задаётся начальный уровень феромона. Он инициализируется небольшим положительным числом для того, чтобы на начальном шаге вероятности перехода в следующую вершину не были нулевыми.
- Ищем решения
- Вероятность перехода из вершины i в вершину j определяется по следующей формуле
,
- Вероятность перехода из вершины i в вершину j определяется по следующей формуле
- Обновляем феромон
- Уровень феромона обновляется в соответствии с приведённой формулой
,
- Уровень феромона обновляется в соответствии с приведённой формулой
- Дополнительные действия
- Обычно здесь используется алгоритм локального поиска, однако он может также появиться и после поиска всех решений.
Результаты экспериментов
По сравнению с точными методами, например динамическим программированием или методом ветвей и границ, муравьиный алгоритм находит близкие к оптимуму решения за значительно меньшее время даже для задач большой размерности (n > 20) Время оптимизации муравьиным алгоритмом является полиномиальной функцией от размерности O(t, ·n2, ·m) тогда как для точных методов зависимость экспоненциальная. В табл. 1 приведены длины маршрутов коммивояжера, найденные различными эвристическими методами оптимизации. В табл. 2 сравниваются методы решения квадратичной задачи о назначениях. В ячейках таблицы указаны стоимости решений. В табл. 1 и 2 число в названии тестовой задачи указывает ее размерность. В табл. 3 сравниваются три метода оптимизации маршрутов грузовиков для задач большой размерности. Время решения задач пересчитано для компьютера с процессором Pentiumm - 900MHz. Во всех таблицах полужирным шрифтом выделены наилучшие на сегодняшний день решения.
Литература
- А.А.Ежов, С.А.Шумский Нейрокомпьютинг и его применения в экономике и бизнесе
- Штовба С.Д. Муравьиные алгоритмы // Exponenta Pro. Математика в приложениях, 2003, №4, с.70-75.
- Barker T. and Von Haartman M. Ant Colony Optimization.
Ссылки
- http://kovarik.felk.cvut.cz/ant-algorithms/
- http://courses.washington.edu/inde510/510/Ant Colony Optimization3.ppt
- http://rain.ifmo.ru/cat/
- http://www.cosc.brocku.ca/Offerings/3P71/Lectures/ACO.ppt
- http://www.orsoc.org.uk/region/regional/swords/swords.ppt
- http://www.iwr.uniiheidelberg.de/iwr/comopt/soft/TSPLIB95/TSPLIB.html
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |