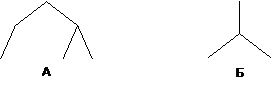Порождение нелинейных регрессионных моделей (пример)
Материал из MachineLearning.
(Новая: '''Порождение нелинейных регрессионных моделей''' - порождение функций, зависящих от параметров и от од...) |
|||
| Строка 7: | Строка 7: | ||
== Дополнительные предположения == | == Дополнительные предположения == | ||
Предполагается, что функции <tex>g^{_{(2)}}_i(w_i,x, y)</tex> корректно работают в случае вызова в виде <tex>g^{_{(2)}}_i(w_i,x)</tex>. | Предполагается, что функции <tex>g^{_{(2)}}_i(w_i,x, y)</tex> корректно работают в случае вызова в виде <tex>g^{_{(2)}}_i(w_i,x)</tex>. | ||
| + | |||
| + | == Интерпретация на языке графов == | ||
| + | Заметим вначале, что суперпозиция функций <tex>G_i</tex> может быть задана двоичным деревом <tex>T(V,X)</tex>, вершины которого <tex>V_i</tex>∈<tex>G_i</tex>, корень – самая внешняя функция суперпозиции. Под глубиной вершины будем понимать расстояние от неё до корня. Если у вершины один потомок, то соответствующая функция запишется как <tex>g_i(g_j)</tex>, если два – то <tex>g_i(g_j,g_k)</tex>, если ноль – то <tex>g_i(x)</tex> или <tex>g_i(x,x)</tex>. | ||
| + | |||
| + | [[Изображение:Clip_image001.gif|300px]] | ||
| + | |||
| + | Так, дереву '''А''' соответствует суперпозиция <tex>2(1(1),2(1,1))</tex>, а дереву '''Б''' – суперпозиция <tex>1(2(1,1))</tex>.<br /> <br /> | ||
| + | Возможна и другая постановка алгоритма. Она особенно ценна, если нельзя вызвать <tex>g^{_{(2)}}_i(x,x)</tex> в виде <tex>g^{_{(2)}}_i(x)</tex>. Изменение состоит в том, что листья дерева суперпозиции считаются не функциями, а свободными переменными. В этом случае дереву '''А''' будет соответствовать суперпозиция <tex>2(1(x), 2(x,x))</tex> дереву '''Б''' – суперпозиция <tex>1(2(x,x))</tex>. | ||
Версия 16:21, 20 апреля 2010
Порождение нелинейных регрессионных моделей - порождение функций, зависящих от параметров и от одной или нескольких свободных переменных. Зависимость от параметров предполагается нелинейной.
Постановка задачи
Задана выборка из пар
. Задан набор порождающих функций одного и двух аргументов
, которые зависят от параметров
и свободных переменных
. Функции гладкие параметрические. Требуется создать алгоритм, порождающий лексикографически упорядоченные суперпозиции возрастающей сложности. Каждая суперпозиция является регрессионной моделью одной независимой переменной. Сравнить качество моделей и регрессионные остатки на порожденном множестве.
Дополнительные предположения
Предполагается, что функции корректно работают в случае вызова в виде
.
Интерпретация на языке графов
Заметим вначале, что суперпозиция функций может быть задана двоичным деревом
, вершины которого
∈
, корень – самая внешняя функция суперпозиции. Под глубиной вершины будем понимать расстояние от неё до корня. Если у вершины один потомок, то соответствующая функция запишется как
, если два – то
, если ноль – то
или
.
Так, дереву А соответствует суперпозиция , а дереву Б – суперпозиция
.
Возможна и другая постановка алгоритма. Она особенно ценна, если нельзя вызвать в виде
. Изменение состоит в том, что листья дерева суперпозиции считаются не функциями, а свободными переменными. В этом случае дереву А будет соответствовать суперпозиция
дереву Б – суперпозиция
.