Нормализация ДНК-микрочипов
Материал из MachineLearning.
м (→Квантильная нормализация) |
м (→Схема выполнения нелинейной нормализации) |
||
| Строка 28: | Строка 28: | ||
Выбрать столбец <tex>j</tex> матрицы <tex>X</tex> в качестве базового. | Выбрать столбец <tex>j</tex> матрицы <tex>X</tex> в качестве базового. | ||
Для всех столбцов <tex>i\neq\j</tex> матрицы настроить параметры нелинейной функции <tex>f</tex>, отображающей столбец <tex>i</tex> на столбец <tex>j</tex>. Пусть <tex>\hat{f}_i</tex> - полученное отображение. | Для всех столбцов <tex>i\neq\j</tex> матрицы настроить параметры нелинейной функции <tex>f</tex>, отображающей столбец <tex>i</tex> на столбец <tex>j</tex>. Пусть <tex>\hat{f}_i</tex> - полученное отображение. | ||
| - | Нормализованные значения в столбце <tex>j</tex> определяются как <tex>\hat{f}_i\left(X_j\right)</tex> | + | Нормализованные значения в столбце <tex>j</tex> определяются как <tex>\hat{f}_i\left(X_j\right).</tex> |
[[Изображение:Quantile-quantile normalization.png|thumb|300px|Метод квантильной нормализации преобразует распределения интенсивностей]] | [[Изображение:Quantile-quantile normalization.png|thumb|300px|Метод квантильной нормализации преобразует распределения интенсивностей]] | ||
| + | |||
=== Квантильная нормализация === | === Квантильная нормализация === | ||
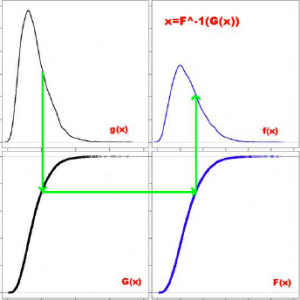
Цель квантильной нормализации - сделать одинаковыми эмпирические распределения интенсивностей всех микрочипов. Для этого используется преобразование вида <tex>x'_i=F^(-1)\left[G\left(x_i\right)\right],</tex> где <tex>G</tex> - эмпирическое распределение интенсивностей каждого чипа, <tex>F</tex> - эмпирическое распределение интенсивностей усреднённого чипа. Можно модифицировать метод, оценивая <tex>F^(-1)</tex> и <tex>G</tex> более гладкими функциями. Однако, для данных большой размерности на практике достаточно и грубой оценки. | Цель квантильной нормализации - сделать одинаковыми эмпирические распределения интенсивностей всех микрочипов. Для этого используется преобразование вида <tex>x'_i=F^(-1)\left[G\left(x_i\right)\right],</tex> где <tex>G</tex> - эмпирическое распределение интенсивностей каждого чипа, <tex>F</tex> - эмпирическое распределение интенсивностей усреднённого чипа. Можно модифицировать метод, оценивая <tex>F^(-1)</tex> и <tex>G</tex> более гладкими функциями. Однако, для данных большой размерности на практике достаточно и грубой оценки. | ||
Версия 05:56, 8 мая 2010
Нормализация - важный этап предобработки ДНК-микрочипов, позволяющий сделать несколько рассматриваемых в эксперименте чипов пригодными к сравнению между собой. Основная цель анализа на этом этапе - исключить влияние систематических небиологических различий между микрочипами. Источников таких различий множество: вариации эффективности обратной транскрипции, маркировки красителями, гибридизации, физические различия между чипами (повреждения, царапины), небольшие различия в концентрации реагентов, вариация лабораторных условий.
Содержание |
Парадигмы нормализации
Нормализация на все гены, нормализация на гены домашнего хозяйства, нормализация на стабильные гены[1]
Методы нормализации
Масштабирование
Один из ДНК-микрочипов выбирается в качестве базового, затем все остальные масштабируются таким образом, чтобы их средняя интенсивность равнялась средней интенсивности базового (этот способ эквивалентен построению линейной регрессии каждого чипа на базовый и последующей нормализации при помощи регрессионной функции).
Для большей устойчивости можно использовать усечённое среднее. Так, в стандартном программном обеспечении производителя микрочипов Affymetrix перед подсчётом среднего отбрасываются по 2% наибольших и наименьших значений интенсивности. Другая модификация — масштабирование к средней интенсивности не по всему базовому чипу, а по каждому подмножеству его проб, соответствующих одному гену.
Affymetrix предлагает использовать масштабирование на последнем этапе предобработки, применяя его непосредственно к матрицам экспрессии, однако, возможно и применение к матрицам интенсивности.
Схема выполнения масштабирования
Выбрать столбецматрицы
в качестве базового. Вычислить (усечённое) среднее
по столбцу
Для всех остальных столбцов матрицы
: вычислить (усечённое) среднее
по столбцу
; вычислить
; каждый элемент столбца
умножить на
.
Нелинейные методы
Предложено большое количество нелинейных способов нормализации данных, использующих различные настраиваемые функции, заменяющие линейную регрессию из предыдущего примера. Среди таких функций cross-validated splines[1], running median lines[1], loess smoothers[1], и т.д. В типичном случае нелинейная нормализация проводится по множеству рангово-инвариантных проб, то есть, проб, имеющих один и тот же ранг во всех микрочипах.
Схема выполнения нелинейной нормализации
Выбрать столбецматрицы
в качестве базового. Для всех столбцов
матрицы настроить параметры нелинейной функции
, отображающей столбец
на столбец
. Пусть
- полученное отображение. Нормализованные значения в столбце
определяются как
.)
Квантильная нормализация
Цель квантильной нормализации - сделать одинаковыми эмпирические распределения интенсивностей всех микрочипов. Для этого используется преобразование вида где
- эмпирическое распределение интенсивностей каждого чипа,
- эмпирическое распределение интенсивностей усреднённого чипа. Можно модифицировать метод, оценивая
и
более гладкими функциями. Однако, для данных большой размерности на практике достаточно и грубой оценки.
Схема выполнения квантильной нормализации
Имеямикрочипов размерности
, построить матрицу
размерности
, где в каждом столбце находятся значения интенсивности по каждому чипу. Отсортировать все столбцы
независимо друг от друга, сформировав матрицу
. Взять среднее по каждой строке матрицы
и создать
- матрицу той же размерности, что и
, в каждой строке которой все значения равны среднему по строке
. Получить матрицу
, переставив значения в столбцах
в том порядке, в каком они стояли в исходной матрице
.
Описанный метод квантильной нормализации - не единственный способ нормализации, основанный на квантилях.