Взвешенное среднее Тьюки
Материал из MachineLearning.
(Новая: Один шаг вычисления взвешенного среднего Тьюки Взвешенное среднее Тьюки ...) |
(/* Одношаговый метод вычисления оценки1. Affymetrix. Statistical Algorithms Description Document, Appendix I. Technical report, Affymetrix. 2002. http://www.affymetrix.com/support/technical/whitepapers/sadd_whitepaper.) |
||
| Строка 5: | Строка 5: | ||
Часто используют только одну итерацию вычисления оценки. | Часто используют только одну итерацию вычисления оценки. | ||
== Одношаговый метод вычисления оценки<ref name="affy2002">1. Affymetrix. Statistical Algorithms Description Document, Appendix I. Technical report, Affymetrix. 2002. http://www.affymetrix.com/support/technical/whitepapers/sadd_whitepaper.pdf</ref>== | == Одношаговый метод вычисления оценки<ref name="affy2002">1. Affymetrix. Statistical Algorithms Description Document, Appendix I. Technical report, Affymetrix. 2002. http://www.affymetrix.com/support/technical/whitepapers/sadd_whitepaper.pdf</ref>== | ||
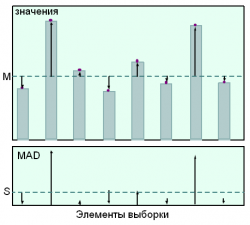
| - | Пусть имеется [[выборка]] <tex>x=\left\{x_1,\ldots,x_n\right\}.</tex> По ней рассчитывается [[ | + | Пусть имеется [[выборка]] <tex>x=\left\{x_1,\ldots,x_n\right\}.</tex> По ней рассчитывается [[медиана]] <tex>M</tex>, затем для каждого наблюдения - модуль его отклонения от медианы. Величина <tex>S</tex> - медиана выборки <tex>\left\{\left|x_1-M\right|,\ldots,\left|x_n-M\right|\right\}</tex> - называется абсолютным отклонением среднего (англ. [http://en.wikipedia.org/wiki/Median_absolute_deviation Median Absolute Deviation, MAD]) и является мерой вариации выборки. |
Для каждого элемента выборки <tex>x_i</tex> вычисляется отклонение от среднего: <tex>u_i=\frac{x_i-M}{cS+\eps}, \:\: i=1,\ldots,n,</tex> где <tex>c</tex> - параметр, от которого зависит чувствительность к отклонениям от среднего, <tex>\eps</tex> - малая постоянная величина, назначение которой - исключить возможность деления на ноль. | Для каждого элемента выборки <tex>x_i</tex> вычисляется отклонение от среднего: <tex>u_i=\frac{x_i-M}{cS+\eps}, \:\: i=1,\ldots,n,</tex> где <tex>c</tex> - параметр, от которого зависит чувствительность к отклонениям от среднего, <tex>\eps</tex> - малая постоянная величина, назначение которой - исключить возможность деления на ноль. | ||
| Строка 14: | Строка 14: | ||
Дополнительное преимущество алгоритма - возможность рассчитать [[доверительный интервал]] для оценки при помощи приближения распределением Стьюдента. Симметричный <tex>(1-\alpha)</tex>% доверительный интервал даётся формулой <br/><tex>T_{bi}\pm t_{df}^{(1-\alpha/2)} \cdot\frac{S_{bi}}{\sqrt{n}},\:\:\: S_{bi} = \sqrt{n}\cdot \frac {\sqrt{ \sum_{\left|u_i\right|\leq 1} \left(x_i-T_{bi}\right)^2 \left(1-u^2 \right)^4 } } { \left| \sum_{\left|u_i\right|\leq 1} \left(1-u_i^2\right) \left(1-5u_i^2\right) \right| },</tex> <br/> где <tex>t_{df}^{(1-\alpha/2)}</tex> - <tex>\left(1-\alpha/2\right)</tex>-квантиль распределения Стьюдента с числом степеней свободы <tex>df=\max\left(0.7*(n-1),1\right).</tex> | Дополнительное преимущество алгоритма - возможность рассчитать [[доверительный интервал]] для оценки при помощи приближения распределением Стьюдента. Симметричный <tex>(1-\alpha)</tex>% доверительный интервал даётся формулой <br/><tex>T_{bi}\pm t_{df}^{(1-\alpha/2)} \cdot\frac{S_{bi}}{\sqrt{n}},\:\:\: S_{bi} = \sqrt{n}\cdot \frac {\sqrt{ \sum_{\left|u_i\right|\leq 1} \left(x_i-T_{bi}\right)^2 \left(1-u^2 \right)^4 } } { \left| \sum_{\left|u_i\right|\leq 1} \left(1-u_i^2\right) \left(1-5u_i^2\right) \right| },</tex> <br/> где <tex>t_{df}^{(1-\alpha/2)}</tex> - <tex>\left(1-\alpha/2\right)</tex>-квантиль распределения Стьюдента с числом степеней свободы <tex>df=\max\left(0.7*(n-1),1\right).</tex> | ||
| + | |||
== Итерационный метод вычисления оценки== | == Итерационный метод вычисления оценки== | ||
== Литература == | == Литература == | ||
Версия 09:42, 13 мая 2010
Взвешенное среднее Тьюки - оценка среднего значения выборки, устойчивая к наличию выбросов. Алгоритм вычисления оценки носит итерационный характер. До достижения сходимости повторяются следующие шаги:
- Вычисляется оценка среднего значения выборки (в начала работы алгоритма - обычная медиана).
- Определяются расстояния от вычисленного среднего до каждого элемента выборки. Согласно этим расстояниям, элементам выборки присваиваются различные веса, с учётом которых среднее значение пересчитывается. Характер весовой функции таков, что наблюдения, отстоящие от среднего достаточно далеко, не вносят большого вклада в значение взвешенного среднего.
Часто используют только одну итерацию вычисления оценки.
Содержание |
Одношаговый метод вычисления оценки[1]
Пусть имеется выборка По ней рассчитывается медиана
, затем для каждого наблюдения - модуль его отклонения от медианы. Величина
- медиана выборки
- называется абсолютным отклонением среднего (англ. Median Absolute Deviation, MAD) и является мерой вариации выборки.
Для каждого элемента выборки вычисляется отклонение от среднего:
где
- параметр, от которого зависит чувствительность к отклонениям от среднего,
- малая постоянная величина, назначение которой - исключить возможность деления на ноль.
Для взвешивания используется биквадратичная функция:
Итоговое значение среднего вычисляется по следующей формуле:
Дополнительное преимущество алгоритма - возможность рассчитать доверительный интервал для оценки при помощи приближения распределением Стьюдента. Симметричный % доверительный интервал даётся формулой
где -
-квантиль распределения Стьюдента с числом степеней свободы
Итерационный метод вычисления оценки
Литература
Hoaglin, D.C., Mosteller, F., Tukey, J.W. Understanding Robust and Exploratory Data Analysis. John Wiley & Sons, New York (2000).