Распределение Пуассона

Материал из MachineLearning.

(Различия между версиями)

Riabenko (Обсуждение | вклад)
(Новая: {{Вероятностное распределение| name =Распределение Пуассона| type =Функция| pdf_image =[[Изображение:P...)
К следующему изменению →

Версия 13:27, 8 ноября 2010

**Распределение Пуассона**
Функция вероятности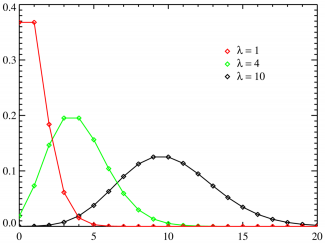
Функция распределения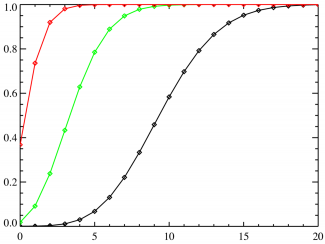
Параметры	$\lambda \in (0,\infty)$
Носитель	$k \in \{0,1,2,\ldots\}$
Функция вероятности	$\frac{e^{-\lambda} \lambda^k}{k!}\!$
Функция распределения	$\frac{\Gamma(k+1, \lambda)}{k!}\!$
Математическое ожидание	$\lambda\,$
Медиана	N/A
Мода	$\lfloor\lambda\rfloor$
Дисперсия	$\lambda\,$
Коэффициент асимметрии	$\lambda^{-1/2}\,$
Коэффициент эксцесса	$\lambda^{-1}\,$
Информационная энтропия	$\lambda[1\!-\!\ln(\lambda)]\!+\!e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\ln(k!)}{k!}$
Производящая функция моментов	$\exp(\lambda (e^t-1))\,$
Характеристическая функция	$\exp(\lambda (e^{it}-1))\,$

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Определение

Выберем фиксированное число $\lambda > 0$ и определим дискретное распределение, задаваемое следующей функцией вероятности:

$p(k) \equiv \mathbb{P}(Y=k) = \frac{\lambda^k}{k!}\, e^{-\lambda}$ ,

где

$k!$ обозначает факториал,
$e = 2.718281828\ldots$ — основание натурального логарифма.

Тот факт, что случайная величина $Y$ имеет распределение Пуассона с параметром $\lambda$ , записывается: $Y \sim~ \mathrm{P}(\lambda)$ .

Моменты

Производящая функция моментов распределения Пуассона имеет вид:

$E_Y(t)=e^{\lambda\left(e^t-1\right)}$ ,

откуда

$\mathbb{M}[Y]=\lambda$ ,

$\mathbb{D}[Y]=\lambda$ .

Для факториальных моментов распределения справедлива общая формула:

$\mathbb{M}Y^{[k]}=\lambda^k$ ,

где $k=1,2,...$

А так как моменты и факториальные моменты линейным образом связаны, то часто для Пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.

Свойства распределения Пуассона

Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть $Y_i\sim\mathrm{P}(\lambda_i),\; i=1,\ldots,n$ . Тогда

$Y = \sum\limits_{i=1}^n Y_i \sim \mathrm{P}\left(\sum\limits_{i=1}^n \lambda_i\right)$ .

Пусть $Y_i \sim \mathrm{P}(\lambda_i),\; i=1,2$ , и $Y = Y_1 + Y_2$ . Тогда условное распределение $Y_1$ при условии, что $Y = y$ , биномиально. Более точно: