Участник:Anton/Песочница
Материал из MachineLearning.
| Строка 1: | Строка 1: | ||
| - | + | __NOTOC__ | |
| - | + | [[Байесовские методы машинного обучения (курс лекций, Д.П. Ветров, Д.А. Кропотов)|Перейти к основной странице спецкурса]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | '''Начало выполнения задания''': 22 ноября 2010 г.<br> | |
| - | + | '''Срок сдачи''': {{важно|6 декабря 2010 г., 23:59.}} | |
| - | + | ||
| - | + | ||
| - | < | + | |
| - | ''' | + | ==Модель Изинга== |
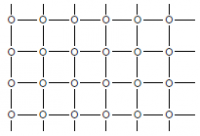
| + | [[Изображение:BayesML2010_task2_rectGrid.PNG|200px|thumb|Прямоугольная система соседства]] | ||
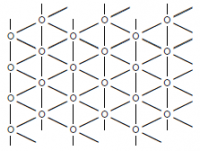
| + | [[Изображение:BayesML2010_task2_triGrid.PNG|200px|thumb|Треугольная система соседства]] | ||
| + | '''Модель Изинга''' — математическая модель статистической физики, предназначенная для описания намагничивания материала. | ||
| + | Каждой вершине кристаллической решётки (рассматриваются не только трёхмерные, но и одно- и двумерные случаи) сопоставляется число, называемое спином и равное +1 или −1 («поле вверх»/«поле вниз»). Каждому из <tex>2^N</tex> возможных вариантов расположения спинов (где N — число атомов решётки) приписывается энергия, получающаяся из попарного взаимодействия спинов соседних атомов J и действия внешнего магнитного поля H:<br> | ||
| + | <tex> | ||
| + | E(X) = -\left( \sum_{(i,j) \in E} J_{ij}x_i x_j + \sum_{i=1}^N H_i x_i \right), | ||
| + | </tex><br> | ||
| + | где <tex>x_i</tex> - переменные, соответствующие спинам, E - система соседства (в данном задании рассматривается 2 системы соседства: прямоугольная и треугольная) . Вероятность нахождения в каждом конкретном состоянии задается распределением Гиббса:<br> | ||
| + | <tex> | ||
| + | P(X) = \frac{1}{Z} \exp{\left( -\beta E(X) \right)}, \qquad \beta = \frac{1}{kT}, | ||
| + | </tex><br> | ||
| + | где Z - нормировочная константа, T - температура, k - параметр. | ||
| - | + | Если <tex>J_{ij} = 1 </tex>,то вещество называется ферромагнетиком. Если <tex>J_{ij} = -1</tex>, то вещество называется антиферромагнетиком. | |
| - | + | ==Вариант 1== | |
| - | + | ===Описание задания=== | |
| + | Провести исследование модели Изинга методом Монте-Карло. В качестве алгоритма генерации выборки использовать метод Гиббса. | ||
| + | Генерацию каждого элемента решетки проводить по следующим формулам: | ||
| + | <br><tex> | ||
| + | p(x_i = 1 | X_{/\{i\}}) = \frac{1}{1 + \exp(-2\beta b_i)}, \qquad b_i = \sum_{j: (i, j) \in E} J_{ij}x_j + H_i, | ||
| + | </tex><br> | ||
| + | <tex> | ||
| + | p(x_i = -1 | X_{/\{i\}}) = \frac{\exp(-2\beta b_i)}{1 + \exp(-2\beta b_i)}. | ||
| + | </tex> | ||
| - | [[ | + | ===Задание=== |
| - | + | [[Изображение:BayesML2010_task2_example.PNG|200px|thumb|Пример иллюстрации состояния модели Изинга размера 20 на 20.]] | |
| - | + | # Вывести формулы для метода Гиббса генерации выборки методом Гиббса (вывод вставить в отчет). | |
| - | * | + | # Реализовать процедуру подсчета математического ожидания и дисперсии энергии (нормированной на количество спинов N), математического ожидания квадрата общей намагниченности модели <tex>\mu = \left(\sum_{i=1}^N x_i \right) / N</tex> методов Гиббса (с заданным числом итераций) для заданных параметров <tex>\beta</tex> и заданного внешнего магнитного поля H. (Требования по эффективности реализации: 1000 итераций метода Гиббса для решетки размером 20 на 20 и 100 значений параметра <tex>\beta</tex> должны выполнятся не более 100 секунд.) |
| - | * | + | # Построить графики зависимости <tex>\mathbb{E}E, \sqrt{\mathbb{D}E}, \sqrt{\mathbb{E}(\mu^2)}</tex> от температуры для треугольной и четырехугольной систем соседства, ферромагнетика и антиферромагнетика (всего 4 модели). Проинтерпретировать полученные результаты (в частности идентифицировать, локализовать и изучить фазовый переход). Для построения графиков использовать следующие значения параметров: |
| - | * | + | #*размер решетки 20 на 20 (N = 400) |
| - | + | #*<tex>k = 1</tex> | |
| - | + | #*10000 итераций метода Гиббса для каждой из температур | |
| + | #*для ферромагнетика <tex>J_{ij} = 1</tex>, для антиферромагнетика <tex>J_{ij} = -1</tex> | ||
| + | #*внешнее магнитное поле <tex>H_i = 0</tex> | ||
| + | #*температуры T = 0.5 : 0.1 : 10; | ||
| + | #Для ферромагнетика с четырехугольной системой связности привести (картинками) характерные состояния для разных температур в окрестности фазового перехода. Проинтерпретировать результаты. Рассмотреть не менее одного примера для не менее 5 разных температур. Параметры генерации те же, что и в пункте 3. | ||
| + | #Исследовать влияние фазового перехода в ферромагнетике с прямоугольной системой соседства от равномерного внешнего магнитного поля. Параметры модели взять такие же как в пункте 3. | ||
| + | #Выполнить пункт 4 в присутствии внешнего магнитного поля следующей структуры: на половине решетки H = 1, на другой половине H = -1. | ||
| + | #Сравнить результаты применения метода Монте-Карло с результатами применения вариационного подхода. Рассмотреть ферромагнетик с прямоугольной системой соседства. Реализацию вариационного подхода взять у товарища, выполняющего вариант 2. Привести графики математического ожидания и дисперсии энергии, корня из математического ожидания намагниченности в одних осях для двух подходов. | ||
| + | === Оформление задания === | ||
| - | + | Выполненное задание следует отправить письмом по адресу ''bayesml@gmail.com'' с заголовком письма «Задание 2 <Номер_группы> <ФИО>». Убедительная просьба присылать выполненное задание '''только один раз''' с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | В качестве программной среды реализации настоятельно рекомендуется использовать MATLAB. Тем не менее, никаких ограничений на выбор среды реализации не накладывается. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Присланный вариант задания должен содержать в себе: | |
| - | * | + | * ФИО исполнителя, номер группы и номер варианта задания. |
| - | * | + | * Текстовый файл в формате PDF, содержащий описание проведенных исследований. |
| - | * | + | * Все исходные коды с необходимыми комментариями. |
| - | * | + | * Дополнительные комментарии или материалы, если необходимо. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | [ | + | Исходные коды должны включать в себя реализацию метода Гиббса для прямоугольной и треугольной систем соседств в виде отдельных функций. Прототипы функций имеют следующий вид:<br> |
| - | + | {|class="standard" | |
| + | !''Метод Гиббса'' | ||
| + | |- | ||
| + | |[E, magnet, samples] = generateIsing4(vS, hS, J, H, iter, betaAll) - прямоугольная система соседства | ||
| + | |- | ||
| + | |[E, magnet, samples] = generateIsing6(vS, hS, J, H, iter, betaAll) - треугольная система соседства | ||
| + | |- | ||
| + | |ВХОД | ||
| + | |- | ||
| + | | | ||
| + | {|border="0" | ||
| + | |vS — размер решетки по вертикали; | ||
| + | |- | ||
| + | |hS — размер решетки по горизонтали; | ||
| + | |- | ||
| + | |J - параметр J модели. Все <tex>J_{ij}</tex> одинаковы и равны J. | ||
| + | |- | ||
| + | |H - внешнее магнитное поле, матрица размера vS на hS. | ||
| + | |- | ||
| + | |iter - количество итераций метода Гиббса | ||
| + | |- | ||
| + | |betaAll - вектор значений параметра <tex>\beta</tex>, для которых надо применить метод Гиббса. Длина вектора - <tex>\beta_0</tex>. | ||
| + | |} | ||
| + | |- | ||
| + | |ВЫХОД | ||
| + | |- | ||
| + | | | ||
| + | {| | ||
| + | |E - значения энергий на 1 спин, массив размера iter на <tex>\beta_0</tex>. | ||
| + | |- | ||
| + | |magnet — значения магнетизации на 1 спин, массив размера iter на <tex>\beta_0</tex>. | ||
| + | |- | ||
| + | |samples — примеры положений модели для всех температур, массив размера vS на hS на <tex>\beta_0</tex>. | ||
| + | |} | ||
| + | |} | ||
| - | == | + | ===Рекомендации=== |
| - | * | + | *Лучше реализовывать метод векторно по параметру <tex>\beta</tex>, то есть проводить вычисления для всех температур сразу. |
| - | * | + | *Начинать метод Гиббса лучше с наиболее вероятной для данной модели конфигурации. |
| - | * | + | *Для оценки глобальных параметров лучше выкинуть значения, полученные на первой трети итераций метода Гиббса. |
| + | *В качестве примера ситуации можно взять ситуацию, сгенерированную на последней итерации метода Гиббса. | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | + | ==Вариант 2== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | = | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | = | + | |
| - | + | ||
| - | + | ||
| - | + | ||
Версия 13:23, 20 ноября 2010
Перейти к основной странице спецкурса
Начало выполнения задания: 22 ноября 2010 г.
Срок сдачи: 6 декабря 2010 г., 23:59.
Модель Изинга
Модель Изинга — математическая модель статистической физики, предназначенная для описания намагничивания материала.
Каждой вершине кристаллической решётки (рассматриваются не только трёхмерные, но и одно- и двумерные случаи) сопоставляется число, называемое спином и равное +1 или −1 («поле вверх»/«поле вниз»). Каждому из возможных вариантов расположения спинов (где N — число атомов решётки) приписывается энергия, получающаяся из попарного взаимодействия спинов соседних атомов J и действия внешнего магнитного поля H:
где - переменные, соответствующие спинам, E - система соседства (в данном задании рассматривается 2 системы соседства: прямоугольная и треугольная) . Вероятность нахождения в каждом конкретном состоянии задается распределением Гиббса:
где Z - нормировочная константа, T - температура, k - параметр.
Если ,то вещество называется ферромагнетиком. Если
, то вещество называется антиферромагнетиком.
Вариант 1
Описание задания
Провести исследование модели Изинга методом Монте-Карло. В качестве алгоритма генерации выборки использовать метод Гиббса.
Генерацию каждого элемента решетки проводить по следующим формулам:
Задание
- Вывести формулы для метода Гиббса генерации выборки методом Гиббса (вывод вставить в отчет).
- Реализовать процедуру подсчета математического ожидания и дисперсии энергии (нормированной на количество спинов N), математического ожидания квадрата общей намагниченности модели
методов Гиббса (с заданным числом итераций) для заданных параметров
и заданного внешнего магнитного поля H. (Требования по эффективности реализации: 1000 итераций метода Гиббса для решетки размером 20 на 20 и 100 значений параметра
должны выполнятся не более 100 секунд.)
- Построить графики зависимости
от температуры для треугольной и четырехугольной систем соседства, ферромагнетика и антиферромагнетика (всего 4 модели). Проинтерпретировать полученные результаты (в частности идентифицировать, локализовать и изучить фазовый переход). Для построения графиков использовать следующие значения параметров:
- размер решетки 20 на 20 (N = 400)
- 10000 итераций метода Гиббса для каждой из температур
- для ферромагнетика
, для антиферромагнетика
- внешнее магнитное поле
- температуры T = 0.5 : 0.1 : 10;
- Для ферромагнетика с четырехугольной системой связности привести (картинками) характерные состояния для разных температур в окрестности фазового перехода. Проинтерпретировать результаты. Рассмотреть не менее одного примера для не менее 5 разных температур. Параметры генерации те же, что и в пункте 3.
- Исследовать влияние фазового перехода в ферромагнетике с прямоугольной системой соседства от равномерного внешнего магнитного поля. Параметры модели взять такие же как в пункте 3.
- Выполнить пункт 4 в присутствии внешнего магнитного поля следующей структуры: на половине решетки H = 1, на другой половине H = -1.
- Сравнить результаты применения метода Монте-Карло с результатами применения вариационного подхода. Рассмотреть ферромагнетик с прямоугольной системой соседства. Реализацию вариационного подхода взять у товарища, выполняющего вариант 2. Привести графики математического ожидания и дисперсии энергии, корня из математического ожидания намагниченности в одних осях для двух подходов.
Оформление задания
Выполненное задание следует отправить письмом по адресу bayesml@gmail.com с заголовком письма «Задание 2 <Номер_группы> <ФИО>». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Новые версии будут рассматриваться только в самом крайнем случае.
В качестве программной среды реализации настоятельно рекомендуется использовать MATLAB. Тем не менее, никаких ограничений на выбор среды реализации не накладывается.
Присланный вариант задания должен содержать в себе:
- ФИО исполнителя, номер группы и номер варианта задания.
- Текстовый файл в формате PDF, содержащий описание проведенных исследований.
- Все исходные коды с необходимыми комментариями.
- Дополнительные комментарии или материалы, если необходимо.
Исходные коды должны включать в себя реализацию метода Гиббса для прямоугольной и треугольной систем соседств в виде отдельных функций. Прототипы функций имеют следующий вид:
| Метод Гиббса | ||||||
|---|---|---|---|---|---|---|
| [E, magnet, samples] = generateIsing4(vS, hS, J, H, iter, betaAll) - прямоугольная система соседства | ||||||
| [E, magnet, samples] = generateIsing6(vS, hS, J, H, iter, betaAll) - треугольная система соседства | ||||||
| ВХОД | ||||||
| ||||||
| ВЫХОД | ||||||
|
Рекомендации
- Лучше реализовывать метод векторно по параметру
, то есть проводить вычисления для всех температур сразу.
- Начинать метод Гиббса лучше с наиболее вероятной для данной модели конфигурации.
- Для оценки глобальных параметров лучше выкинуть значения, полученные на первой трети итераций метода Гиббса.
- В качестве примера ситуации можно взять ситуацию, сгенерированную на последней итерации метода Гиббса.