Аппроксимация Лапласа (пример)

Материал из MachineLearning.

(Различия между версиями)

Версия 00:05, 24 ноября 2010

Аппроксимация Лапласа - способ оценки параметров нахождения нормального распределения при апроксимации заданой плотности вероятности.

Содержание

1 Сэмплирование
2 Постановка задачи
3 Описание алгоритма
4 Вычислительный эксперимент
- 4.1 Пример 1
5 Смотри также
6 Литература
7 Примечания

Сэмплирование

Сэмплирование – метод выбора подмножества наблюдаемых величин из данного множества, с целью выделения неких свойст исходного множества. Одно из основных приминений методов сэмплирования заключается в оценке математического ожидания сложных вероятностных распределений:

$E[f]=\int f(z)p(z) dz$

для которых данный инеграл не может быть подсчитан аналитическим методом (к примеру, ввиду сложного аналитического вида распределения $p(z)$ ). Однако, можно подсчитать значение p(z) в любой точке z. Основная идея заключается в создании незавсимой выборки $z^{(l)}$ (где $l=1,...,L$ ) из распределения $p(z)$ . Это позволит оцениваемое математическое ожидание приблизить конечной суммой:

$\hat f=\frac{1}{L}\sum_{l=1}^{L} f(z^{(l)})$

Существует несколько методов сэмплирования для создания выборки $z^{(l)}$ ^[1]:

Simple random sampling;
Systematic sampling;
Rejection sampling;
Adaptive rejection sampling.

Постановка задачи

Задана выборка — множество $X^N=\{{x}_1,\ldots,{x}_N|x\in\R^M\}$ значений свободных переменных и множество $\{y_1,\ldots, y_N| y\in\R\}$ соответствующих им значений зависимой переменной. Необходимо для выбранной регрессионной модели $f(w,x)$ :

показать зависимость среднеквадратичной ошибки от значений параметров модели: $SSE=SSE(w)$ ;
построить график и сделать апроксимацию Лапласа для нее;
найти расстояния между получеными зависимостями, используя расстояние Кульбака - Лейблера.

Описание алгоритма

При востановлении регрессии рассматривалась следующая гипотеза порождения данных:

$y=f(x,w)$

В таком случае, при фиксированной модели f плотность вероятности появления данных равняется^[1]:

$p(y|x,w)=\frac{1}{Z_D}exp(-E_D)$ , где

$E_D$ - это функция регрессионных невязок, т.е. $SSE$ ;

$Z_D$ - нормировачный коэффициент.

1. В заданной модели f, используя метод наименьших квадратов, находим оптимальное значение вектора параметров $\mathcal w_{opt}$ . Далее, фиксируем все параметры выбранной регрессионной модели (для определенности зададим им оптимальные значения) кроме одного (пусть этот незафиксированный параметр будет w(1)). После чего, варируя значение w(1), строим искомую зависимость $SSE=SSE(w(1))$ и его график. Таким образом построена зависимость от одного параметра w(1). Аналогично действуя, строится зависимость от большего количества параметров.

2. При построении апроксимации Лапласса вначале рассмотрим одномерный случай. Пусть есть распределение p(z):

$p(z)=\frac{1}{Z}f(z)$ , где

$Z=\int f(z)dz$ - нормировочный коэффициент.

Первый шаг при построении апроксимации Лапласса, нахождение максимума, т.е. такого $z_0$ , что $p'(z_0)=0$ . Далее, раскладываем $lnf(z)$ в ряд Тейлора в окресности $z_0$ :

$lnf(z)=lnf(z_0)-\frac{1}{2}A(z-z_0)^2$

где

$A=-\frac{d^2}{dz^2}lnf(z)|_{z=z_0}$ .

Тогда

$f(z)=f(z_0)exp(-\frac{A}{2}(z-z_0)^2)$ .

Апроксимация Лапласса примет вид:

$q(z)=(\frac{A}{2 pi})^{1/2}exp(-\frac{A}{2}(z-z_0)^2)$ .

В многомерном случае (размерности M), аналогично действуя, придем к:

$q(z)=(\frac{|A|}{(2 pi)^M})^{1/2}exp(-\frac{1}{2}(z-z_0)^T A (z-z_0))$ .

где A Гаусиан, размера M x M, равный:

$A=-\nabla \nabla lnf(z)|_{z=z_0}$ .

3. Расстояние Кульбака - Лейблера между двумя распределениями p(z) и q(z) равняется:

$D_{kl}(p,q)=\sum\limits_{x\in \mathcal{X}} p(x) \ln \frac{p(x)}{q(x)}$

Вычислительный эксперимент

Обозначим плоность распределения SSE как $p_{SSE}$ , а его апроксимация лапласса $p_{lap}$ .

Однако, во время вычислительного эксперимента SSE принимало достаточно большие значения (порядка $10^3 - 10^4$ ). Как следствие, p(y|x,w) принимало значения порядка 1, и апроксимация Лапласса была некоректной. Поэтому, апроксимация Лапласса применялась не к самому распределению p(y|x,w), а к ln(p(y|x,w)) (т.е. к -SSE c точностью до коэффициента).

Пример 1

Задуманная функция $y=x + sin3x$ . Берем линейную регрессионную модель с двумя параметрами: $y(x)=w_1+w_2x$ . Используя метод наименьших квадратов находим оптимальное значение $w_1_{opt}$ и $w_2_{opt}$ (при которых SSE минимально).

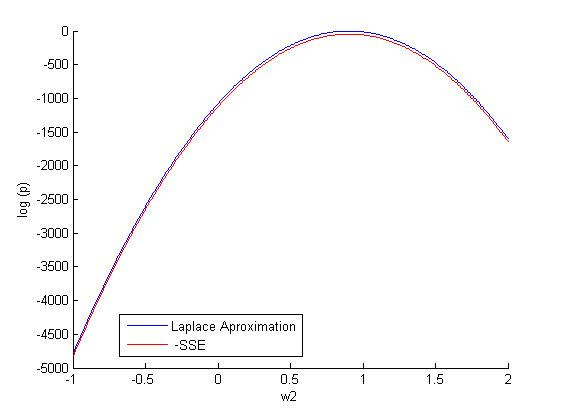
При фиксированном $w_1=w_1_{opt}$ задаем различные значение $w_2$ (500 случайных значений на отрезке [-1;2]) и строим зависимость:

$D_{kl}(p_{SSE},p_{lap})=0.0085$ .

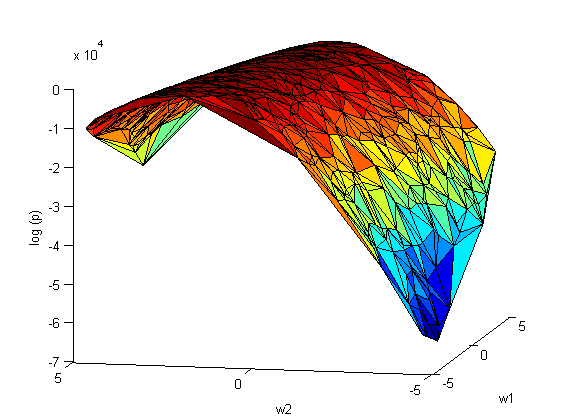
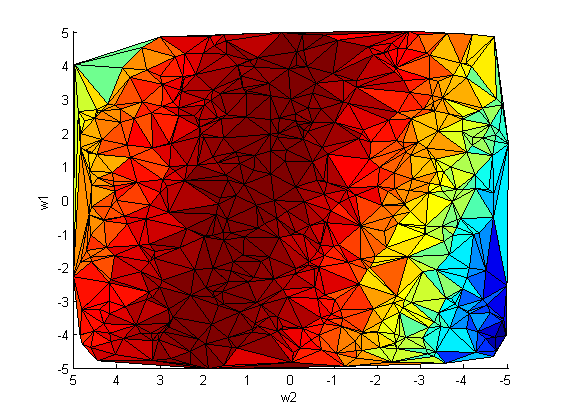
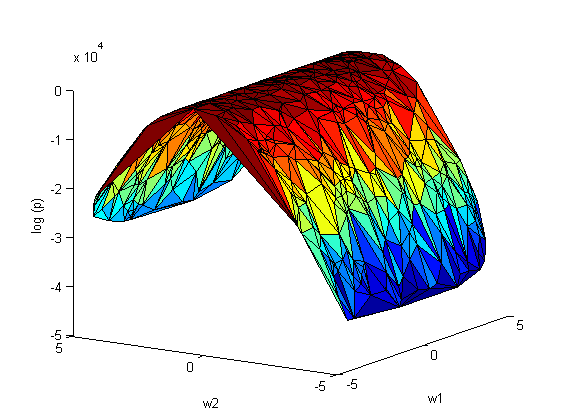
Повторим эксперимент, только теперь варируем сразу оба параметра $w_1$ и $w_2$ :

Рис. 1. Зависимость $- SSE$ от $w_1$ и $w_2$

Рис. 2. Зависимость от и . Ось log(p) направлена вверх

Рис. 2. Зависимость $- SSE$ от $w_1$ и $w_2$ . Ось log(p) направлена вверх

апроксимация Лапласса:

Laplace approximation

$D_{kl}(p_{SSE},p_{lap})=1.2481$

На рис.2 наблюдается зависимость между коэффициентами $w_1$ и $w_2$ . Следовательно, ковариационная матрица $cov(w_1,w_2)$ не будет диагональной.

Смотри также

Литература

Bishop, C. Pattern Recognition And Machine Learning. Springer. 2006.

Примечания

Данная статья является непроверенным учебным заданием.

Студент: Евгений Зайцев

Преподаватель: В.В.Стрижов

Срок: 24 декабря 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%90%D0%BF%D0%BF%D1%80%D0%BE%D0%BA%D1%81%D0%B8%D0%BC%D0%B0%D1%86%D0%B8%D1%8F_%D0%9B%D0%B0%D0%BF%D0%BB%D0%B0%D1%81%D0%B0_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категории: Непроверенные учебные задания | Практика и вычислительные эксперименты

@@ Строка 61: / Строка 61: @@
 <center><tex>A=-\nabla \nabla lnf(z)|_{z=z_0}</tex>.</center>
-'''3'''. Расстояние Кульбака - Лейблера:
+'''3'''. Расстояние Кульбака - Лейблера между двумя распределениями ''p(z)'' и ''q(z)'' равняется:
 <center> <tex>D_{kl}(p,q)=\sum\limits_{x\in \mathcal{X}} p(x) \ln \frac{p(x)}{q(x)}</tex></center>