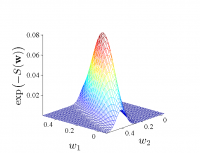
Аппроксимация функции ошибки
Материал из MachineLearning.
| Строка 3: | Строка 3: | ||
== Постановка задачи == | == Постановка задачи == | ||
| - | + | Дана выборка <tex>D = \{(x_i, y_i)\}_{i = 1}^N</tex>, где <tex>x_i \in \mathbb{R}^n, i = 1, \dots, N</tex> - вектора независимой переменной, а <tex>y_i \in \mathbb{R}, i = 1, \dots, N</tex> - значения зависимой переменной. | |
| + | |||
| + | Предполагается, что <tex>y = f(x, w),</tex> | ||
| + | |||
| + | где <tex>f(x, w)</tex> - некоторая параметрическая функция, <tex>w \in W</tex> - вектор ее параметров. Предполагается, что задано апостериорное распределение параметров модели <tex>p(w | D, f)</tex>, которому соответствует функция ошибки <tex>S(w)</tex>: <tex>p(w | D, f) = \frac{exp(-S(w))}{Z_S}</tex>. Пусть <tex>w_{MP} = \arg\max_w p(w | D, f)</tex> - наиболее вероятные параметры модели. Требуется найти аппроксимацию Лапласа для функции <tex>p(w | D, f)</tex> в точке <tex>w_{MP}</tex>. Заметим, что в данной работе в качестве функции ошибки берется сумма квадратов ошибок аппроксимации <tex>S(w) = \sum_{i = 1}^N (y_i - f(x_i, w))^2</tex>. | ||
== Описание решения == | == Описание решения == | ||
Версия 13:38, 26 сентября 2011
|
В работе рассматривается метод аппроксимации функции ошибки функцией многомерного нормального распределения. Рассматриваются случаи матрицы ковариации общего вида, диагональной матрицы ковариации, а также диагональной матрицы ковариации с равными значениями дисперсии. Для нормировки получившихся функций распределения используется аппроксимация Лапласа.
Постановка задачи
Дана выборка , где
- вектора независимой переменной, а
- значения зависимой переменной.
Предполагается, что,)
где- некоторая параметрическая функция,
- вектор ее параметров. Предполагается, что задано апостериорное распределение параметров модели
, которому соответствует функция ошибки
:
. Пусть
- наиболее вероятные параметры модели. Требуется найти аппроксимацию Лапласа для функции
в точке
. Заметим, что в данной работе в качестве функции ошибки берется сумма квадратов ошибок аппроксимации
.
Описание решения
- настолько подробно, что по математическому описанию можно было бы восстановить код
Вычислительный эксперимент
Цель вычислительного эксперимента - ...
- описание эксперимента
- иллюстрации с комментариями
y = 1; % There is no need to post all your code here. Only extracts and only if it is necessary.
Требования к оформлению графиков:
- шрифт должен быть больше,
- толщина линий равна двум,
- заголовки осей с большой буквы,
- заголовок графика отсутствует (чтобы не дублировать подпись в статье);
- рекомендуется сразу сохранять EPS и PNG (для TeX и для Wiki).
h = figure; hold('on'); plot(xi,y,'r-', 'Linewidth', 2); plot(xi,y,'b.', 'MarkerSize', 12); axis('tight'); xlabel('Time, $\xi$', 'FontSize', 24, 'FontName', 'Times', 'Interpreter','latex'); ylabel('Value, $y$', 'FontSize', 24, 'FontName', 'Times', 'Interpreter','latex'); set(gca, 'FontSize', 24, 'FontName', 'Times') saveas(h,'ModelOne.eps', 'psc2'); saveas(h,'ModelOne.png', 'png');
Исходный код и полный текст работы
Смотри также
Литература
| | Данная статья является непроверенным учебным заданием.
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |