М-оценка

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м (Новая: М-оценки — широкий класс статистических оценок, доставляющих минимум суммы каких-либо функций от дан...)
Текущая версия (10:53, 24 октября 2011) (править) (отменить)
м
 
Строка 16: Строка 16:
::<tex>\sum_{i=1}^n \psi\left(x_i-\theta\right)=0.</tex>
::<tex>\sum_{i=1}^n \psi\left(x_i-\theta\right)=0.</tex>
-
<!--Чтобы сделать М-оценку независимой от коэффициента масштаба распределения, можно перейти к задаче
+
Чтобы сделать М-оценку независимой от коэффициента масштаба распределения, можно перейти к задаче
-
::<tex>\min_{\displaystyle\theta}\sum_{i=1}^n\rho\left(\frac{x_i - \theta}{s}\right), \,\!</tex>-->
+
::<tex>\min_{\displaystyle\theta}\sum_{i=1}^n\rho\left(\frac{x_i - \theta}{s}\right), \,\!</tex>
 +
::<tex>\sum_{i=1}^n\psi\left(\frac{x_i - \theta}{s}\right)=0,</tex>
 +
где значение параметра <tex>s</tex> можно находить вместе с <tex>\theta</tex>, а можно считать в данной задаче известным, используя какую-либо оценку (например, [[абсолютное отклонение среднего]]).
 +
 
 +
Иногда от этой задаче переходят к задаче вида
 +
::<tex>\sum_{i=1}^n w\left(r_i\right) r_i = 0, </tex>
 +
где <tex>r_i=\frac{x_i - \theta}{s}</tex>, <tex>w\left(r_i\right)=\frac{\psi\left(r_i\right)}{r_i}</tex> — весовая функция. Оценка параметра тогда получается как решение итерационно перевзвешиваемой задачи наименьших квадратов:
 +
::<tex>\sum_{i=1}^n w\left(r_i^{(k-1)}\right)r_i^{(k)},</tex>
 +
где k — номер итерации.
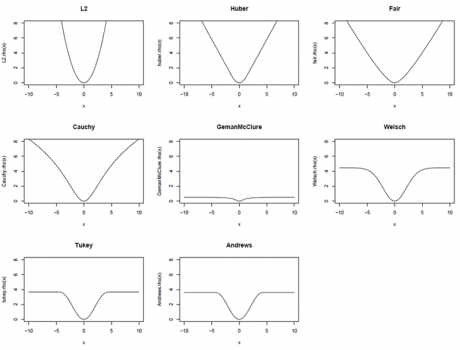
[[Изображение:M-estimator_rho.png‎|thumb|460px|Вид функции <tex>\rho</tex> для некоторых популярных М-оценок.]]
[[Изображение:M-estimator_rho.png‎|thumb|460px|Вид функции <tex>\rho</tex> для некоторых популярных М-оценок.]]
{| class="wikitable"
{| class="wikitable"
Строка 24: Строка 32:
! <tex>\rho(x)</tex>
! <tex>\rho(x)</tex>
! <tex>\psi(x)</tex>
! <tex>\psi(x)</tex>
-
<!-- <tex>w(x)</tex> -->
+
! <tex>w(x)</tex>
|-
|-
! Huber
! Huber
| <tex>\begin{cases}x^2/2, & |x|\leq k \\ k\left(|x|-k/2\right), & |x|>k \end{cases}</tex>
| <tex>\begin{cases}x^2/2, & |x|\leq k \\ k\left(|x|-k/2\right), & |x|>k \end{cases}</tex>
| <tex>\begin{cases}x, & |x|\leq k \\ k\operatorname{sgn}(x), & |x|>k \end{cases}</tex>
| <tex>\begin{cases}x, & |x|\leq k \\ k\operatorname{sgn}(x), & |x|>k \end{cases}</tex>
-
<!-- | <tex>\begin{cases}1, & |x|\leq k \\ \frac{k}{x}, & |x|>k\end{cases}</tex>-->
+
| <tex>\begin{cases}1, & |x|\leq k \\ \frac{k}{x}, & |x|>k\end{cases}</tex>
|-
|-
! "fair"
! "fair"
| <tex>c^2\left(\frac{|x|}{c}-\log\left(1+\frac{|x|}{c}\right)\right)</tex>
| <tex>c^2\left(\frac{|x|}{c}-\log\left(1+\frac{|x|}{c}\right)\right)</tex>
| <tex>\frac{x}{1+\frac{|x|}{c}}</tex>
| <tex>\frac{x}{1+\frac{|x|}{c}}</tex>
-
<!-- | <tex>\frac{1}{1+\frac{|x|}{c}}</tex>-->
+
| <tex>\frac{1}{1+\frac{|x|}{c}}</tex>
|-
|-
! Cauchy
! Cauchy
| <tex>\frac{c}{2}\log\left(1+\left(x/c\right)^2\right)</tex>
| <tex>\frac{c}{2}\log\left(1+\left(x/c\right)^2\right)</tex>
| <tex>\frac{x}{1+\left(x/c\right)^2}</tex>
| <tex>\frac{x}{1+\left(x/c\right)^2}</tex>
-
<!-- | <tex>\frac{1}{1+\left(x/c\right)^2}</tex>-->
+
| <tex>\frac{1}{1+\left(x/c\right)^2}</tex>
|-
|-
! Geman-McClure
! Geman-McClure
| <tex>\frac{x^2/2}{1+x^2}</tex>
| <tex>\frac{x^2/2}{1+x^2}</tex>
| <tex>\frac{x}{\left(1+x^2\right)^2}</tex>
| <tex>\frac{x}{\left(1+x^2\right)^2}</tex>
-
<!-- | <tex>\frac{1}{\left(1+x^2\right)^2}</tex>-->
+
| <tex>\frac{1}{\left(1+x^2\right)^2}</tex>
|-
|-
! Welsch
! Welsch
| <tex>\frac{c^2}{2}\left(1-\exp\left(-\left(x/c\right)^2\right)\right)</tex>
| <tex>\frac{c^2}{2}\left(1-\exp\left(-\left(x/c\right)^2\right)\right)</tex>
| <tex>x\exp\left(-\left(x/c\right)^2\right)</tex>
| <tex>x\exp\left(-\left(x/c\right)^2\right)</tex>
-
<!-- | <tex>\exp\left(-\left(x/c\right)^2\right)</tex>-->
+
| <tex>\exp\left(-\left(x/c\right)^2\right)</tex>
|-
|-
-
! Tukey
+
! [[Взвешенное среднее Тьюки|Tukey]]
| <tex>\begin{cases}\frac{c^2}{6}\left(1-\left(1-\left(x/c\right)^2\right)^3\right), & |x|\leq c \\ \frac{c^2}{6}, & |x|>c \end{cases}</tex>
| <tex>\begin{cases}\frac{c^2}{6}\left(1-\left(1-\left(x/c\right)^2\right)^3\right), & |x|\leq c \\ \frac{c^2}{6}, & |x|>c \end{cases}</tex>
| <tex>\begin{cases}x\left(1\left(x/c\right)^2\right)^2 , & |x|\leq c \\ 0 , & |x|>c \end{cases}</tex>
| <tex>\begin{cases}x\left(1\left(x/c\right)^2\right)^2 , & |x|\leq c \\ 0 , & |x|>c \end{cases}</tex>
-
<!-- | <tex>\begin{cases}\left(1\left(x/c\right)^2\right)^2, & |x|\leq c \\ 0, & |x|>c \end{cases}</tex>-->
+
| <tex>\begin{cases}\left(1\left(x/c\right)^2\right)^2, & |x|\leq c \\ 0, & |x|>c \end{cases}</tex>
|-
|-
! Andrews
! Andrews
| <tex>\begin{cases}k^2\left(1-\cos\left(x/k\right)\right), & |x|\leq k\pi \\ 2k^2, & |x|>k\pi \end{cases}</tex>
| <tex>\begin{cases}k^2\left(1-\cos\left(x/k\right)\right), & |x|\leq k\pi \\ 2k^2, & |x|>k\pi \end{cases}</tex>
| <tex>\begin{cases}k\sin\left(x/k\right), & |x|\leq k\pi \\ 0, & |x|>k\pi \end{cases}</tex>
| <tex>\begin{cases}k\sin\left(x/k\right), & |x|\leq k\pi \\ 0, & |x|>k\pi \end{cases}</tex>
-
<!-- | <tex>\begin{cases}\frac{\sin\left(x/k\right)}{x/k}, & |x|\leq k\pi \\ 0, & |x|>k\pi \end{cases}</tex>-->
+
| <tex>\begin{cases}\frac{\sin\left(x/k\right)}{x/k}, & |x|\leq k\pi \\ 0, & |x|>k\pi \end{cases}</tex>
|}
|}
Следующая таблица содержит значения параметров методов, подобранные таким образом, чтобы при применении к стандартному нормальному распределению оценки имели асимптотическую эффективность 95%.
Следующая таблица содержит значения параметров методов, подобранные таким образом, чтобы при применении к стандартному нормальному распределению оценки имели асимптотическую эффективность 95%.

Текущая версия

М-оценки — широкий класс статистических оценок, доставляющих минимум суммы каких-либо функций от данных:

\hat{\theta}=\arg\min_{\displaystyle\theta}\sum_{i=1}^n\rho\left(x_i, \theta\right) \,\!

М-оценками являются, в частности, оценки наименьших квадратов, а также многие оценки максимального правдоподобия.

Функция \rho выбирается таким образом, чтобы обеспечить желаемые свойства оценки (несмещённость и эффективность) в условиях, когда данные взяты из известного распределения, и достаточную устойчивость к отклонениям от этого распределения.

M-оценки положения распределения

Для положения распределения М-оценки задаются следующим образом:

\hat{\theta}=\arg\min_{\displaystyle\theta}\sum_{i=1}^n\rho\left(x_i - \theta\right), \,\!

где функция \rho должна удовлетворять требованиям

\rho(0)=0, \;\; \rho(x)\geq 0 \forall x, \;\; \rho(-x)=\rho(x), \;\; \rho(x_1)\geq\rho(x_2) при |x_1|>|x_2|.

Среднее и медиана распределения минимизируют, соответственно, функции \sum_{i=1}^n \left(x_i-\theta\right)^2 и \sum_{i=1}^n \left|x_i-\theta\right|; примеры других функций \rho, рассматриваемых в теории робастного оценивания, приведены в таблице ниже.

Если \rho имеет производную \psi, задача минимизации приводит к уравнению

\sum_{i=1}^n \psi\left(x_i-\theta\right)=0.

Чтобы сделать М-оценку независимой от коэффициента масштаба распределения, можно перейти к задаче

\min_{\displaystyle\theta}\sum_{i=1}^n\rho\left(\frac{x_i - \theta}{s}\right), \,\!
\sum_{i=1}^n\psi\left(\frac{x_i - \theta}{s}\right)=0,

где значение параметра s можно находить вместе с \theta, а можно считать в данной задаче известным, используя какую-либо оценку (например, абсолютное отклонение среднего).

Иногда от этой задаче переходят к задаче вида

\sum_{i=1}^n w\left(r_i\right) r_i = 0,

где r_i=\frac{x_i - \theta}{s}, w\left(r_i\right)=\frac{\psi\left(r_i\right)}{r_i} — весовая функция. Оценка параметра тогда получается как решение итерационно перевзвешиваемой задачи наименьших квадратов:

\sum_{i=1}^n w\left(r_i^{(k-1)}\right)r_i^{(k)},

где k — номер итерации.

Вид функции для некоторых популярных М-оценок.
Вид функции \rho для некоторых популярных М-оценок.
М-оценка \rho(x) \psi(x) w(x)
Huber \begin{cases}x^2/2, & |x|\leq k \\ k\left(|x|-k/2\right), & |x|>k \end{cases} \begin{cases}x, & |x|\leq k \\ k\operatorname{sgn}(x), & |x|>k \end{cases} \begin{cases}1, & |x|\leq k \\ \frac{k}{x}, & |x|>k\end{cases}
"fair" c^2\left(\frac{|x|}{c}-\log\left(1+\frac{|x|}{c}\right)\right) \frac{x}{1+\frac{|x|}{c}} \frac{1}{1+\frac{|x|}{c}}
Cauchy \frac{c}{2}\log\left(1+\left(x/c\right)^2\right) \frac{x}{1+\left(x/c\right)^2} \frac{1}{1+\left(x/c\right)^2}
Geman-McClure \frac{x^2/2}{1+x^2} \frac{x}{\left(1+x^2\right)^2} \frac{1}{\left(1+x^2\right)^2}
Welsch \frac{c^2}{2}\left(1-\exp\left(-\left(x/c\right)^2\right)\right) x\exp\left(-\left(x/c\right)^2\right) \exp\left(-\left(x/c\right)^2\right)
Tukey \begin{cases}\frac{c^2}{6}\left(1-\left(1-\left(x/c\right)^2\right)^3\right), & |x|\leq c \\ \frac{c^2}{6}, & |x|>c \end{cases} \begin{cases}x\left(1\left(x/c\right)^2\right)^2 , & |x|\leq c \\ 0 , & |x|>c \end{cases} \begin{cases}\left(1\left(x/c\right)^2\right)^2, & |x|\leq c \\ 0, & |x|>c \end{cases}
Andrews \begin{cases}k^2\left(1-\cos\left(x/k\right)\right), & |x|\leq k\pi \\ 2k^2, & |x|>k\pi \end{cases} \begin{cases}k\sin\left(x/k\right), & |x|\leq k\pi \\ 0, & |x|>k\pi \end{cases} \begin{cases}\frac{\sin\left(x/k\right)}{x/k}, & |x|\leq k\pi \\ 0, & |x|>k\pi \end{cases}

Следующая таблица содержит значения параметров методов, подобранные таким образом, чтобы при применении к стандартному нормальному распределению оценки имели асимптотическую эффективность 95%.

М-оценка Значение параметра
Huber 1.345
"fair" 1.3998
Cauchy 2.3849
Welsch 2.9846
Tukey 4.6851
Andrews 1.339


Ссылки

  • M-estimator - статья из английской Википедии
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%9C-%D0%BE%D1%86%D0%B5%D0%BD%D0%BA%D0%B0»
Личные инструменты