Графические модели (курс лекций)/2012/Задание 4

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск

Anton (Обсуждение | вклад)
(Новая: {{stop| '''Задание находится в разработке.'''<br/> Не приступайте к выполнению задания до его официальной выд...)
К следующему изменению →

Версия 13:25, 7 апреля 2012

Задание находится в разработке.

Не приступайте к выполнению задания до его официальной выдачи.


Содержание

Основная статья: Графические модели (курс лекций)

Начало выполнения задания: 9 апреля 2012

Срок сдачи: 18 апреля 2012, 18.00

Задача 1

Построить граф, минимальный разрез которого соответствует минимизации энергии 1 - x_1 \dots x_n = [x_1 + \dots x_n \neq n] . Здесь x_1,\dots, x_n — бинарные переменные, [\cdot] — скобка Айверсона.

Доказать, что каждый возможный разрез этой конструкции соответствует определенной разметке переменных.

Подсказка: -x_1\dots x_n = \min_z \left( (n-1)z - zx_1 - \dots - zx_n \right) .

Задача 2

Функция f из задачи 2
Функция f из задачи 2

Построить граф, минимальный разрез которого соответствует минимизации энергии f(x_1 + \dots + x_n) . Здесь f(k) = (n - k) / \ell [k > n - \ell] + [k \leq n - \ell] . Здесь x_1,\dots, x_n — бинарные переменные, [\cdot] — скобка Айверсона.

Доказать, что каждый возможный разрез этой конструкции соответствует определенной разметке переменных.

Задача 3

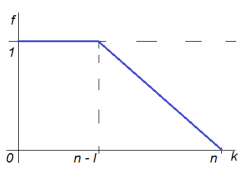
Как при помощи комбинации конструкций из задачи 2 построить конструкцию для минимизации энергии f(x_1 + \dots + x_n) , где f — произвольная вогнутая, кусочно-линейная функция?

Задача 4

Рассмотрим двойственное разложение энергии E(x) = |x_1 - x_2| + |x_2 - x_3| + |x_3 - x_1| на две компоненты: |x_1 - x_2| + |x_2 - x_3| и |x_3 - x_1|. Здесь все переменные бинарны. Построить график двойственной функции. Есть ли зазор между прямой и двойственной задачами? Ответ обосновать.

Задача 5

Рассмотрим двойственное разложение энергии E(x) = |x_1 - x_2| + |x_2 - x_3| + |x_3 - x_4| + |x_4 - x_1| на две компоненты: |x_1 - x_2| + |x_2 - x_3| + |x_3 - x_4| и |x_4 - x_1|. Построить график двойственной функции. Есть ли зазор между прямой и двойственной задачами? Ответ обосновать.


Оформление задания

Выполненный вариант задания необходимо сдать лектору в бумажном виде или прислать на bayesml@gmail.com в электронном виде. Для решения задания можно использовать собственноручно написанные программные средства. Если таковые используются, то их тоже необходимо прислать.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%93%D1%80%D0%B0%D1%84%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B8_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%29/2012/%D0%97%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5_4»
Личные инструменты