|
|
| Строка 3: |
Строка 3: |
| | {{Main|Графические модели (курс лекций)}} | | {{Main|Графические модели (курс лекций)}} |
| | | | |
| - | __TOC__
| + | __NOTOC__ |
| | + | |
| | + | [[Изображение:GM13_task2_intro.jpg|600px]] |
| | | | |
| | '''Начало выполнения задания''': 1 марта 2013 г.<br> | | '''Начало выполнения задания''': 1 марта 2013 г.<br> |
| Строка 10: |
Строка 12: |
| | Среда для выполнения задания — MATLAB. | | Среда для выполнения задания — MATLAB. |
| | | | |
| - | == Вероятностные модели посещаемости курса == | + | == Низкоплотностные коды == |
| - | | + | |
| - | Рассмотрим модель посещаемости студентами одного курса лекции. Пусть аудитория данного курса состоит из студентов профильной кафедры, а также студентов других кафедр. Обозначим через <tex>a</tex> количество студентов, распределившихся на профильную кафедру, а через <tex>b</tex> — количество студентов других кафедр на курсе. Пусть студенты профильной кафедры посещают курс с некоторой вероятностью <tex>p_1</tex>, а студенты остальных кафедр — с вероятностью <tex>p_2</tex>. Обозначим через <tex>c</tex> количество студентов на данной лекции. Тогда случайная величина <tex>c|a,b</tex> есть сумма двух случайных величин, распределенных по биномиальному закону <tex>B(a,p_1)</tex> и <tex>B(b,p_2)</tex> соответственно. Пусть далее на лекции по курсу ведется запись студентов. При этом каждый студент записывается сам, а также, быть может, записывает своего товарища, которого на лекции на самом деле нет. Пусть студент записывает своего товарища с некоторой вероятностью <tex>p_3</tex>. Обозначим через <tex>d</tex> общее количество записавшихся на данной лекции. Тогда случайная величина <tex>d|c</tex> представляет собой сумму <tex>c</tex> и случайной величины, распределенной по биномиальному закону <tex>B(c,p_3)</tex>. Для завершения задания вероятностной модели осталось определить априорные вероятности для <tex>a</tex> и для <tex>b</tex>. Пусть обе эти величины распределены равномерно в своих интервалах <tex>[a_{min},a_{max}]</tex> и <tex>[b_{min},b_{max}]</tex>. Таким образом, мы определили следующую вероятностную модель:<br>
| + | |
| - | '''Модель 1'''<br>
| + | |
| - | {| class = "standard"
| + | |
| - | |-
| + | |
| - | |<tex>p(a,b,c,d)=p(d|c)p(c|a,b)p(a)p(b)</tex>,<br>
| + | |
| - | <tex>d|c \sim c + B(c,p_3)</tex>,<br>
| + | |
| - | <tex>c|a,b \sim B(a,p_1) + B(b,p_2)</tex>,<br>
| + | |
| - | <tex>a \sim R[a_{min},a_{max}]</tex>,<br>
| + | |
| - | <tex>b \sim R[b_{min},b_{max}]</tex>.<br>
| + | |
| - | | [[Изображение:BayesML2010_gm1.png|100px|thumb|Графическая модель для вероятностной модели 1]]
| + | |
| - | |-
| + | |
| - | |}
| + | |
| - | | + | |
| - | <br>Рассмотрим несколько упрощенную версию модели 1. Известно, что биномиальное распределение <tex>B(n,p)</tex> при большом количестве испытаний и маленькой вероятности успеха может быть с высокой точностью приближено пуассоновским распределением <tex>Poiss(\lambda)</tex> с <tex>\lambda = np</tex>. Известно также, что сумма двух пуассоновских распределений с параметрами <tex>\lambda_1</tex> и <tex>\lambda_2</tex> есть пуассоновское распределение с параметром <tex>\lambda_1+\lambda_2</tex>. Таким образом, мы можем сформулировать вероятностную модель, которая является приближенной версией модели 1:<br>
| + | |
| - | '''Модель 2'''<br>
| + | |
| - | <tex>p(a,b,c,d)=p(d|c)p(c|a,b)p(a)p(b)</tex>,<br>
| + | |
| - | <tex>d|c \sim c + B(c,p_3)</tex>,<br>
| + | |
| - | <tex>c|a,b \sim Poiss(ap_1+bp_2)</tex>,<br>
| + | |
| - | <tex>a \sim R[a_{min},a_{max}]</tex>,<br>
| + | |
| - | <tex>b \sim R[b_{min},b_{max}]</tex>.<br>
| + | |
| - | | + | |
| - | <br>Рассмотрим теперь модель посещаемости нескольких лекций курса. Будем считать, что посещаемости отдельных лекций являются независимыми. Тогда:<br>
| + | |
| - | '''Модель 3'''<br>
| + | |
| - | {| class = "standard"
| + | |
| - | |-
| + | |
| - | |<tex>p(a,b,c_1,\dots,c_N,d_1,\dots,d_N)=\prod_{n=1}^Np(d_n|c_n)p(c_n|a,b)p(a)p(b)</tex>,<br>
| + | |
| - | <tex>d_n|c_n \sim c_n + B(c_n,p_3)</tex>,<br>
| + | |
| - | <tex>c_n|a,b \sim B(a,p_1) + B(b,p_2)</tex>,<br>
| + | |
| - | <tex>a \sim R[a_{min},a_{max}]</tex>,<br>
| + | |
| - | <tex>b \sim R[b_{min},b_{max}]</tex>.<br>
| + | |
| - | | [[Изображение:BayesML2010_gm2.png|100px|thumb|Графическая модель для вероятностной модели 3]]
| + | |
| - | |-
| + | |
| - | |}
| + | |
| - | | + | |
| - | <br>По аналогии с моделью 2 можно сформулировать упрощенную модель для модели 3:<br>
| + | |
| - | '''Модель 4'''<br>
| + | |
| - | <tex>p(a,b,c_1,\dots,c_N,d_1,\dots,d_N)=\prod_{n=1}^Np(d_n|c_n)p(c_n|a,b)p(a)p(b)</tex>,<br>
| + | |
| - | <tex>d_n|c_n \sim c_n + B(c_n,p_3)</tex>,<br>
| + | |
| - | <tex>c_n|a,b \sim Poiss(ap_1+bp_2)</tex>,<br>
| + | |
| - | <tex>a \sim R[a_{min},a_{max}]</tex>,<br>
| + | |
| - | <tex>b \sim R[b_{min},b_{max}]</tex>.<br>
| + | |
| - | | + | |
| - | <br>Задание состоит из трех вариантов. Распределение студентов по вариантам см. [[Графические модели (курс лекций)/2013/Задание 1#Распределение студентов по вариантам|ниже]].
| + | |
| - | | + | |
| - | == Вариант 1 ==
| + | |
| - | Рассматривается модель 2 с параметрами <tex>a_{min}=15, a_{max}=30, b_{min}=250, b_{max}=350, p_1 = 0.5, p_2 = 0.05, p_3 = 0.5</tex>. Провести на компьютере следующие исследования:
| + | |
| - | # Найти математические ожидания и дисперсии априорных распределений для всех параметров <tex>a, b, c, d</tex>.
| + | |
| - | # Пронаблюдать, как происходит уточнение прогноза для величины <tex>c</tex> по мере прихода новой косвенной информации. Для этого построить графики и найти мат.ожидание и дисперсию для распределений <tex>p(c), p(c|b), p(c|a,b), p(c|a,b,d)</tex> при параметрах <tex>a,b,d</tex>, равных мат.ожиданиям своих априорных распределений, округленных до ближайшего целого.
| + | |
| - | # Определить, какая из величин <tex>a,b,d</tex> вносит больший вклад в уточнение прогноза для величины <tex>c</tex> (в смысле дисперсии распределения). Для этого убедиться в том, что <tex>\mathbb{D}[c|d]<\mathbb{D}[c|b]</tex> и <tex>\mathbb{D}[c|d]<\mathbb{D}[c|a]</tex> для любых допустимых значений <tex>a,b,d</tex>. Найти множество точек <tex>(a,b)</tex> таких, что <tex>\mathbb{D}[c|b]<\mathbb{D}[c|a]</tex>. Являются ли множества <tex>\{(a,b)|\mathbb{D}[c|b]<\mathbb{D}[c|a]\}</tex> и <tex>\{(a,b)|\mathbb{D}[c|b]\ge\mathbb{D}[c|a]\}</tex> линейно разделимыми?
| + | |
| - | # Провести временные замеры по оценке всех необходимых распределений <tex>p(c),p(c|a),p(c|b),p(c|d),p(c|a,b),p(c|a,b,d),p(d)</tex>.
| + | |
| - | # Провести исследования из пп. 1-4 для точной модели 1 и сравнить результаты с аналогичными для модели 2. Привести пример оценки параметра, в котором разница между моделью 1 и 2 проявляется в большой степени.
| + | |
| - | | + | |
| - | Взять в качестве диапазона допустимых значений для величины <tex>c</tex> интервал <tex>[0,a_{max}+b_{max}]</tex>, а для величины <tex>d</tex> — интервал <tex>[0,2*(a_{max}+b_{max})]</tex>.
| + | |
| - | | + | |
| - | При оценке выполнения задания будет учитываться эффективность программного кода. В частности, временные затраты на расчет отдельного распределения не должны превышать одной секунды.
| + | |
| - | | + | |
| - | == Вариант 2 ==
| + | |
| - | Рассматривается модель 2 с параметрами <tex>a_{min}=15, a_{max}=30, b_{min}=250, b_{max}=350, p_1 = 0.5, p_2 = 0.05, p_3 = 0.5</tex>. Провести на компьютере следующие исследования:
| + | |
| - | # Найти математические ожидания и дисперсии априорных распределений для всех параметров <tex>a, b, c, d</tex>.
| + | |
| - | # Пронаблюдать, как происходит уточнение прогноза для величины <tex>b</tex> по мере прихода новой косвенной информации. Для этого построить графики и найти мат.ожидание и дисперсию для распределений <tex>p(b), p(b|a), p(b|a,d)</tex> при параметрах <tex>a,d</tex>, равных мат.ожиданиям своих априорных распределений, округленных до ближайшего целого.
| + | |
| - | # Определить, при каких соотношениях параметров <tex>p_1,p_2</tex> изменяется относительная важность параметров <tex>a,b</tex> для оценки величины <tex>c</tex>. Для этого найти множество точек <tex>\{(p_1,p_2)|\mathbb{D}[c|b]<\mathbb{D}[c|a]\}</tex> при <tex>a,b</tex>, равных мат.ожиданиям своих априорных распределений, округленных до ближайшего целого. Являются ли множества <tex>\{(p_1,p_2)|\mathbb{D}[c|b]<\mathbb{D}[c|a]\}</tex> и <tex>\{(p_1,p_2)|\mathbb{D}[c|b]\ge\mathbb{D}[c|a]\}</tex> линейно разделимыми?
| + | |
| - | # Провести временные замеры по оценке всех необходимых распределений <tex>p(c),p(c|a),p(c|b),p(b|a),p(b|a,d),p(d)</tex>.
| + | |
| - | # Провести исследования из пп. 1-4 для точной модели 1 и сравнить результаты с аналогичными для модели 2. Привести пример оценки параметра, в котором разница между моделью 1 и 2 проявляется в большой степени.
| + | |
| - | | + | |
| - | Взять в качестве диапазона допустимых значений для величины <tex>c</tex> интервал <tex>[0,a_{max}+b_{max}]</tex>, а для величины <tex>d</tex> — интервал <tex>[0,2*(a_{max}+b_{max})]</tex>.
| + | |
| - | | + | |
| - | При оценке выполнения задания будет учитываться эффективность программного кода. В частности, временные затраты на расчет отдельного распределения не должны превышать одной секунды.
| + | |
| - | | + | |
| - | == Вариант 3 ==
| + | |
| - | Рассматривается модель 4 с параметрами <tex>a_{min}=15, a_{max}=30, b_{min}=250, b_{max}=350, p_1 = 0.5, p_2 = 0.05, p_3 = 0.5, N = 50</tex>. Провести на компьютере следующие исследования:
| + | |
| - | # Найти математические ожидания и дисперсии априорных распределений для всех параметров <tex>a, b, c_n, d_n</tex>.
| + | |
| - | # Реализовать генератор выборки <tex>d_1,\dots,d_N</tex> из модели при заданных значениях параметров <tex>a,b</tex>.
| + | |
| - | # Пронаблюдать, как происходит уточнение прогноза для величины <tex>b</tex> по мере прихода новой косвенной информации. Для этого построить графики и найти мат.ожидание и дисперсию для распределений <tex>p(b), p(b|d_1), \dots, p(b|d_1,\dots,d_N)</tex>, где выборка <tex>d_1,\dots,d_N</tex> 1) сгенерирована из модели при параметрах <tex>a,b</tex>, равных мат.ожиданиям своих априорных распределений, округленных до ближайшего целого и 2) <tex>d_1=\dots=d_N</tex>, где <tex>d_n</tex> равно мат.ожиданию своего априорного распределения, округленного до ближайшего целого. Провести аналогичный эксперимент, если дополнительно известно значение <tex>a</tex>. Сравнить результаты двух экспериментов.
| + | |
| - | # Провести временные замеры по оценке всех необходимых распределений <tex>p(c_n),p(d_n),p(b|d_1,\dots,d_n),p(b|a,d_1,\dots,d_n)</tex>.
| + | |
| - | # Провести исследования из пп. 1-4 для точной модели 3 и сравнить результаты с аналогичными для модели 4.
| + | |
| - | | + | |
| - | Взять в качестве диапазона допустимых значений для величины <tex>c</tex> интервал <tex>[0,a_{max}+b_{max}]</tex>, а для величины <tex>d</tex> — интервал <tex>[0,2*(a_{max}+b_{max})]</tex>.
| + | |
| | | | |
| - | При оценке выполнения задания будет учитываться эффективность программного кода. В частности, временные затраты на расчет отдельного распределения не должны превышать одной секунды.
| + | == Формулировка задания == |
| | | | |
| | == Оформление задания == | | == Оформление задания == |
| | | | |
| - | Выполненное задание следует отправить письмом по адресу ''bayesml@gmail.com'' с заголовком письма «[ГМ13] Задание 1 <ФИО>». Убедительная просьба присылать выполненное задание '''только один раз''' с окончательным вариантом. Также убедительная просьба строго придерживаться заданных ниже прототипов реализуемых функций. | + | Выполненное задание следует отправить письмом по адресу ''bayesml@gmail.com'' с заголовком письма «[ГМ13] Задание 2 <ФИО>». Убедительная просьба присылать выполненное задание '''только один раз''' с окончательным вариантом. Также убедительная просьба строго придерживаться заданных ниже прототипов реализуемых функций. |
| | | | |
| | Присланный вариант задания должен содержать в себе: | | Присланный вариант задания должен содержать в себе: |
| - | * Текстовый файл в формате PDF с указанием ФИО и номера варианта, содержащий описание всех проведенных исследований. | + | * Текстовый файл в формате PDF с указанием ФИО, содержащий описание всех проведенных исследований. |
| | * Все исходные коды с необходимыми комментариями. | | * Все исходные коды с необходимыми комментариями. |
| | | | |
| Строка 159: |
Строка 83: |
| | |d — значения <tex>d_1,\dots,d_N</tex>, вектор-столбец длины N. | | |d — значения <tex>d_1,\dots,d_N</tex>, вектор-столбец длины N. |
| | |} | | |} |
| - | |}
| |
| - |
| |
| - | == Распределение студентов по вариантам ==
| |
| - |
| |
| - | {|class = "standard sortable"
| |
| - | ! class="unsortable"|№ п/п !! Студент !! Вариант
| |
| - | |-
| |
| - | | align="center"|1 || Березин Алексей Андреевич || 1
| |
| - | |-
| |
| - | | align="center"|2 || [[Участник:Borman|Борисов Михаил Викторович]] || 3
| |
| - | |-
| |
| - | | align="center"|3 || Гавриков Михаил Игоревич || 3
| |
| - | |-
| |
| - | | align="center"|4 || Зак Евгений Михайлович || 3
| |
| - | |-
| |
| - | | align="center"|5 || Исмагилов Тимур Ниязович || 2
| |
| - | |-
| |
| - | | align="center"|6 || Кондрашкин Дмитрий Андреевич || 1
| |
| - | |-
| |
| - | | align="center"|7 || [[Участник:Kuraga|Куракин Александр Владимирович]] || 1
| |
| - | |-
| |
| - | | align="center"|8 || Лобачева Екатерина Максимовна || 2
| |
| - | |-
| |
| - | | align="center"|9 || Любимцева Мария Михайловна || 2
| |
| - | |-
| |
| - | | align="center"|10 || Малышева Екатерина Константиновна || 1
| |
| - | |-
| |
| - | | align="center"|11 || Морозова Дарья Юрьевна || 2
| |
| - | |-
| |
| - | | align="center"|12 || [[Участник:Nizhibitsky|Нижибицкий Евгений Алексеевич]] || 2
| |
| - | |-
| |
| - | | align="center"|13 || [[Участник:Novikov|Новиков Максим Сергеевич]] || 3
| |
| - | |-
| |
| - | | align="center"|14 || Огнева Дарья Сергеевна || 2
| |
| - | |-
| |
| - | | align="center"|15 || [[Участник:MoRandi91|Остапец Андрей Александрович]] || 3
| |
| - | |-
| |
| - | | align="center"|16 || Потапенко Анна Александровна || 1
| |
| - | |-
| |
| - | | align="center"|17 || [[Участник:Peter Romov|Ромов Петр Алексеевич]] || 1
| |
| - | |-
| |
| - | | align="center"|18 || [[Участник:Newo|Фонарев Александр Юрьевич]] || 1
| |
| - | |-
| |
| - | | align="center"|19 || Шаймарданов Ильдар Рифарович || 3
| |
| - | |-
| |
| | |} | | |} |
Среда для выполнения задания — MATLAB.
Исходные коды должны включать в себя реализацию оценки распределений в виде отдельных функций. Прототип для функции оценки распределения ) для модели 2 имеет следующий вид:
для модели 2 имеет следующий вид:
Прототипы функций для других распределений выглядят аналогично. Если в распределении переменных до или после | несколько, то в названии функции они идут в алфавитном порядке. Функция для оценки распределения ) для модели 3 имеет название p3b_ad, а входной параметр
для модели 3 имеет название p3b_ad, а входной параметр 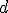 является одномерным массивом длины
является одномерным массивом длины 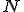 .
.
для модели 2 имеет следующий вид:
для модели 3 имеет название p3b_ad, а входной параметр
является одномерным массивом длины
.