Графические модели (курс лекций)/2013/Задание 2

Материал из MachineLearning.

(Различия между версиями)

Версия 17:21, 3 марта 2013

Формулировка задания находится в стадии разработки. Убедительная просьба не приступать к выполнению задания до тех пор, пока это предупреждение не будет удалено.

Основная статья: Графические модели (курс лекций)

Демонстрация процесса кодирования/декодирования с исправлением ошибок. Кодируемое сообщение (изображение цифры) содержит значительную избыточность для возможности визуальной оценки процесса декодирования. Алгоритм декодирования не использует свойство избыточности входного сигнала.

Начало выполнения задания: 3 марта 2013 г.
Срок сдачи: 17 марта 2013 г., 23:59.

Среда для выполнения задания — MATLAB.

Низкоплотностные коды

Фактор-граф для (16,4)-низкоплотностного кода, в проверочной матрице которого в каждом столбце по 3 единицы, а в каждой строке - по 4 единицы.

Низкоплотностный код (или код с малой плотностью проверок на чётность) представляет собой бинарный линейный (N,K)-блоковый код, в котором проверочная матрица $H\in\{0,1\}^{(N-K)\times N}$ является сильно разреженной. Таким образом, вектор $x\in\{0,1\}^N$ является кодовым словом, если $Hx = 0$ (здесь и далее все вычисления проводятся по модулю 2).

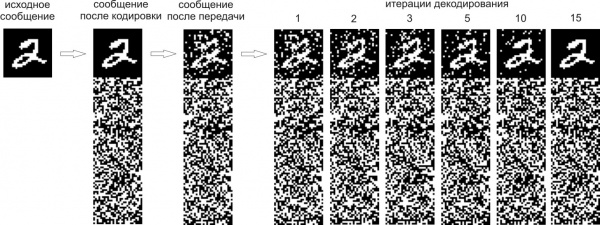
Рассмотрим бинарный симметричный канал для передачи данных. Здесь при передаче каждый бит независимо инвертируется с некоторой вероятностью q. В результате бинарный симметричный канал задает распределение $p(y|x)$ для передаваемого кодового слова $x\in\{0,1\}^N$ и полученного на выходе слова $y\in\{0,1\}^N$ как

$p(y|x) = \prod_{n=1}^Np(y_n|x_n) = \prod_{n=1}^Nq^{y_n+x_n}(1-q)^{y_n+x_n+1}$ .

Пропускная способность данного канала определяется величиной $1+q\log_2q+(1-q)\log_2(1-q)$ .

Объединяя низкоплотностный код с бинарным симметричным каналом, получаем следующую вероятностную модель для пары $x,y$ :

$p(y,x)\propto p(y|x)I[Hx=0] = \prod_{n=1}^Np(y_n|x_n)\prod_{m=1}^MI[h_m^Tx = 0]$ .

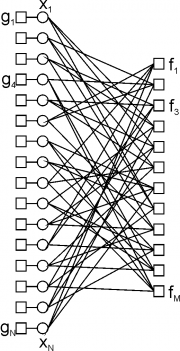
Здесь M=N-K — количество проверок на чётность, $h_m^T$ — m-ая строка матрицы H, а $I[\cdot]$ — индикаторная функция. Фактор-граф введённой модели показан на рис. справа.

Восстановление кодового слова $x$ по полученному слову $y$ предлагается осуществлять как $x_n^* = \arg\max p(x_n|y)$ , а маргинальные распределения $p(x_n|y)$ оценивать в помощью циклического алгоритма передачи сообщений (sum-product loopy BP) на фактор-графе. При этом для упрощения алгоритма декодирования предлагается избавиться от факторов-унарных потенциалов (путем их включения в сообщения от переменных $x_n$ к факторам $f_m$ ), а в качестве расписания пересчёта сообщений выбрать параллельное расписание, при котором сначала все переменные одновременно посылают сообщения во все факторы, а затем все факторы одновременно посылают сообщения во все вершины.

Введём обозначения $N(n)=\{m:H_{mn}=1\}$ — множество факторов, в которых участвует переменная $x_n$ , и $N(m)=\{n:H_{mn}=1\}$ — множество переменных, которые входят в фактор $f_m$ . Тогда общая схема алгоритма декодирования выглядит следующим образом:

1. Инициализация:

$\mu_{x_n\rightarrow f_m}(x_n) = p(y_n|x_n)$ ;

2. Пересчет сообщений от факторов:

$\mu_{f_m\rightarrow x_n}(x_n) = \sum_{x_{n^'}:n^'\in N(m)\backslash n}I[x_n+\sum_{n^'}x_{n^'}=0]\prod_{n^'\in N(m)\backslash n}\mu_{x_{n^'}\rightarrow f_m}(x_{n^'})$ ;

3. Пересчет сообщений от переменных:

$\mu_{x_n\rightarrow f_m}(x_n) \propto p(y_n|x_n)\prod_{m^'\in N(n)\backslash m}\mu_{f_{m^'}\rightarrow x_n}(x_n)$ ;

$\hat{p}_n(x_n|y)\propto p(y_n|x_n)\prod_{m^'\in N(n)}\mu_{f_{m^'}\rightarrow x_n}(x_n)$ ;

Символом $\propto$ обозначается пропорциональность. Таким образом, при пересчете все сообщения от переменных и оценки на маргинальные распределения должны нормироваться так, чтобы $\mu_{x_n\rightarrow f_m}(0)+\mu_{x_n\rightarrow f_m}(1)=1$ и $\hat{p}_n(0|y)+\hat{p}_n(1|y)=1$ ;

4. Оценка кодового слова:

$\hat{x}_n=\arg\max\hat{p}_n(x_n|y)$ ;

5. Критерий остановки:

Если $H\hat{x}=0$ , то выход алгоритма со статусом 0;

Если достигнуто максимальное число итераций или суммарная норма разности между сообщениями на текущей и предыдущей итерациях меньше определенного порога $\varepsilon$ , то выход алгоритма со статусом -1;

Переход к шагу 2.

При прямой реализации данного алгоритма на шаге 2 требуется рассмотрение для каждого фактора $2^{N(m)-1}$ различных конфигураций переменных. Это может приводить как к низкой скорости пересчета сообщений, так и к большим требованиям по памяти.

Рассмотрим более эффективную схему реализации шага 2 путем его сведения к задаче вывода в графической модели с графом-цепочкой. Пусть нам необходимо вычислить сообщение $\mu_{f_m\rightarrow x_n}(x_n)$ . Перенумеруем все переменные, входящие в m-ый фактор (кроме переменной $x_n$ ), как $x_1,x_2,\dots,x_{N(m)-1}$ . Рассмотрим графическую модель с $N(m)-1$ бинарными переменными $s_i$ и графом

Положим, что $s_i=\sum_{j=1}^ix_j$ . Определим априорное распределение и вероятность перехода как

$p(s_1) = \mu_{x_1\rightarrow f_m}(s_1)$ ; $p(s_i|s_{i-1}) = \begin{cases}\mu_{x_i\rightarrow f_m}(0),& s_i=s_{i-1},\\ \mu_{x_i\rightarrow f_m}(1),& s_i\neq s_{i-1}.\end{cases}$

Тогда требуемое сообщение $\mu_{f_m\rightarrow x_n}(x_n)$ поэлементно равно маргинальному распределению $p(s_{N(m)-1})$ , которое может быть эффективно вычислено путем однократной пересылки сообщений вдоль цепи от $s_1$ до $s_{N(m)-1}$ .

Дальнейшее повышение эффективности реализации шага 2 связано с рассмотрением разностей значений сообщений $\delta\mu_{x_n\rightarrow f_m} = \mu_{x_n\rightarrow f_m}(0) - \mu_{x_n\rightarrow f_m}(1)$ и $\delta\mu_{f_m\rightarrow x_n} = \mu_{f_m\rightarrow x_n}(0) - \mu_{f_m\rightarrow x_n}(1)$ . В терминах разностей можно показать, что новое значение $\delta\mu_{f_m\rightarrow x_n}$ может быть вычислено как

$\delta\mu_{f_m\rightarrow x_n} = \prod_{n^'\in N(m)\backslash n}\delta\mu_{x_{n^'}\rightarrow f_m}$ . (*)

Зная значение $\delta\mu_{f_m\rightarrow x_n}$ и учитывая условие нормировки на сообщения, сами сообщения от факторов могут быть вычислены как

$\mu_{f_m\rightarrow x_n}(0) = \frac{1}{2}(1+\delta\mu_{f_m\rightarrow x_n})$ ; $\mu_{f_m\rightarrow x_n}(1) = \frac{1}{2}(1-\delta\mu_{f_m\rightarrow x_n})$ .

Основное преимущество условия (*) по сравнению с пересчетом сообщений для $s_i$ связано с тем, что формула (*) может быть реализована с помощью векторных операций в MATLAB.

Покажем теперь справедливость условия (*). Для этого рассмотрим две произвольные бинарные независимые случайные величины $u_1$ и $u_2$ . Обозначим через $p_i^u$ величину $\mathbb{P}\{u_i=u\}$ . Тогда очевидно, что

$\mathbb{P}\{u_1+u_2=0\} = p_1^0p_2^0 + p_1^1p_2^1$ ; $\mathbb{P}\{u_1+u_2=1\} = p_1^0p_2^1 + p_1^1p_2^0$ ; $\mathbb{P}\{u_1+u_2=0\}-\mathbb{P}\{u_1+u_2=1\} = (p_1^0-p_1^1)(p_2^0-p_2^1) = \delta p_1\delta p_2$ .

Аналогичные рассуждения справедливы для произвольного количества случайных величин $u$ . В частности,

$\mathbb{P}\{u_1+u_2+u_3=0\} - \mathbb{P}\{u_1+u_2+u_3=1\} = \delta p_1\delta p_2\delta p_3$ .

Отсюда немедленно следует справедливость (*).

Формулировка задания

Реализовать алгоритм построения по заданной проверочной матрице чётности H порождающей матрицы кода G для систематического кодирования;
Реализовать алгоритм декодирования низкоплотностного кода на основе loopy BP; при реализации шага 2 пересчета сообщений от факторов к переменным необходимо использовать эффективные схемы, обозначенные выше; при реализации на MATLAB одной итерации схемы передачи сообщений использование вложенных циклов является нежелательным; провести временные замеры реализованного алгоритма для различных значений входных параметров;
Рассмотрим две характеристики качества кода — вероятность совершить ошибку хотя бы в одном бите при декодировании блока ( $p(\hat{x}\neq x)$ ) и среднюю вероятность совершить ошибку при декодировании в одном бите ( $\frac{1}{N}\sum_{n=1}^Np(\hat{x}_n\neq x_n)$ ). Требуется реализовать алгоритм оценки вероятности битовой и блоковой ошибки кода с помощью метода стат. испытаний (многократная случайная генерация слова $t$ , его преобразование к кодовому слову $x$ , передача по каналу с независимым инвертированием каждого бита с заданной вероятностью $q$ , восстановление кодового слова $\hat{x}$ с помощью алгоритма декодирования и подсчет необходимых характеристик);
Провести эксперименты по оцениванию битовой и блоковой ошибки низкоплотностного кода для различных значений длины кодового слова N, скорости кода R, вероятности инвертирования бита при передаче по каналу связи q и среднего количества единиц в столбце проверочной матрицы j. В частности, необходимо проанализировать следующие ситуации:
- Теорема Шеннона определяет пропускную способность канала как максимально допустимую скорость кода, при которой возможно осуществление надежной коммуникации. Требуется проверить, как меняются характеристики кода при изменении скорости R от минимального значения до пропускной способности канала.
- Теорема Шеннона предполагает, что качество кода растет при увеличении длины кодового слова N. Требуется проверить это предположение.
- Одно из следствий теоремы Шеннона утверждает, что хорошими кодами являются коды со случайной проверочной матрицей H. В частности, здесь предполагается, что качество кода должно расти при увеличении среднего количества единиц в столбце проверочной матрицы j. Требуется проверить это утверждение для низкоплотностных кодов.

Оформление задания

Выполненное задание следует отправить письмом по адресу bayesml@gmail.com с заголовком письма «[ГМ13] Задание 2 <ФИО>». Убедительная просьба присылать выполненное задание только один раз с окончательным вариантом. Также убедительная просьба строго придерживаться заданных ниже прототипов реализуемых функций.

Присланный вариант задания должен содержать в себе:

Текстовый файл в формате PDF с указанием ФИО, содержащий описание всех проведенных исследований. Данный файл должен, в частности, содержать необходимые графики зависимости битовой и блоковой ошибки кода в зависимости от различных значений параметров.
Все исходные коды с необходимыми комментариями.

Построение порождающей матрицы для систематического кодирования

[G, ind] = ldpc_gen_matrix(H)

ВХОД

H — проверочная матрица чётности, бинарная матрица размера MxN;

ВЫХОД

G — порождающая матрица кода, бинарная матрица размера Nx(N-M);

ind — номера позиций кодового слова, в которые копируются биты исходного сообщения, т.е. G(ind, :) является единичной матрицей.

Алгоритм декодирования LDPC-кода в синдромном представлении

[e, status] = ldpc_decoding(z, H, q, param_name1, param_value1, ...)

ВХОД

z — наблюдаемый синдром, бинарный вектор-столбец длины M;

H — проверочная матрица чётности, бинарная матрица размера MxN;

q — вероятность инверсии бита при передаче по каналу связи, число от 0 до 0.5;

(param_name, param_value) — набор необязательных параметров алгоритма, следующие имена и значения возможны:

'max_iter' — максимальное число итераций алгоритма декодирования, число, по умолчанию = 200;

'eps' — порог стабилизации для сообщений, число, по умолчанию = 1e-4;

'display' — режим отображения, true или false, если true, то отображается промежуточная информация на итерациях, например, номер итерации, текущее число ошибок декодирования, невязка для сообщений и т.д.

ВЫХОД

e — восстановленный вектор ошибок, бинарный вектор-столбец длины N;

status — результат декодирования, равен 0, если вектор e восстановлен без ошибок, равен -1, если произошел выход по максимальному числу итераций или стабилизации значений сообщений.

Оценка характеристик LDPC-кода с помощью метода Монте Карло

[err_bit, err_block, diver] = ldpc_mc(H, G, q, num_points)

ВХОД

H — проверочная матрица чётности, бинарная матрица размера MxN;

G — порождающая матрица кода, бинарная матрица размера Nx(N-M);

q — вероятность инверсии бита при передаче по каналу связи, число от 0 до 0.5;

num_points — общее количество экспериментов, число;

ВЫХОД

err_bit — вероятность битовой ошибки декодирования (относительно N бит кодового слова), число от 0 до 1;

err_block — вероятность блоковой ошибки декодирования, число от 0 до 1;

diver — доля ситуаций расходимости алгоритма декодирования, число от 0 до 1.

Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%93%D1%80%D0%B0%D1%84%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B8_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%29/2013/%D0%97%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5_2»

@@ Строка 92: / Строка 92: @@
 . Алгоритм декодирования удобно реализовывать в т.н. синдромном представлении. Полученное на выходе канала слово <tex>y</tex> можно представить как <tex>x+e</tex>, где <tex>x</tex> — посылаемое кодовое слово, а <tex>e\in\{0,1\}^N</tex> — вектор ошибок, которые вносит канал. Назовём величину <tex>z = Hy</tex> синдромом полученного сообщения. Тогда <tex>z=Hy=H(x+e)=He</tex>, и на этапе декодирования можно вместо <tex>x</tex> оценивать вектор ошибок <tex>e</tex> путем оценки аргмаксимумов маргинальных распределений <tex>p(e_n|z)</tex> в вероятностной модели
 ::<tex>p(e,z)\propto p(e)I[He=z]=\prod_{n=1}^Np(e_n)\prod_{m=1}^MI[h_m^Te=z_m]</tex>.
-Зная <tex>e</tex>, искомое кодовое слово можно найти как <tex>x=y+e</tex>. Заметим, что реализация алгоритма декодирования в синдромном представлении избавляет от необходимости предварительной реализации алгоритма кодирования.
+Для бинарного симметричного канала <tex>p(e_n) = q^{e_n}(1-q)^{e_n+1}</tex>. Зная <tex>e</tex>, искомое кодовое слово можно найти как <tex>x=y+e</tex>. Заметим, что реализация алгоритма декодирования в синдромном представлении избавляет от необходимости предварительной реализации алгоритма кодирования.
 . При тестировании алгоритма декодирования рекомендуется пробовать запускать итерационный процесс из различных начальных приближений для сообщений (не только из значений унарных потенциалов). При корректной реализации метода должна наблюдаться сходимость к одним и тем же финальным сообщениям независимо от начальных приближений.

Графические модели (курс лекций)/2013/Задание 2

Материал из MachineLearning.

Версия 17:21, 3 марта 2013

Низкоплотностные коды

Формулировка задания

Рекомендации по выполнению задания

Оформление задания

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты