Участник:Vitsemgol/Биномиальное распределение одной случайной величины

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(Новая: {{Вероятностное распределение| name =Биномиальное распределение| type =Функция| pdf_image =[[Изображе...)
(→Основные свойства)
Строка 34: Строка 34:
*Дисперсия: <tex>DX=np(1-p).</tex>
*Дисперсия: <tex>DX=np(1-p).</tex>
*[[Асимметрия]]: <tex>\gamma_1=\frac{1-2p}{\sqrt{np(1-p)}};</tex> при <tex>p=0.5</tex> распределение симметрично относительно центра <tex>n/2.</tex>
*[[Асимметрия]]: <tex>\gamma_1=\frac{1-2p}{\sqrt{np(1-p)}};</tex> при <tex>p=0.5</tex> распределение симметрично относительно центра <tex>n/2.</tex>
 +
 +
==Асимптотические приближения при больших <tex>n</tex>==
 +
 +
Если значения <tex>n</tex> велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно.
 +
В этих случаях можно использовать приближения биномиального распределения распределением Пуассона и нормальным (приближение Муавра-Лапласа).
 +
 +
===Приближение Пуассона===
 +
Приближение [[распределение Пуассона|распределением Пуассона]] применяется в ситуациях, когда значения <tex>n</tex> большие, а значения <tex>p</tex> близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром <tex>\lambda=np.</tex>
 +
 +
Строгая формулировка: если <tex>n\to\infty</tex> и <tex>p\to 0</tex> таким образом, что <tex>np\to\lambda,</tex> то
 +
 +
::<tex>P(X=k)\to\frac{\lambda^k}{k!}e^{-\lambda},\quad k=0, 1, 2, \ldots</tex>
 +
 +
Более того, справедлива следующая оценка. Пусть <tex>Y</tex> &mdash; случайная величина, имеющая распределение Пуассона с параметром <tex>\lambda=np.</tex>
 +
Тогда для произвольного множества <tex>B\subset\{0,1,2,\ldots\}</tex> справедливо неравенство:
 +
 +
::<tex>|P(X\in B) - P(Y\in B)|\le 2np^2.</tex>

Версия 06:58, 15 ноября 2013

Биномиальное распределение
Функция вероятности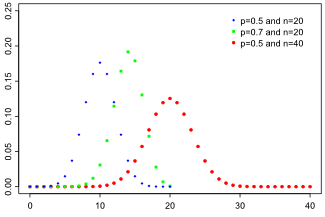
Функция распределения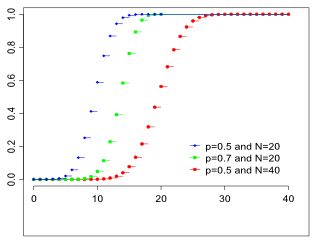
Параметры n \geq 0 — число «испытаний»
0\leq p \leq 1 — вероятность «успеха»
Носитель k \in \{0,\ldots,n\}\!
Функция вероятности {n \choose k}\,p^k q^{n-k} \!
Функция распределения I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) \!
Математическое ожидание np\!
Медиана одно из \{[np]-1, [np], [np]+1\}
Мода \lfloor (n+1)\,p\rfloor\!
Дисперсия npq\!
Коэффициент асимметрии \frac{1-2p}{\sqrt{npq}}\!
Коэффициент эксцесса \frac{1-6pq}{npq}\!
Информационная энтропия \frac12 \log_2 \big( 2\pi e\, np(1-p) \big) + O \left( \frac{1}{n} \right)
Производящая функция моментов (q + pe^t)^n \!
Характеристическая функция (q + pe^{it})^n \!


Содержание

Определение

Биномиальное распределение — дискретное распределение вероятностей одной случайной величины X, принимающей целочисленные значения k=0,1,\ldots,n с вероятностями:

P(X=k)={n \choose k}p^k(1-p)^{n-k}.

Данное распределение характеризуется двумя параметрами: целым числом n>0, называемым числом испытаний, и вещественным числом p, 0\le p\le 1, называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из n независимых испытаний, в каждом из которых может произойти "успех" с вероятностью p, то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы X=X_1+\cdots+X_n независимых слагаемых, имеющих распределение Бернулли.

Основные свойства

Характеристическая функция: \phi(t)=(1+p(e^{it}-1))^n.

Моменты:

  • Математическое ожидание: MX=np.
  • Дисперсия: DX=np(1-p).
  • Асимметрия: \gamma_1=\frac{1-2p}{\sqrt{np(1-p)}}; при p=0.5 распределение симметрично относительно центра n/2.

Асимптотические приближения при больших 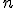n

Если значения n велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно. В этих случаях можно использовать приближения биномиального распределения распределением Пуассона и нормальным (приближение Муавра-Лапласа).

Приближение Пуассона

Приближение распределением Пуассона применяется в ситуациях, когда значения n большие, а значения p близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром \lambda=np.

Строгая формулировка: если n\to\infty и p\to 0 таким образом, что np\to\lambda, то

P(X=k)\to\frac{\lambda^k}{k!}e^{-\lambda},\quad k=0, 1, 2, \ldots

Более того, справедлива следующая оценка. Пусть Y — случайная величина, имеющая распределение Пуассона с параметром \lambda=np. Тогда для произвольного множества B\subset\{0,1,2,\ldots\} справедливо неравенство:

|P(X\in B) - P(Y\in B)|\le 2np^2.
Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:Vitsemgol/%D0%91%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BE%D0%B4%D0%BD%D0%BE%D0%B9_%D1%81%D0%BB%D1%83%D1%87%D0%B0%D0%B9%D0%BD%D0%BE%D0%B9_%D0%B2%D0%B5%D0%BB%D0%B8%D1%87%D0%B8%D0%BD%D1%8B»
Личные инструменты