ДСМ-метод в терминах АФП

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→ДСМ-метод)
(→ДСМ-метод в терминах АФП)
Строка 24: Строка 24:
[Кузнецов 1996], [Ganter, Kuznetsov 2000]
[Кузнецов 1996], [Ganter, Kuznetsov 2000]
 +
В данном разделе приводится формулировка одной из версий ДСМ-метода в терминах [[Анализ формальных понятий|Анализа формальных понятий]]
Помимо признаков из множества <tex>M</tex> имеется ''целевой признак'' <tex>w\notin M</tex>,
Помимо признаков из множества <tex>M</tex> имеется ''целевой признак'' <tex>w\notin M</tex>,

Версия 20:51, 22 декабря 2013

Содержание

ДСМ-метод

Одной из первых моделей машинного обучения, неявно использовавших решетки (системы замыканий или семейства Мура) был ДСМ-метод, предложенный впервые в


В. К. Финн, О машинно-ориентированной формализации правдоподобных рассуждений в стиле Ф. Бэкона -- Д.С. Милля \\ Семиотика и Информатика, 20(1983), 35-10


Метод сходства (Первое правило индуктивной логики):

"Если два или большее число примеров исследуемого явления обладают только одним общим признаком, то ... [этот признак] есть причина (или следствие) данного явления."

John Stuart Mill, A System of Logic, Ratiocinative and Inductive, London, 1843

В ДСМ-методе гипотезы относительно причины явления ищутся среди пересечений описаний положительных примеров явления. На пересечения могут быть наложены различные дополнительные условия.


Логические средства ДСМ-метода представляют собой многозначное многосортное расширение логики предикатов первого порядка с помощью кванторов по кортежам переменной длины (слабая логика предикатов второго порядка).

ДСМ-метод в терминах АФП

[Кузнецов 1996], [Ganter, Kuznetsov 2000]

В данном разделе приводится формулировка одной из версий ДСМ-метода в терминах Анализа формальных понятий

Помимо признаков из множества M имеется целевой признак w\notin M, относительно которого все объекты разделяются следующим образом:

  1. положителные примеры: Множество G_+\subseteq G объектов, про которые известно, что они обладают целевым признаком w,
  2. отрицательные примеры: Множество G_-\subseteq G объектов, про которые известно, что они не обладают целевым признаком w,
  3. недоопределенные примеры: Множество G_{\tau}\subseteq G объектов, про которые неизвестно, обладают ли они целевым признаком или нет.

Возникают три подконтекста: K_\varepsilon: =(G_\varepsilon,M,I_\varepsilon), \varepsilon\in \{-, +, \tau\}.

В подконтекстах K_\varepsilon: =(G_\varepsilon,M,I_\varepsilon), \varepsilon\in \{-, +, \tau\} операторы Галуа и соответствующие операторы замыкания обозначаются через (\cdot)^\varepsilon, (\cdot)^{\varepsilon\varepsilon}, например, X^+, X^{++} и т.д.

Формальное содержание H\subseteq M контекста K_+ есть положительная гипотеза если H не является подмножеством содержания ни одного отрицательного примера g\in G_-: H^{++} = H, \quad \forall g\in G_-\quad H\not\subseteq g^-.

Отрицательные гипотезы определяются симметрично (c заменой + на -).

Формальное содержание H\subseteq M контекста K_- есть отрицательная гипотеза если H не является подмножеством содержания ни одного положительного примера g\in G_+:

H^{--} = H, \quad \forall g\in G_+\quad H\not\subseteq g^+.

Классификация недоопределенного примера 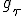g_\tau

  • Если g^{\tau}_\tau содержит в качестве подмножества положительную гипотезу и не содержит

ни одной отрицательной гипотезы, то g_\tau классифицируется положительно (предсказывается наличие целевого признака w).

  • Если g^{\tau}_\tau содержит в качестве подмножества отрицательную гипотезу и не содержит

ни одной положительной гипотезы, то g_\tau классифицируется отрицательно (предсказывается отсутствие целевого признака w).

  • Если g^{\tau}_\tau содержит в качестве подмножеств гипотезы обоих знаков или если g^{\tau}_\tau вообще не содержит в качестве подмножеств ни положительных ни отрицательных гипотез, то классификация объекта, соответственно, противоречива или недоопределенна.

Как следует из определения, для классификации достаточно иметь множество всех минимальных (относительно \subseteq, т.е. наиболее общих) гипотез.

Библиография

  • В. К. Финн, О машинно-ориентированной формализации правдоподобных рассуждений в стиле Ф. Бэкона -- Д.С. Милля \\ Семиотика и Информатика, 20(1983), 35-10
  • B. Ganter and S.O. Kuznetsov, Formalizing Hypotheses with Concepts. In: G. Mineau and B. Ganter, Eds., Proc. 8th International Conference on Conceptual Structures (ICCS 2001), Lecture Notes in Artificial Intelligence (Springer), Vol. 1867, pp. 342-356, 2000. PDF
  • S.O. Kuznetsov, Mathematical aspects of concept analysis. Journal of Mathematical Science, Vol. 80, Issue 2, pp. 1654-1698, 1996. PDF


Источник — «http://machinelearning.ru/wiki/index.php?title=%D0%94%D0%A1%D0%9C-%D0%BC%D0%B5%D1%82%D0%BE%D0%B4_%D0%B2_%D1%82%D0%B5%D1%80%D0%BC%D0%B8%D0%BD%D0%B0%D1%85_%D0%90%D0%A4%D0%9F»
Личные инструменты