Статистический анализ данных (курс лекций, К.В.Воронцов)/Чувствительность двухвыборочного критерия Стьюдента (пример)
Материал из MachineLearning.
м |
м |
||
| Строка 35: | Строка 35: | ||
Отметим, что приведённые выводы справедливы только для шума рассматриваемой структуры. | Отметим, что приведённые выводы справедливы только для шума рассматриваемой структуры. | ||
| + | |||
| + | = Ссылки = | ||
| + | * [[Статистический анализ данных (курс лекций, К.В.Воронцов)]] | ||
| + | |||
| + | [[Категория:Учебные курсы]] | ||
Текущая версия
Исследуем чувствительность классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при зашумлении выборок наблюдениями, взятыми из равномерного распределения.
— выборка длины
из смеси стандартного нормального
и равномерного
распределений с весами
и
соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит
, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).
— аналогичная выборка.
При каждом значении выборки для разных значений
генерируются независимо.
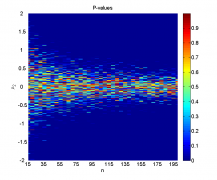
Заметим, что однократная генерация выборок даёт достаточно нестабильные результаты, не позволяя точно оценить границы области, где нулевая гипотеза отклоняется, поэтому и необходимо усреднение по большому числу экспериментов.
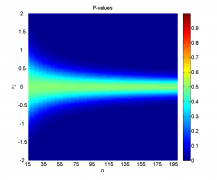
Видно, что при достаточно большой разнице между средними и большом размере выборок наличие шума не мешает уверенно отклонять гипотезу однородности. Когда, наоборот, разница между средними невелика (меньше 0.2-0.5 в зависимости от размера выборок), мощность близка к нулю, а среднее значение достигаемого уровня значимости колеблется около 0.5, что логично, так как его распределение при справедливости нулевой гипотезы равномерно на .
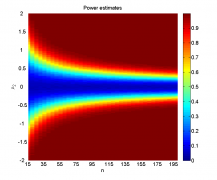
Чтобы оценить вклад зашумления выборок, оценим при всех значениях параметра мощность критерия и средний достигаемый уровень значимости на аналогичных выборках без шума и сравним результаты.
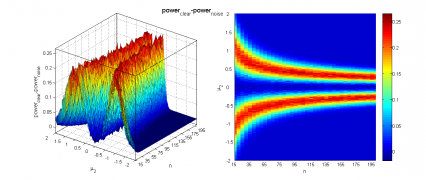
Видно, что наличие шума всё меньше влияет на работу критерия с ростом объёма выборок и разницы между их средними. Тем не менее, в некоторых областях изменения параметров потеря мощности из-за 10% зашумления может составлять до 20%, а средний достигаемый уровень значимости может быть выше на 0.1.
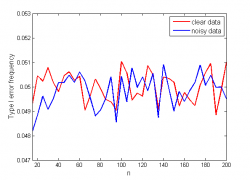
Для проверки влияния шума на корректность критерия, то есть, соответствие вероятности ошибки первого рода номинальному уровню значимости , посчитаем при различных
долю выборок, на которых при
нулевая гипотеза неверно отвергается.
Видно, что частота ошибок первого рода совершает случайные колебания около уровня 0.05, то есть, шум не влияет на корректность критерия независимо от объёма выборки.
Отметим, что приведённые выводы справедливы только для шума рассматриваемой структуры.