Обсуждение:Оценивание дискретных распределений при дополнительных ограничениях на вероятности некоторых событий (виртуальный семинар)

Материал из MachineLearning.

Версия 10:46, 29 сентября 2008

Обсуждение

• > ...Время считается дискретным...
  1. Подход, в котором плотность вначале представляется как непрерывная функция времени, мне представляется лучшим. Поскольку в таком подходе можно выбирать различное число интервалов разбиения. Интересно, что

, где seq - операция построения последовательности, а super (или ) - операция суперпозиции (сложения) многомерных дискретных элементарных исходов ( - число исходов типа k в интервале r).| ADY 11:31, 6 августа 2008 (MSD)

• > ...это приводит к появлению дополнительных ограничений типа равенств в задаче максимизации правдоподобия;...
  1. Это справедливо только в параметрическом случае и в случае, когда обратные функции (которые появятся при решении связей) будут удовлетворять некоторым условиям? | ADY 11:31, 6 августа 2008 (MSD)
  2. Максимизация правдоподобия - только один из методов получения оценок (пусть даже и с "хорошими" свойствами).
• > ...выборка может быть «немного» неоднородной;...
  1. Если вводить веса (через ядро), то, такое впечатление, это эквивалентно тому, что мы делаем выборку однородной, но во всех функционалах учитываем веса. Если решение пойдет по этому пути, тогда можно подумать на тему введения весов для каждого элемента эмпирических данных? | ADY 11:31, 6 августа 2008 (MSD)

• Проблема: Можно ли использовать на первом этапе, в качестве оценок эмпирические данные (частоты) (без поиск параметрических или основанных на ядрах оценок)?
• Обсуждение: скорей всего да, то нужно накладывать дополнительные условия (типа , начиная с некоторого n, и , при некоторых условиях на заданные функционалы), трансформировать плотности соответствующим образом и проверять качество этих допущений.

Дальнейшее обобщение задачи. Другие проблемы

• Если ввести гипотезу о том, что семейство распределений зависит от величин связи , и построить решетку для параметров , , то соседние распределения (как по , так и по ) будут удовлетворять некоторым условиям. Например, известны условия монотонности для вероятностей некоторых исходов. Следовательно, следует потребовать выполнения этих условий для оценок вероятностей. Кроме того, для каждого распределения известны некоторые разумные ("внутренние") условия на вероятности, выполнение которых тоже целесообразно потребовать для оценок на вероятности.

• При восстановлении плотности (для выбранного числа интервалов) в качестве функционала качества хотелось бы принять описанный функционал:

. Возможно, этот функционал можно как-то упростить.

• Нужны критерии для сравнения различных плотностей и схема тестирования.
• Хотелось бы построить доверительные интервалы для оценок плотностей. При построении доверительных интервалов можно отказаться от квадратичного функционала при оценки вероятностей сверху использовать минимизацию:

, а при оценки снизу минимизировать: , для (где - мин. допустимая оценка на вероятность).

• В задаче, оценки на вероятность всегда имеют некоторую естественную ошибку (обозначим ее ), не связанную с величиной выборки. Ее природа в невозможности точно отнести эмпирические данные к одному из семейству распределений. Поэтому, нет смысла строить бесконечно точные оценки (точные оценки в пределе): достаточно строить оценки, точноcть которых быстро стремиться к при росте числа элементов выборки. В частной постановке задачи .

| ADY 12:13, 6 августа 2008 (MSD)

• Условие задачи можно расширить, учитывая дополнительное условие, что со всеми эмпирическими данными (то есть данными о реализациях изучаемого случайного процесса) идут некоторые оценки значений связей . Следовательно, выборки и выделение различных распределений, можно генерировать на основе этих данных о связях (и, соответственно, появляется новая задача - разбиение всех эмпирических данных на классы, согласно эмпирических данным и оценкам на значения ). | ADY 16:18, 11 августа 2008 (MSD)
• Стоит также задача, как наиболее оптимально, выделить маргинальные частотные плотности и из совместной эмпирической плотности . Допустимость независимого выделения этих плотностей, например, как , требует дополнительного анализа, поскольку в этом случае , хотя известно, что - вполне нормальная оценка для . | ADY 16:13, 20 августа 2008 (MSD)

Особенности восстановления плотности через максимизацию правдоподобия (для интегральных исходов)

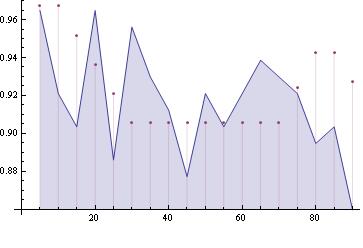
• Есть впечатление, что восстановления плотности через максимизацию правдоподобия для интегральных исходов имеет некоторые особенности. Например, в следующей картинке видно, что оценка "угадывает" наличие "горба", но "не угадывает" локальные свойства горба (что, в самом деле, вполне логично). Видно, что оценкой плотности для последнего интервала пользоваться скорей всего нельзя.
• Синим закрашена область - плотность события (где - число событий в i-ом интервале). Точками показана та же самая плотность, параметры которой оценены по максимуму правдоподобия.

| ADY 11:44, 8 августа 2008 (MSD)

Особенности восстановления многомерной совместной плотности распределения на основе принципа максимального правдоподобия

Стоит задача найти оценку плотности распределения событий в интервалах (в каждом из которых может произойти 0 или 1 событие) таким образом, чтобы все частные плотности, то есть плотности, которые получаются из общей при условии, что события в начальных интервалах уже реализовались, тоже, так или иначе, удовлетворяли принципу максимального правдоподобия. Общая плотность имеет вид: . Где - функция распределения событий в k-ом интервале. . Для конкретной задачи можно запостулировать следующий параметрический вид функций распределений в интервале:

• , для
• , для
• , для

Можно предложить следующий способ оценки совместной плотности распределения событий, в соответствии с принципом максимального правдоподобия.

• Отбросив события для всех N-1 интервалов, из принципа максимального правдоподобия для последнего интервала получаем, что , где - эмпирическая частота выпадения нулевого числа событий в последнем интервале (индекс вверху показывает, что отсчет идет справа налево (поэтому "-"), и указывает номер интервала в текущем способе отсчета).
• Из параметрического вида распределений в интервалах имеем: . Рассматривая плотность для двух последних интервалов, можно построить следующую функцию распределения для этих интервалов:

Поскольку оценку величены p0(N) мы считаем известной, а , то по принципу максимального правдоподобия можно найти оценку на величену параметра , где - значения эмпирически частот выпадения событий в двух последних интервалах.

• Проблема 1: величену можно оценить в точности аналогичным образом взяв любое количество от 2 до последних интервалов.
• Оценив из частот для последних 1 и K-интервалов качество этой оценки для построения ф.р.в. для всех остальных интервалов (для ) становится не ясным?
• Замечание: В качестве начальной известной оценки для можно использовать оценку для частоты в любом интервале (-K).
• Какую оценку для в итоге использовать?
• Как усреднять все возможные оценки? Если оценок будет слишком много, то как усреднять по классу всех возможных оценок?
• Увеличивая количество интервалов K так, что , в игру вступает параметр . Вопрос, какую оценку для можно использовать при построении совместной функции распределения для последующей оценки, максимизацией правдоподобия, для .
• Как наилучшим образом использовать информацию о частотах, из которых можно построить оценку для одного и тоже же параметра?
• Используя оценку такого типа, параметр p0 (из формул для распр. вер. в интервалах) теряет свою необходимость. Почему эта степень свободы оказалась фиктивной?
• Функция распределения при рассмотрении > 4 интервалов не должна усложняться слишком сильно (поскольку для любого K).
• Можно ли понять качество оценок в смысле используемого в задаче функционала качества. Возможно, использование функционала качества такого типа поможет устранить неоднозначность построения оценок по принципу максимального правдоподобия для выбранного параметрического вида модели.
• Можно ли построить содержательные критерии для выбора неявных параметров и . Возможно при построении таких критериев окажется полезным принцип минимума .
• Замечание: пишут, что по ML плотность обычно не оценивают (см. [1], стр.6).

Полезные статьи

1. Изображение:Multi-dim density estimation.pdf
2. Изображение:MDL Histogram density estimation.pdf