Использование технологий NVIDIA для решения задач глубокого обучения

Материал из MachineLearning.

Версия 19:39, 20 апреля 2015

Ниже приведен обзор методов построения сетей глубокого обучения на графических акселераторах. Решаются задачи машинного обучения: распознавания образов, речи, классификация сигналов. Для решения задач используются программные пакеты Torch, Theano, Caffe, cuDNN, предназначенные для работы с графическими ускорителями NVIDIA. Сравнивается работа ускорителей, Tesla X и [наш], на серверах mvr.jmlda.org и Amazon S3.

Matlab Parallel Computing Toolbox

Статья наполняется. Категория: Инструменты и технологии. --Strijov 15:57, 20 апреля 2015 (MSD)

Запуск функций CUDA в Matlab

Parallel Computing Toolbox в Matlab предоставляет фреймворк для вычислений на GPU.

Для того, чтобы разместить структуру данных Matlab (массив или матрицу численного типа) в памяти GPU, используется функция gpuArray(). Вызов этой функции создает объект Matlab в памяти GPU:

N = 6;
M = magic(N);
G = gpuArray(M);

Для того, чтобы вернуть массив из памяти GPU в Matlab workspace, используется функция gather():

G = gpuArray(ones(100,'uint32'));
D = gather(G);

Для работы со структурами данных gpuArray в Matlab предусмотрено несколько вариантов. Одним из вариантов (наиболее низкоуровневом) является запуск предварительно скомпилированной функции ядра CUDA с расширением .cu. Для запуска функции в Matlab необходимо создать объект CUDAKernel и выполнить следующую последовательность действий:

1. Скомпилировать файл с расширением .ptx для функции ядра myfun.cu с помощью, например, компилятора nvcc в NVIDIA CUDA Toolkit:

nvcc -ptx myfun.cu

2. Создать объект CUDAKernel с аргументами .ptx, .cu:

k = parallel.gpu.CUDAKernel('myfun.ptx','myfun.cu');

3. Присвоить объекту CUDAKernel параметры, необходимые для выполнения на GPU:

k.GridSize = [8 1];
k.ThreadBlockSize = [16 1];

4. Вызвать функцию feval для выполнения CUDAKernel:

g1 = gpuArray(in1); % Input gpuArray.
g2 = gpuArray(in2); % Input gpuArray.
 
result = feval(k,g1,g2);

Функции Matlab с реализацией под GpuArray

Рис.1. Обращение матрицы.

Рис.2. Умножение матриц.

Рис.3. Сингулярное разложение матрицы.

Помимо запуска функций, написанных на CUDA, в Matlab реализована перегрузка некоторых встроенных функций, принимающих в качестве аргумента массив в памяти GPU gpuArray. Их полный список приведен в [1]. В частности, для работы с gpuArray реализованы следующие функции, выполняющие простейшие алгебраические и статистические операции:

conv, eig, fft, filter, median, mean, rand, std, svd, inv, pinv

Реализация этих функций позволяет работать напрямую с массивами GpuArray:

Ga = rand(1000,'single','gpuArray');
Gfft = fft(Ga);
Gb = (real(Gfft) + Ga) * 6;
G = gather(Gb);

Однако список этих функций и, как следствие, его применимость в реальных задачах, является крайне ограниченным.

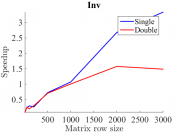
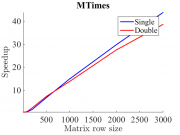
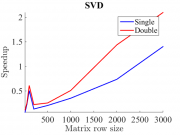
На рис. 1-3 показаны примеры тестирования некоторых встроенных Matlab-функций на GPU. Тестирование производилось на видеокарте GeForce GTX 660 Ti. Приведены примеры тестирования функций обращения матрицы, умножения двух матриц и сингулярного разложения матрицы. По оси абсцисс каждого графика отложен строковый размер матрицы, по оси ординат - скорость выполнения по сравнению с GPU. Синей линией проиллюстрированы результаты для типа данных single, красной -- для типа данных double. Видно, что для алгоритма с простой параллелизацией (MTimes) ускорение достигает порядка 40X на данных большого объема. В то же время для алгоритмов с плохой паралеллизацией (inv, svd) ускорение достигает лишь порядка 1X-2X. Кроме того, замечено, что для типа данных single ускорение в среднем больше.

Реализация arrayFun для массива в памяти GPU

Помимо встроенных функций алгебраических вычислений для работы с массивами gpuArray в Matlab реализовано выполнение функций arrayfun и bsxfun. Выполнение этих функций аналогично выполнению соответствующих функций arrayfun и bsxfun, но происходит с использованием памяти GPU. Эта возможность позволяет вычислять на GPU функции Matlab, написанные разработчиком для поэлементных операций над массивом или матрицей.

В качестве примера продемонстрируем вычисление матрицы парных евклидовых расстояний между набором точек. Размерность евклидова пространства во всех случаях .

Функция, поступающая в качестве первого аргумента для arrayfun - поэлементная функция расстояния между двумя координатами точек:

distfun = @(a, b) ((a - b) ^ 2);

Рис.4. Вычисление парных расстояний с помощью arrayfun.

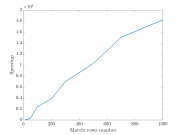
Результат выполнения функции arrayfun на CPU и GPU показан на рис. 4. Видно, что достигаемое ускорение для "наивного" вычисления расстояний составляет десятки тысяч.

Несмотря на хорошие результаты исследования, существует ряд ограничений на поэлементную функцию при работе с arrayfun на GPU, что делает применение этой функциональности достаточно узким. Наиболее полный список этих ограничений приведен в [2]. Ниже приведен список основных ограничений.

1. Внутри поэлементной функции запрещено использовать операции изменения формы входного или выходного массивов (cat, reshape etc.). Это связано с тем, что массивы размещаются в памяти GPU.
2. Функции arrayfun и bsxfun не могут обращаться к переменным вне области видимости, а также к переменным, которые были созданы до начала вычисления функции на GPU. Это ограничение делает невозможным вычисление функции расстояния произвольного вида. Возможным оказывается считать только те расстояния, которые могут быть вычислены независимо по координатам (например, евклидово).
3. Поэлементные анонимные функции не имеют доступа к области видимости их родительского окружения.