Использование технологий NVIDIA для решения задач глубокого обучения

Материал из MachineLearning.

Версия 15:19, 8 июля 2015

Ниже приведен обзор методов построения сетей глубокого обучения на графических ускорителях. Решаются задачи машинного обучения: распознавания образов, речи, классификация сигналов. Для решения задач используются программные пакеты Torch, Theano, Caffe, cuDNN, предназначенные для работы с графическими ускорителями NVIDIA. Сравнивается работа ускорителей, Tesla X и [наш], на серверах mvr.jmlda.org и Amazon S3.

Глубокое обучение – быстро развивающийся сегмент области знания, связанной с искусственным интеллектом, - является катализатором развития самых разных отраслей, начиная от медицины и фармакологии и заканчивая автопилотируемыми автомобилями. Глубокое обучение (глубокое структурное обучение, или иерархическое обучение) -- это область машинного обучения, заключающаяся в построении нелинейной модели распознавания, каждый элемент которой описывает соответствующий уровень признакового агрегирования данных.

На конференции "GPU Technology Conference" [1] в 2015 г. генеральным директором NVIDIA Дженсоном Хуангом было представлено три новые технологии, которые используются для развития области глубокого обучения: TITAN X, DIGITS и DIGITS DevBox.

NVIDIA GeForce GTX TITAN X

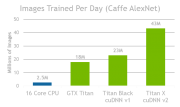
TITAN X [2] – графический процессор для быстрого обучения глубоких нейронных сетей. Построенный на графической архитектуре NVIDIA Maxwell, TITAN X обладает вдвое большей производительностью и энергоэффективностью по сравнению с предшественником. TITAN X – это 12ГБ памяти и 3072 ядра, которые обеспечивают 7 терафлопс в вычислениях одинарной точности. Благодаря производительности и полосе пропускания памяти 336.5 ГБ/с, ускоритель рекомендуется использовать для построения сетей глубокого обучения с числом параметров до сотен миллионов. В частности, для обучения сети AlexNet [3] с помощью набора из 1.2 миллиона изображений ImageNet TITAN X понадобилось менее трех дней, тогда как 16-ядерный CPU справляется с этой задачей за 40 дней.

cuDNN

Сравнение времени обучения нейронной сети Ceffe AlexNet на 1) CPU, 2) Titan GPU, 3) cuDNN v1, 4) cuDnn v2.

cuDNN [4] -- это ускоренная на GPU библиотека примитивов для сверточных нейронных сетей. cuDNN имеет свободное распространение и доступна зарегистрированным на NVIDIA разработчикам [5]. Примитивы библиотеки cuDNN используются в высокоуровневых фреймворках Caffe [6], Theano [7] и Torch [8].

Библиотека cuDNN предоставляет следующую функциональность:

• Процедуры forward-backward оптимизации.
• Операции над тензорами и их использование в алгоритмах построения нейронных сетей.
• Функции активации нейронной сети (кусочно-линейная, сигмоидная, функция гиперболического тангенса).
• Простое интегрирование в любую конфигурацию нейронной сети.

DIGITS Deep Learning GPU Training System

Рис.1. Консоль DIGITS

Рис. 2: Инициализация данных

Рис. 3: Конфигурирование модели

Рис. 4: Результаты обучения

DIGITS [9] – программное обеспечение с открытым кодом [10], предназначенное для выполнения исследовательских работ по построению и конфигурации глубоких нейронных сетей. Интуитивно понятный пользовательский интерфейс и возможности управления DIGITS обеспечивают подготовку обучающих наборов данных локально и из сети. Типичным примером модели, оптимизируемой DIGITS, является комбинация сверточных нейронных сетей (CNN) для задачи классификации изображений. DIGITS использует примитивы библиотеки cuDNN.

Преимущества DIGITS

Основным преимуществом системы DIGITS является пользовательский интерфейс, взаимодействующий с пользователем через Web-приложение и ускоряющий процедуру инициализации необходимой модели [11].

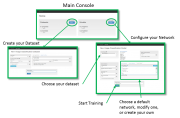
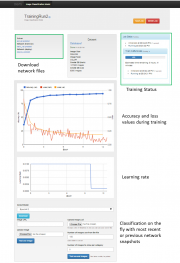
Пример работы с DIGITS показан на рис. 1. Первый блок является главным, в нем осуществляется инициализация данных и подготовка моделей к оптимизации. По мере настройки параметров, пользователь может вносить изменения в структуру модели и выбирать модели оптимальной точности распознавания.

Кроме того, система DIGITS позволяет визуализировать нейронные сети и сохранять ранее полученные результаты и модели для сравнения с новыми. Реализованное Web-приложение позволяет группе исследователей обмениваться данными, моделями и результатами.

Использование DIGITS

Для запуска DIGITS необходимо выполнить следующие действия.

1. Зарегистрироваться на NVIDIA в качестве разработчика [12] и скачать установочный файл [13].
2. После установки необходимо запустить локально Web-приложение:

   python digits-devserver

3. После запуска приложения Web-интерфейс DIGITS будет доступен в браузере по локальному адресу http://localhost:5000.
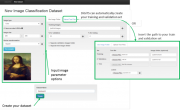
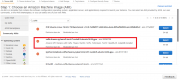
4. Инициализировать базу данных изображений, как показано на рис. 2. Это можно сделать двумя способами: 1) прописать путь к директории с изображениями и 2) загрузить изображения через Web-форму.
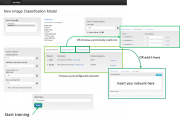
5. Инициализировать модель распознавания и параметры ее обучения. Для этого есть три способа: использовать одну из двух имеющихся конфигураций (LeNet и AlexNet), использовать предыдущую конфигурацию, задать конфигурацию вручную.
6. Запустить процедуру обучения, получить результат в виде графиков функции ошибки и оптимальных параметров.

DIGITS DevBox

DIGITS DevBox [14] – специализированная рабочая станция для работы с задачами глубокого обучения, построенная на базе четырех TITAN X GPU, поставляемое с предустановленной системой обучения DIGITS. Система DIGITS DevBox является ядром комплексной платформы для ускорения исследований глубокого обучения. DevBox состоит из четырех карт GPU TITAN X, памяти и интерфейсов. Система поставляется с предустановленным программным обеспечением, которое необходимо ученым и исследователей для создания собственных глубоких нейронных сетей. В список приложений входят пакет программ DIGITS, самые популярные платформы глубокого обучения Caffe, Theano и Torch, а также cuDNN 2.0 – GPU-ускоренная библиотека для задач глубокого обучения от NVIDIA [15]. Первые результаты многопроцессорного обучения показывают, что DIGITS DevBox обеспечивает производительность почти в четыре раза выше по сравнению с одним TITAN X в тестах глубокого обучения. С помощью DIGITS DevBox обучить сеть AlexNet можно всего за 13 часов, тогда как обычному ПК на базе самого быстрого GPU потребовалось бы более двух суток, а системе на базе CPU - больше месяца.

Система DIGITS DevBox состоит из следующих компонентов.

• Четыре TITAN X GPU, обеспечивающие 7 тетрафлопс в ординарной точности, 12 Гб памяти и 336.5 Гб/с полосы пропускания памяти. В комплект DIGITS DevBox входят до четырех GPUs, до 64 GB DDR4, материнская плата ASUS X99 (8 PCIe slots) + Core i7, 2 x 48 port gen3 PCIe (PEX8748) + CPU for PCIe, накопитель, до 3x3 TB RAID 5 + M2 SATA + SSD, блок питания 1500W, операционная система Ubuntu 14.04, драйвера, NVIDIA® CUDA® Toolkit 7.0.
• Программное обеспечение NVIDIA DIGITS, предоставляющее интерфейсы для обучения и визуализации нейронных сетей для классификации изображений.
• Система Ubuntu 14.04 с предустановленными Caffe, Torch, Theano, BIDMach, cuDNN v2, and CUDA 7.0.

С чего начать

1. Посмотреть вебинар по сверточным нейронным сетям [16] и Caffe для глубокого обучения [17].
2. Установить фреймворк по выбору: Caffe, Torch или Theano.
3. Загрузить и установить cuDNN [18], ускоренную на GPU библиотеку NVIDIA, содержащую примитивы для глубоких нейронных сетей.

Первая программа на CUDA

Чтобы написать первую программу на CUDA, надо установить:

1. Microsoft Visual Studio (на MVR стоит версия Professional 2012),
2. CUDA SDK (на MVR стоит версия 7.0) [19].

После установки SDK стоит посмотреть полезные примеры от NVIDIA, которые по умолчанию распаковываются в C:\ProgramData\NVIDIA Corporation\CUDA Samples\v7.0. Кроме того, появится возможность компилировать .cu файлы командой nvcc из командной строки, например,

nvcc -ptx myfun.cu

Это нужно, например, для того, чтобы использовать CudaKernel в Matlab для запуска своих CUDA-функций, см. [20].

Руководство по установке Caffe на Windows: [21]. Highlights: нужно поставить и прописать зависимости для OpenCV, Boost, OpenBLAS, GFlags, GLog, ProtoBuf, LevelDB, HDF5, LMDB. Кроме того, для облегчения процесса сборки понадобится установить CMake.

Руководство по установке Theano на Windows: [22].

Работа с Theano на Amazon Web Services

При отсутствии устройства GPU на локальной машине можно воспользоваться платным удаленным фреймворком, например, Amazon Web Services [23].

Подробные инструкции по инициализации удаленных вычислений на GPU, а также по удаленному использованию библиотек глубокого обучения можно прочитать в [24], [25], [26].

Список библиотек высокого уровня для работы с GPU

• Caffe: Framework for convolutional neural network algorithms
• cuda-convnet: High performance C++/CUDA implementation of convolutional neural networks
• Theano: Python library to define, optimize, and evaluate mathematical expressions
• Torch7: Scientific computing framework for machine learning algorithms
• cuBLAS: GPU-accelerated version of the complete standard BLAS library
• MATLAB: Easy-to-use HPC language integrating computation, visualization, and programming cxxnet: Neural network toolkit
• Отчет о производительности CUDA 6.5 и библиотек

Matlab Parallel Computing Toolbox

Запуск функций CUDA в Matlab

Parallel Computing Toolbox в Matlab предоставляет фреймворк для вычислений на GPU.

Для того, чтобы разместить структуру данных Matlab (массив или матрицу численного типа) в памяти GPU, используется функция gpuArray(). Вызов этой функции создает объект Matlab в памяти GPU:

N = 6;
M = magic(N);
G = gpuArray(M);

Для того, чтобы вернуть массив из памяти GPU в Matlab workspace, используется функция gather():

G = gpuArray(ones(100,'uint32'));
D = gather(G);

Для работы со структурами данных gpuArray в Matlab предусмотрено несколько вариантов. Одним из вариантов (наиболее низкоуровневом) является запуск предварительно скомпилированной функции ядра CUDA с расширением .cu. Для запуска функции в Matlab необходимо создать объект CUDAKernel и выполнить следующую последовательность действий:

1. Скомпилировать файл с расширением .ptx для функции ядра myfun.cu с помощью, например, компилятора nvcc в NVIDIA CUDA Toolkit:

nvcc -ptx myfun.cu

2. Создать объект CUDAKernel с аргументами .ptx, .cu:

k = parallel.gpu.CUDAKernel('myfun.ptx','myfun.cu');

3. Присвоить объекту CUDAKernel параметры, необходимые для выполнения на GPU:

k.GridSize = [8 1];
k.ThreadBlockSize = [16 1];

4. Вызвать функцию feval для выполнения CUDAKernel:

g1 = gpuArray(in1); % Input gpuArray.
g2 = gpuArray(in2); % Input gpuArray.
 
result = feval(k,g1,g2);

Функции Matlab с реализацией под GpuArray

Рис.1. Обращение матрицы.

Рис.2. Умножение матриц.

Рис.3. Сингулярное разложение матрицы.

Помимо запуска функций, написанных на CUDA, в Matlab реализована перегрузка некоторых встроенных функций, принимающих в качестве аргумента массив в памяти GPU gpuArray. Их полный список приведен в [27]. В частности, для работы с gpuArray реализованы следующие функции, выполняющие простейшие алгебраические и статистические операции:

conv, eig, fft, filter, median, mean, rand, std, svd, inv, pinv

Реализация этих функций позволяет работать напрямую с массивами GpuArray:

Ga = rand(1000,'single','gpuArray');
Gfft = fft(Ga);
Gb = (real(Gfft) + Ga) * 6;
G = gather(Gb);

Однако список этих функций и, как следствие, его применимость в реальных задачах, является крайне ограниченным.

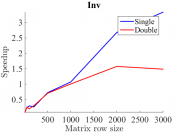
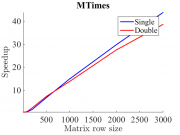
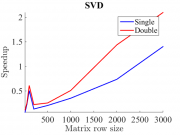
На рис. 1-3 показаны примеры тестирования некоторых встроенных Matlab-функций на GPU. Тестирование производилось на видеокарте GeForce GTX 660 Ti. Приведены примеры тестирования функций обращения матрицы, умножения двух матриц и сингулярного разложения матрицы. По оси абсцисс каждого графика отложен строковый размер матрицы, по оси ординат - скорость выполнения по сравнению с GPU. Синей линией проиллюстрированы результаты для типа данных single, красной -- для типа данных double. Видно, что для алгоритма с простой параллелизацией (MTimes) ускорение достигает порядка 40X на данных большого объема. В то же время для алгоритмов с плохой паралеллизацией (inv, svd) ускорение достигает лишь порядка 1X-2X. Кроме того, замечено, что для типа данных single ускорение в среднем больше.

Реализация arrayFun для массива в памяти GPU

Помимо встроенных функций алгебраических вычислений для работы с массивами gpuArray в Matlab реализовано выполнение функций arrayfun и bsxfun. Выполнение этих функций аналогично выполнению соответствующих функций arrayfun и bsxfun, но происходит с использованием памяти GPU. Эта возможность позволяет вычислять на GPU функции Matlab, написанные разработчиком для поэлементных операций над массивом или матрицей.

В качестве примера продемонстрируем вычисление матрицы парных евклидовых расстояний между набором точек. Размерность евклидова пространства во всех случаях .

Функция, поступающая в качестве первого аргумента для arrayfun - поэлементная функция расстояния между двумя координатами точек:

distfun = @(a, b) ((a - b) ^ 2);

Рис.4. Вычисление парных расстояний с помощью arrayfun.

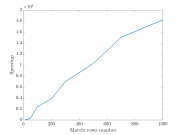
Результат выполнения функции arrayfun на CPU и GPU показан на рис. 4. Видно, что достигаемое ускорение для "наивного" вычисления расстояний составляет десятки тысяч.

Несмотря на хорошие результаты исследования, существует ряд ограничений на поэлементную функцию при работе с arrayfun на GPU, что делает применение этой функциональности достаточно узким. Наиболее полный список этих ограничений приведен в [28]. Ниже приведен список основных ограничений.

1. Внутри поэлементной функции запрещено использовать операции изменения формы входного или выходного массивов (cat, reshape etc.). Это связано с тем, что массивы размещаются в памяти GPU.
2. Функции arrayfun и bsxfun не могут обращаться к переменным вне области видимости, а также к переменным, которые были созданы до начала вычисления функции на GPU. Это ограничение делает невозможным вычисление функции расстояния произвольного вида. Возможным оказывается считать только те расстояния, которые могут быть вычислены независимо по координатам (например, евклидово).
3. Поэлементные анонимные функции не имеют доступа к области видимости их родительского окружения.