Участник:Gukov/Песочница
Материал из MachineLearning.
(→Числовой пример) |
(→Числовой пример) |
||
| Строка 95: | Строка 95: | ||
:<tex>\int^{5}_{1} \ln x\, dx = x \ln x - x |_1^{5} = 5\ln 5 - 4</tex> | :<tex>\int^{5}_{1} \ln x\, dx = x \ln x - x |_1^{5} = 5\ln 5 - 4</tex> | ||
| + | [[Изображение:Result.png|thumb|300px]] | ||
В нижеследующей таблице представлены результаты работы программы: | В нижеследующей таблице представлены результаты работы программы: | ||
{|border = '1' | {|border = '1' | ||
| Строка 152: | Строка 153: | ||
| | | | ||
|} | |} | ||
| + | |||
| + | Здесь <tex>r</tex> - число отрезков, на которые разбивается сегмент <tex>[1, 5]</tex>. | ||
| + | |||
| + | На иллюстрации черная сплошная линия - вычисление значения интеграла по исходной формуле, зеленая пунктирная - по экстраполированной 1 раз формуле, красная пунктирная - по экстраполированной 3 раза формуле. | ||
| + | |||
| + | Как мы видим, разница между экстраполированными и неэкстраполированными результатами значительна. | ||
== Рекомендации программисту == | == Рекомендации программисту == | ||
Версия 22:07, 19 октября 2008
Содержание |
Введение
Постановка математической задачи
Задача численного интегрирования состоит в приближенном нахождении значения интеграла
где
- заданная и интегрируемая на
функция. В качестве приближенного значения рассматривается число
где - числовые коэффициенты и
- точки отрезка
,
.
Приближенное равенство
называется квадратурной формулой, а сумма вида (2) - квадартурной суммой. Точки называются узлами квадратурной формулы.
Разность
называется погрешностью квадратурной формулы. Погрешность зависит как от расположения узлов, так и от выбора коэффициентов.
Изложение метода
Общие сведения
Предположим, что для вычисления интеграла (1) отрезок разбит на
равных отрезков длины
и на каждом частичном отрезке применяется одна и та жа квадратурная формула. Тогда исходный интеграл
заменяется некоторой квадратурной суммой
, причем возникающая погрешность зависит от шага сетки
.
Для некоторых квадратурных формул удается получить разложение погрешности
по степеням
. Предположим,
что для данной квадратурной суммы
существует разложение:
,
где и коэффициенты
не зависят от
.
При этом величины
предполагаются известными.
Теперь предположим:
Чтобы избавиться от степени , составляющей ошибку (ибо среди всех слагаемых, составляющих ошибку, слагамое при
является наибольшим) вычислим величину
. Имеем:
Отсюда
то есть имеем более точное приближение к интегралу .
Таким образом, рекуррентную формулу можно записать в виде:
Заметим, что - величина, на которую мы делим размер шага при каждом новом вычислении
. Разумно положить
, т.к. большие значения
могут вызвать резкое увеличение количества вычислений.
Для наглядности представим процесс экстраполирования следующей таблицей:
О сходимости
Числовой пример
Найдем с помощью квадратурной формулы трапеций приближенное значение интеграла, применив экстраполяцию Ричардсона (данный метод называется методом Ромберга):
В нижеследующей таблице представлены результаты работы программы:
| r | Исходная формула | 1 раз | 3 раза |
| 2 | 1.609438 | 2.925492 | 3.92582 |
| 4 | 2.256648 | 3.506035 | 3.987405 |
| 8 | 3.278646 | 3.778845 | 4.017368 |
| 16 | 3.653497 | 3.913012 | 4.032286 |
| 32 | 3.848134 | 3.980123 | 4.039738 |
| 64 | 3.947125 | 4.013659 | 4.043464 |
| 128 | 3.997025 | 4.030424 | 4.045327 |
| 256 | 4.022075 | 4.03880706 | |
| 512 | 4.034624 | 4.042998 | |
| 1024 | 4.040904 |
Здесь - число отрезков, на которые разбивается сегмент
.
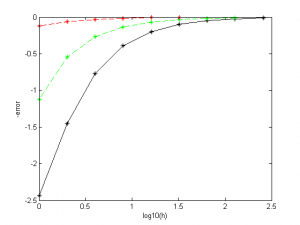
На иллюстрации черная сплошная линия - вычисление значения интеграла по исходной формуле, зеленая пунктирная - по экстраполированной 1 раз формуле, красная пунктирная - по экстраполированной 3 раза формуле.
Как мы видим, разница между экстраполированными и неэкстраполированными результатами значительна.
Рекомендации программисту
Заключение
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
- Fundamental Methods of Numerical Extrapolation With Applications, mit.edu