м |
м |
| Строка 1: |
Строка 1: |
| - | Ниже под обозначением <tex>X^n, \;\; X \sim p\cdot F_1+ \left(1-p\right)\cdot F_2</tex> понимается выборка объёма <tex>n</tex> из смеси распределений <tex>F_1</tex> и <tex>F_2</tex> с весами <tex>p</tex> и <tex>1-p</tex> соответственно (при генерации каждой выборки используется случайный датчик — если его значение не превосходит <tex>p</tex>, то добавляем в выборку элемент, взятый из <tex>F_1</tex>, иначе — элемент, взятый из <tex>F_2</tex>).
| + | ===Биоразлагаемость молекул=== |
| | + | 1055 химических молекул описаны с помощью 41 признака (число атомов кислорода, нитратных групп, донорных связей с водородом, потенциал ионизации и т.д.); 355 из них биоразложимы. (biodeg.xlsx) |
| | + | :: : какие свойства молекул влияют на их биоразлагаемость? |
| | | | |
| - | = Анализ поведения схожих критериев = | + | ===Сейсмическая опасность в шахтах=== |
| - | Требуется исследовать поведение указанной пары статистических критериев, подходящих для решения одной и той же задачи, сравнить мощность и достигаемые уровни значимости и сделать выводы о границах применимости критериев. Необходимо для каждого из критериев построить графики зависимости достигаемых уровней значимости и оценок мощностей от параметров, и показать, в каких областях изменения параметров предпочтительнее использовать тот или иной критерий. Для получения более гладких графиков рекомендуется применять оба критерия к одним и тем же выборкам, а не генерировать их отдельно для каждого.
| + | Собраны данные мониторинга сейсмической активности в польских угольных шахтах столбовой системы разработки. При сейсмической опасности существует серьёзный риск обрушения; в этом случае необходимо отозвать рабочих или использовать направленные взрывы для нейтрализации напряжения породы. Для каждого измерения известен бинарный индикатор сейсмической опасности — наличия в следующую восьмичасовую смену сейсмических толчков с энегрией выше <tex>10^4</tex> Джоулей. (seismic.xlsx) |
| | + | :: : построить модель сейсмической опасности, дать интерпретацию вклада показателей сейсмической активности. |
| | | | |
| - | * <tex> X_1^{n_1}, \;\; X_1 \sim F_1,</tex> <br> <tex> X_2^{n_2}, \;\; X_2 \sim F_2; <tex> <br> <tex> H_0 \,:\, F_1=F_2, </tex><br> <tex>H_1\,:\; H_0 </tex> неверна. <br>
| + | ===Преступность и демографические характеристики=== |
| - | ::: <tex>F_1 = U\left[0,1\right], \;\; F_2 = U\left[a,a+1\right]</tex> — непрерывные равномерные распределения; <tex>a = 0\,:\,0.02\,:\,3, \;\; n_1=n_2=5\,:\,1\,:\,70.</tex> Сравнить критерии Смирнова и Крамера-фон Мизеса. <!--- брать a до 2--->
| + | Данные собраны из переписи населения США 1990 года, отчёта ФБР о преступности за 1995 год и опроса сотрудников полиции LEMAS за 1990 год. По 2215 округам собрана статистика преступлений и 125 демографических показателей. (crimes.xlsx) |
| - | ::: <tex>F_1 = N(0,1), \;\; F_2 = N(\mu,\sigma^2), \;\; \mu = 0\,:\,0.01\,:\,2, \;\; \sigma=0.5\,:\,0.01\,:\,2, \;\; n_1=n_2=30.</tex> Сравнить критерии Смирнова и Крамера-фон Мизеса.
| + | :: : построить функцию, оценивающую абсолютное число автомобильных краж по демографическим показателям, дать интерпретацию коэффициентов модели. |
| - | ::: <tex>F_1 = N(0,1), \;\; F_2 = p\cdot N(0,1)+ \left(1-p\right)\cdot U\left[-\sqrt{3}, \sqrt{3}\right]; \;\; p=0\,:\,0.01\,:\,1, \;\; n_1=n_2=5\,:\,1\,:\,70.</tex> Сравнить критерии Смирнова и его бутстреп-версию (функция ks.boot в пакете Matching). | + | |
| | | | |
| - | * <tex>X^n, \;\; X \sim p\cdot N(0,1)+ \left(1-p\right)\cdot F;</tex> <br> <tex> H_0\,:\; X \sim N,</tex> <br> <tex>H_1\,:\; H_0 </tex> неверна.
| + | ===Токсичность рыб=== |
| - | ::: <tex>F = C\left(0,1\right)</tex>— стандартное распределение Коши; <tex>n=20\,:\,1\,:\,100, \;\; p=0\,:\,0.01\,:\,1.</tex> Сравнить критерии Шапиро-Уилка и хи-квадрат Пирсона.
| + | Полихлорированные дифенилы — органические соединения, активно использовавшиеся в промышленности до 1970 годов, когда была показана их токсичность. Накопление ПХБ в организме приводит к подавлению иммунитета, провоцирует развитие рака, поражений печени, почек, нервной системы, кожи, способствуют развитию детской патологии. Из-за накопления ПХБ в озёрах США некоторые виды рыб в некоторых областях запрещены к употреблению в пищу. Для своевременного обновления таких запретов необходимо периодически проводить мониторинг ПХБ. К сожалению, существует 209 различных разновидностей ПХБ, концентрация каждой из которых измеряется отдельным тестом. |
| - | ::: <tex>F = U[-a,a]</tex>— непрерывное равномерное распределение; <tex>a=0.1\,:\,0.05\,:\,5, \;\; n=50, \;\; p=0\,:\,0.01\,:\,1.</tex> Сравнить критерии Харке-Бера и Андерсона-Дарлинга.
| + | Для 69 видов рыбы известны концентрации семи соединений ПХБ (в миллионных долях), а также суммарная концентрация всех разновидностей ПХБ, их токсическая эквивалентность (TEQ) и суммарная токсическая эквивалентность образца, определяемая также вкладом диоксинов и фуранов. (pcb.txt) |
| - | ::: <tex>F = St(2)</tex> — распределение Стьюдента с двумя степенями свободы; <tex>n=10\,:\,1\,:\,70, \;\; p=0\,:\,0.01\,:\,1.</tex> Сравнить критерии Харке-Бера и хи-квадрат Пирсона.
| + | :: : насколько точно токсичность рыбы можно предсказывать по концентрации только нескольких ПХБ? Концентрации какого минимального количества соединений ПХБ нужно измерить, чтобы достаточно точно предсказать суммарную токсичность, или хотя бы токсичность только совокупности ПХБ? |
| - | | + | |
| - | * <tex>X^n, \;\; X\sim Ber(p); </tex><br> <tex>H_0\,:\, p=p_0,</tex><br> <tex>H_1\,:\, p\neq p_0;</tex><br> <tex>p=0\,:\,0.01\,:\,0.5, \;\; n=5\,:\,1\,:\,70.</tex>
| + | |
| - | ::: <tex>p_0=0.5</tex>; сравнить z-критерии в версиях Вальда и множителей Лагранжа.
| + | |
| - | ::: <tex>p_0=0.25</tex>; сравнить z-критерий в версии множителей Лагранжа и точный критерий.
| + | |
| - | :::<tex>p_0=0.1</tex>; сравнить z-критерий в версии Вальда и точный критерий.
| + | |
| - | | + | |
| - | * <tex>X^n, \;\; X\sim N(\mu,\sigma); </tex><br> <tex>H_0\,:</tex> среднее значение <tex>X</tex> равно нулю,<br> <tex>H_1\,:</tex> среднее значение <tex>X</tex> не равно нулю;<br> <tex>\mu=0\,:\,0.01\,:\,2.</tex>
| + | |
| - | ::: <tex>\sigma=1, \;\; n=5\,:\,1\,:\,70;</tex> сравнить критерии знаков и знаковых рангов.
| + | |
| - | ::: <tex>\sigma=2, \;\; n=5\,:\,1\,:\,70;</tex> сравнить критерий знаковых рангов и одновыборочный t-критерий.
| + | |
| - | ::: <tex>\sigma=1, \;\; n=5\,:\,1\,:\,70;</tex> сравнить одновыборочные t- и z-критерии.
| + | |
| - | ::: <tex>\sigma=1, \;\; n=5\,:\,1\,:\,40;</tex> сравнить одновыборочные t- и перестановочный критерии.
| + | |
| - | | + | |
| - | * <tex>X_1^{n_1}, \;\; X_{1} \sim N(\mu_1, \sigma_1^2),</tex><br> <tex>X_2^{n_2}, \;\; X_{2} \sim N(\mu_2, \sigma_2^2);</tex><br><tex>H_0\,:</tex> средние равны, <br><tex>\;H_1\,:</tex> средние не равны;<br><tex>n_1=30, \;\; \mu_1=0, \;\; \sigma_1=1.</tex>
| + | |
| - | ::: <tex>\mu_2=0\,:\,0.01\,:\,2, \;\; \sigma_2 = 2, \;\; n_2=5\,:\,1\,:\,70,</tex> сравнить версии t-критерия для равных и неравных дисперсий.
| + | |
| - | ::: <tex>\mu_2=0\,:\,0.01\,:\,2, \;\; \sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n_2=30,</tex> сравнить t-критерий для неравных дисперсий и критерий Манна-Уитни-Уилкоксона.
| + | |
| - | ::: <tex>\mu_2=0.5, \;\; \sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n_2=5\,:\,1\,:\,70,</tex> сравнить t- и z-критерии для неравных дисперсий.
| + | |
| - | ::: <tex>\mu_2=0\,:\,0.02\,:\,2, \;\; \sigma_2 = 0.5\,:\,0.02\,:\,2, \;\; n_2=20,</tex> сравнить критерий Манна-Уитни-Уилкоксона и перестановочный критерий с разностью средних в качестве статистики.
| + | |
| - | ::: <tex>\mu_2=0\,:\,0.02\,:\,2, \;\; \sigma_2 = 1, \;\; n_2=5\,:\,1\,:\,40,</tex> сравнить t-критерий для неизвестных равных дисперсий и перестановочный критерий с разностью средних в качестве статистики.
| + | |
| - | | + | |
| - | * <tex>X_1^n, \;\; X_{1} \sim N(0, \sigma_1^2),</tex><br> <tex>X_2^n, \;\; X_{2} \sim N(0, \sigma_2^2);</tex> <br> <tex>H_0\,:\, \mathbb{D}X_{1} = \mathbb{D}X_{2},</tex> <br> <tex>H_1\,:\, \mathbb{D}X_{1} \neq \mathbb{D}X_{2}.</tex>
| + | |
| - | ::: <tex>\sigma_1= 0.5\,:\,0.01\,:\,2, \;\;\sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n=30;</tex> сравнить критерии [[критерий Фишера|Фишера]] и [[критерий Ансари-Брэдли|Ансари-Брэдли]].
| + | |
| - | ::: <tex>\sigma_1= 1, \;\;\sigma_2 = 0.5\,:\,0.01\,:\,2, \;\; n=5\,:\,1\,:\,40;</tex> сравнить критерии [[критерий Фишера|Фишера]] и перестановочный критерий со статистикой Али.
| + | |
| - | ::: <tex>\sigma_1=1, \;\;\sigma_2 = 0.5\,:\,0.05\,:\,2, \;\; n=5\,:\,1\,:\,40,</tex> сравнить критерии [[критерий Ансари-Брэдли|Ансари-Брэдли]] и [[критерий Зигеля-Тьюки|Зигеля-Тьюки]].
| + | |
| - | | + | |
| - | = Анализ устойчивости критериев к нарушению предположений =
| + | |
| - | Требуется исследовать поведение указанного критерия в условиях нарушения лежащих в его основе предположений. Оценить мощность и достигаемый уровень значимости критерия при различных значениях параметров, сделать выводы об устойчивости.
| + | |
| - | | + | |
| - | * Двухвыборочный [[критерий Стьюдента|t-критерий]] для равных дисперсий, нарушение предположения о равенстве дисперсий. <br> <tex>X_1^{n_1}, \;\; X_{1} \sim N(0,1),</tex><br><tex>X_2^{n_2}, \;\; X_{2} \sim N(\mu,\sigma^2);</tex> <br> <tex>H_0\,:\; \mathbb{E}X_{1} = \mathbb{E}X_{2}, </tex> <br> <tex>H_1\,:\; \mathbb{E}X_{1} \neq \mathbb{E}X_{2}.</tex>
| + | |
| - | ::: <tex>\mu=1, \;\; \sigma=0.5\,:\,0.01\,:\,2, \;\; n_1=5\,:\,1\,:\,70, \;\; n_2 = 30.</tex>
| + | |
| - | ::: <tex>\mu = 0\,:\,0.01\,:\,2, \;\; \sigma=0.5\,:\,0.01\,:\,2, \;\; n_1=20, \;\; n_2 = 30.</tex>
| + | |
| - | | + | |
| - | * Одновыборочный [[критерий Стьюдента|t-критерий]], нарушение предположения о нормальности. <br> <tex>X^n, \;\; X \sim p\cdot N(\mu,\sigma^2)+ \left(1-p\right)\cdot F; </tex> <br> <tex>H_0\,:\; \mathbb{E}X=0</tex> <br> <tex>H_1\,:\; \mathbb{E}X\neq0;</tex> <br><tex>\mu=0\,:\,0.01\,:\,2, \;\; n=30.</tex> <br>
| + | |
| - | ::: <tex>F = U\left[-\sqrt{3}+\mu, \sqrt{3}+\mu\right]</tex> — непрерывное равномерное распределение; <tex>\sigma=1, \;\; p=0\,:\,0.01\,:\,1.</tex> <!---брать mu до 1 или sigma больше---> | + | |
| - | ::: <tex>F = C\left(\mu,1\right)</tex> — распределение Коши с коэффициентом сдвига <tex>\mu</tex> и коэффициентом масштаба <tex>1; \;\; \sigma=1, \;\; p=0\,:\,0.01\,:\,1.</tex>
| + | |
| - | ::: <tex>F = \mu + St(3)</tex> — сдвинутое на <tex>\mu</tex> распределение Стьюдента с тремя степенями свободы; <tex>\sigma = \sqrt{3}, \;\; p=0\,:\,0.01\,:\,1.</tex>
| + | |
| - | ::: <tex>F = U\left[-a+\mu, a+\mu\right]</tex> — непрерывное равномерное распределение; <tex>\sigma=1, \;\; p=0.7, \;\; a=0.1\,:\,0.05\,:\,5.</tex>
| + | |
| - | | + | |
| - | * Одновыборочный критерий хи-квадрат для гипотезы о дисперсии, нарушение предположения о нормальности. <br> <tex>X^n, \;\; X \sim p\cdot N(0,\sigma^2)+ \left(1-p\right)\cdot F; </tex> <br> <tex>H_0\,:\; \mathbb{D}X=\sigma_0^2</tex> <br> <tex>H_1\,:\; \mathbb{D}X\neq\sigma_0^2;</tex> <br><tex>p=0\,:\,0.01\,:\,1, \;\; n=50.</tex> <br>
| + | |
| - | ::: <tex>F = St(3)</tex> — распределение Стьюдента с тремя степенями свободы; <tex>\sigma_0^2 = 3, \;\; \sigma^2=1.5\,:\,0.05\,:\,6.</tex>
| + | |
| - | ::: <tex>F = U\left[-\sqrt{3}, \sqrt{3}\right]</tex> — непрерывное равномерное распределение; <tex>\sigma_0 = 1, \;\; \sigma=0.5\,:\,0.01\,:\,2.</tex>
| + | |
| - | ::: <tex>F = \chi^2_2 - 2,</tex> — сдвинутое на 2 распределение хи-квадрат с 2 степенями свободы; <tex>\sigma_0 = 2, \;\; \sigma=1\,:\,0.02\,:\,4.</tex>
| + | |
| - | | + | |
| - | * [[Критерий Фишера]] для проверки равенства дисперсий, нарушение предположения о нормальности. <br> <tex>X_1^{n_1}, \;\; X_{1} \sim p_1\cdot N(0,\sigma_1^2)+ \left(1-p_1\right)\cdot F_1, </tex> <br> <tex> X_2^{n_2},\;\; X_{2} \sim p_2\cdot N(0,\sigma_2^2)+ \left(1-p_2\right)\cdot F_2; </tex> <br> <tex>H_0\,:\, \mathbb{D}X_{1} = \mathbb{D}X_{2},</tex> <br> <tex>H_1\,:\, \mathbb{D}X_{1} \neq \mathbb{D}X_{2}.</tex> <br>
| + | |
| - | ::: <tex>F_1 = U\left[-\sqrt{3}, \sqrt{3}\right]</tex> — непрерывное равномерное распределение; <tex>\sigma_1=1, \;\; \sigma_2=0.2\,:\,0.01\,:\,2, \;\; p_1=0.7, \;\; p_2 = 1, \;\; n_1=5\,:\,1\,:\,70, \;\; n_2=30.</tex>
| + | |
| - | ::: <tex>F_1 = U\left[-\sqrt{3}, \sqrt{3}\right], \;\; F_2 = U\left[-\sigma_2\sqrt{3}, \sigma_2\sqrt{3}\right]</tex> — непрерывные равномерные распределения; <tex>\sigma_1=1, \;\; \sigma_2=0.2\,:\,0.01\,:\,2, \;\; p_1= 1 - p_2=0\,:\,0.01\,:\,1, \;\; n_1=n_2=50.</tex>
| + | |
| - | ::: <tex>F_1 = St(3)</tex> — распределение Стьюдента с тремя степенью свободы; <tex>\sigma_1^2=3, \;\; \sigma_2^2=1.5\,:\,0.05\,:\,6, \;\; p_1=0\,:\,0.01\,:\,1, \;\; p_2 = 1, \;\; n_1=n_2=30.</tex>
| + | |
| - | ::: <tex>F_1 = F_2 = U\left[-3, 3\right]</tex> — непрерывное равномерное распределение; <tex>\sigma_1=1, \;\; \sigma_2=0.5\,:\,0.01\,:\,2, \;\; p_1=p_2 = 0\,:\,0.01\,:\,1, \;\; n_1=n_2=50.</tex>
| + | |
| - | | + | |
| - | * Критерий знаковых рангов Уилкоксона, нарушение предположения о симметричности распределения относительно медианы. <br> <tex>X^n, \;\; X \sim p\cdot N(\mu,1)+ \left(1-p\right)\cdot F; </tex> <br> <tex>H_0\,:\; med X=0</tex> <br> <tex>H_1\,:\; med X\neq0;</tex> <br><tex>\mu=0\,:\,0.01\,:\,2, \;\; p=0\,:\,0.01\,:\,1.</tex> <br>
| + | |
| - | ::: <tex>F = LN(0,1) - 1 + \mu, </tex> где <tex>LN(0,1)</tex> — стандартное логнормальное распределение; <tex>n=50.</tex>
| + | |
| - | ::: <tex>F = \chi^2_4 - \frac{10}{3} + \mu,</tex> где <tex>\chi^2_4</tex> — распределение хи-квадрат с 4 степенями свободы; <tex>n=30.</tex> <!--- можно mu до 1--->
| + | |
| | | | |
| | = Ссылки = | | = Ссылки = |
| | * psad.homework@gmail.com | | * psad.homework@gmail.com |
| - | * [[Статистический анализ данных (курс лекций, К.В.Воронцов)/2016, ММП|Практические задания для студентов ММП ВМК]]
| |
| | * [[Статистический анализ данных (курс лекций, К.В.Воронцов)]] | | * [[Статистический анализ данных (курс лекций, К.В.Воронцов)]] |
| | + | * [[Статистический анализ данных (курс лекций, К.В.Воронцов)/2016, ММП|Практические задания для студентов ММП ВМК (2016 год)]] |
| | <references/> | | <references/> |
| | | | |
1055 химических молекул описаны с помощью 41 признака (число атомов кислорода, нитратных групп, донорных связей с водородом, потенциал ионизации и т.д.); 355 из них биоразложимы. (biodeg.xlsx)
Собраны данные мониторинга сейсмической активности в польских угольных шахтах столбовой системы разработки. При сейсмической опасности существует серьёзный риск обрушения; в этом случае необходимо отозвать рабочих или использовать направленные взрывы для нейтрализации напряжения породы. Для каждого измерения известен бинарный индикатор сейсмической опасности — наличия в следующую восьмичасовую смену сейсмических толчков с энегрией выше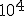 
Джоулей. (seismic.xlsx)
Данные собраны из переписи населения США 1990 года, отчёта ФБР о преступности за 1995 год и опроса сотрудников полиции LEMAS за 1990 год. По 2215 округам собрана статистика преступлений и 125 демографических показателей. (crimes.xlsx)
Полихлорированные дифенилы — органические соединения, активно использовавшиеся в промышленности до 1970 годов, когда была показана их токсичность. Накопление ПХБ в организме приводит к подавлению иммунитета, провоцирует развитие рака, поражений печени, почек, нервной системы, кожи, способствуют развитию детской патологии. Из-за накопления ПХБ в озёрах США некоторые виды рыб в некоторых областях запрещены к употреблению в пищу. Для своевременного обновления таких запретов необходимо периодически проводить мониторинг ПХБ. К сожалению, существует 209 различных разновидностей ПХБ, концентрация каждой из которых измеряется отдельным тестом.
Для 69 видов рыбы известны концентрации семи соединений ПХБ (в миллионных долях), а также суммарная концентрация всех разновидностей ПХБ, их токсическая эквивалентность (TEQ) и суммарная токсическая эквивалентность образца, определяемая также вкладом диоксинов и фуранов. (pcb.txt)
